Работа при перемещении в потенциальном поле вдоль любого замкнутого контура равна нулю.

Последнее утверждение может служить еще одной формулировкой потенциальности поля. Формула Стокса применительно к напряженности электрического поля принимает вид

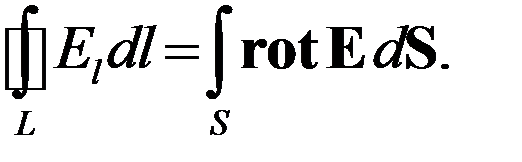
Поскольку в электростатическом поле циркуляция вектора E вдоль любого замкнутого контура равна нулю, отсюда следует следующая формулировка потенциальности поля:

.

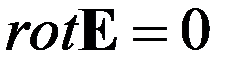Из соотношений (2) и (7) следует еще одна важная формула. Она связывает потенциал и напряженность электростатического поля:

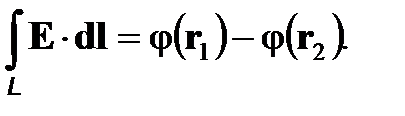(10)

Ее можно переписать в следующем виде

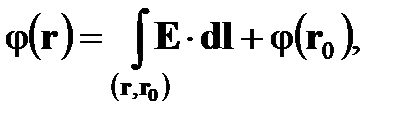(11)

где r₀–радиус-вектор точки, потенциал поля которой считается заданным. В случае конечного числа точечных зарядов в качестве такой точки обычно принимают бесконечно удаленную, и потенциал ее приравнивают нулю. В этой формуле вместо кривой, вдоль которой ведется интегрирование, указаны радиус-векторы начальной (r) и конечной (r₀) точек, так как в потенциальном поле значение такого интеграла определяется только положением начальной и конечной точек относительно системы зарядов.

& В п. 2 раздела I было показано, что если линейный интеграл вектора A вдоль всякой замкнутой кривой равен нулю, то

Adr=d (r),

т. е. вектор A является потенциальным и. представим градиентом некоторого скаляра. Аналогично из соотношения (11) следует, что

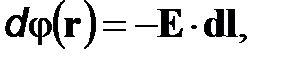(12)

где появление знака «минус» обусловлено тем, что в соотношении (11) зафиксирована конечная точка с радиус-вектором r₀, и интеграл является функцией исходной точки с радиус-вектором r.

По другому:

Работа сил поля по перемещению заряда 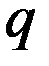из точки 1 в точку 2 определяется по формуле

.

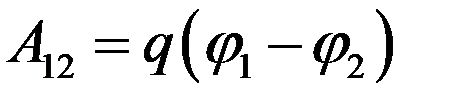В СГСЭ за единицу разности потенциалов принимается разность потенциалов между двумя такими точками, что при перемещении 1 СГСЭ заряда из одной точки в другую электрическое поле совершает работу в 1 эрг. Эта единица не получила специального названия. Практической единицей является вольт. 1 вольт есть разность потенциалов между такими точками, что при перемещении 1Кл из одной точки в другую электрическое поле совершает работу в 1Дж. Имеем

1В=1Дж/1Кл = 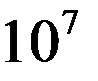эрг/ 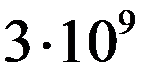СГСЭ ед. заряда=1/300 CГСЭ ед. потенциала.

Если расстояние между точками 1 и 2 мало, то

.

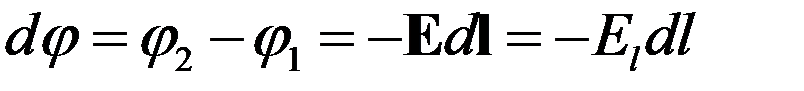Вспоминая определение производной скалярной функции по направлению имеем отсюда

.

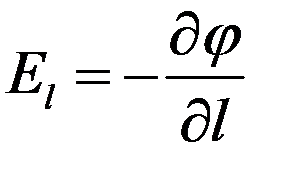Производная по направлению связана с градиентом следующей формулой векторного анализа

.

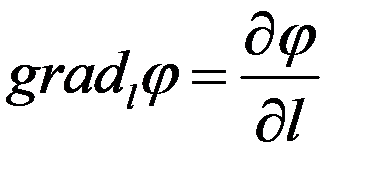Отсюда находим

.

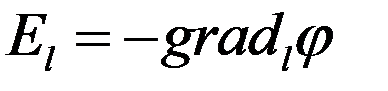Равенство проекций должно иметь место при любом выборе направления .

Поэтому напряженность поля можно представить в виде

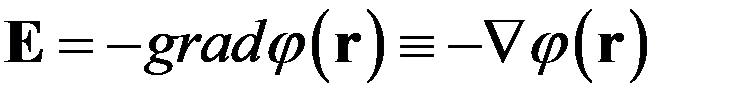 . (13)

Это важное соотношение позволяет рассчитать напряженность электростатического поля по известному как функция координат потенциалу. Здесь нужно отметить следующий существенный момент. В общем случае напряженность электрического поля E определяется тремя функциями координат E(r)_x, E_y(r), E_z(r). Потенциальность же электростатического поля накладывает на эти компоненты столь сильное ограничение, что для описания электростатического поля достаточно одного скалярного поля (r):

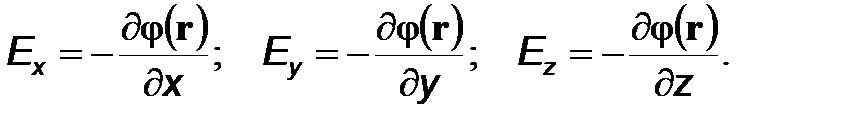(13 a)

Потенциал как функция координат имеет разрыв в местах расположения точечных зарядов, т. к. у соответствующего слагаемого первой суммы формулы (9) обращается в нуль знаменатель. В областях пространства, в которых нет точечных и линейных зарядов, потенциал остается конечным и непрерывным. Непрерывность его следует из формулы (12): всюду, где конечна напряженность электрического поля, непрерывен потенциал. А E конечна всюду, где нет точечных и линейных зарядов.