Пространственный промежуток. Лоренцево сокращение длины.
Понятия «РАЗМЕР ТЕЛА», «промежуток времени между событиями» не имеют абсолютного характера и различны для различных систем отсчета.
Рассмотрим тонкий стержень, который покоится в системе 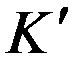 . Его длина равна
. Его длина равна
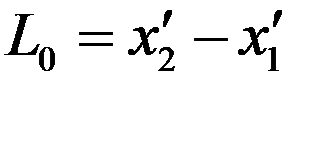 . (1)
. (1)
Измерения координат конца масштаба в 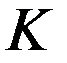 проводятся в один и тот же момент времени
проводятся в один и тот же момент времени 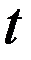 , что естественно, так как масштаб движется. Имеем
, что естественно, так как масштаб движется. Имеем
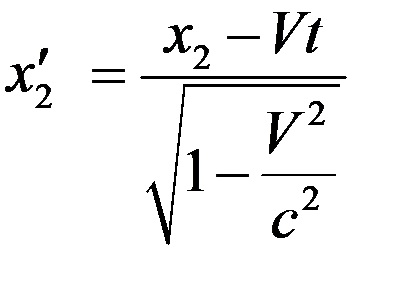 , (2)
, (2)
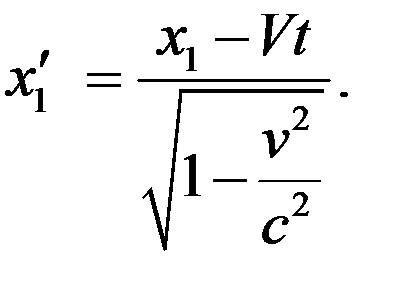 . (3)
. (3)
Отсюда получаем
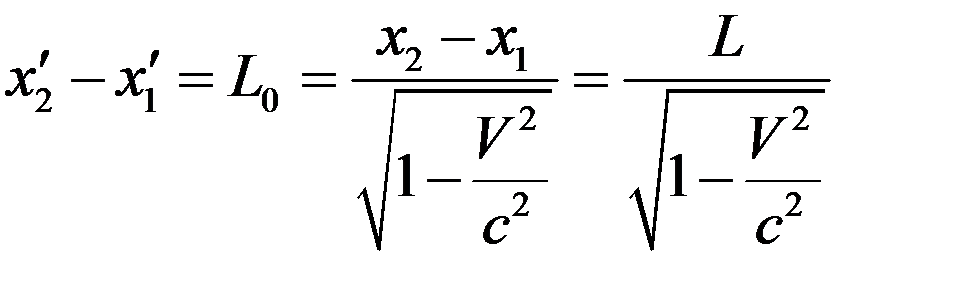 . (4)
. (4)
Т.о., находим
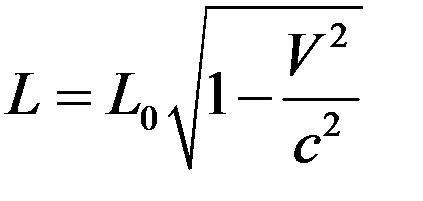 . (5)
. (5)
Т.о., длина масштаба по отношению к системе 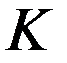 меньше, чем его собственная длина. Это сокращение длины наз. лоренцевым сокращением. Поэтому утверждение «расстояние между двумя точками пространства равно
меньше, чем его собственная длина. Это сокращение длины наз. лоренцевым сокращением. Поэтому утверждение «расстояние между двумя точками пространства равно 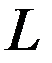 »не имеет смысла без указания к какой системе отсчета отнесена эта величина.
»не имеет смысла без указания к какой системе отсчета отнесена эта величина.
Собственное время объекта
Пусть в 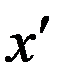 в системе
в системе 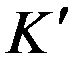 происходит физический процесс в течение промежутка времени
происходит физический процесс в течение промежутка времени
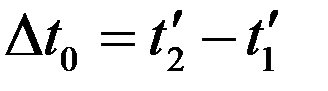 . (6)
. (6)
Тогда в системе отсчета 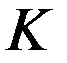 имеем
имеем
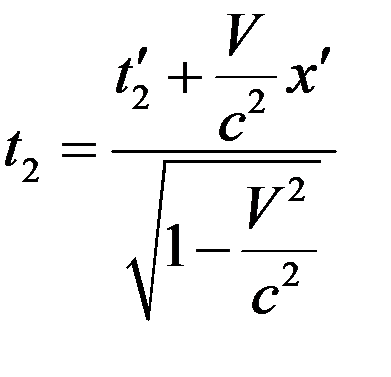 , (7)
, (7)
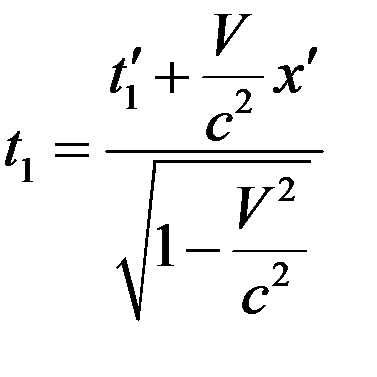 . (8)
. (8)
Отсюда находим
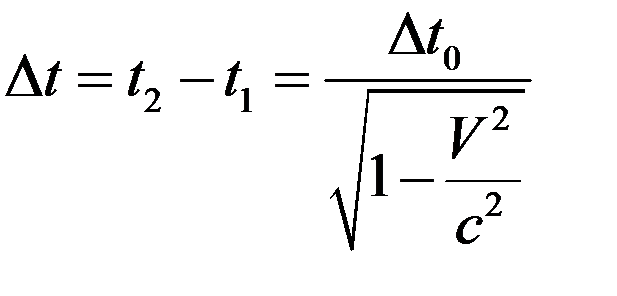 . (9)
. (9)
Формула (9) была проверена экспериментально многими способами.
В космических лучах наблюдается распад 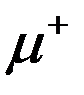 - мезона и
- мезона и 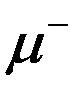 - мезона соответственно на позитрон и два нейтрино и на электрон и два нейтрино. При этом наблюдается распад как заторможенных до остановки
- мезона соответственно на позитрон и два нейтрино и на электрон и два нейтрино. При этом наблюдается распад как заторможенных до остановки 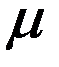 -мезонов с временем жизни
-мезонов с временем жизни 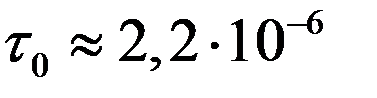 с, так и на лету, когда они движутся со скоростью, близкой к скорости света. Времена жизни связаны соотношением
с, так и на лету, когда они движутся со скоростью, близкой к скорости света. Времена жизни связаны соотношением
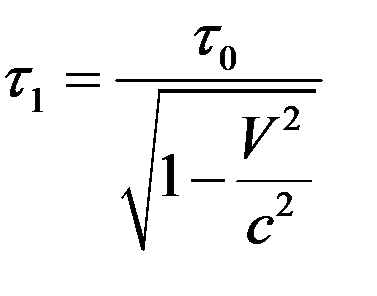 , (10)
, (10)
где 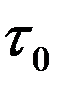 - время жизни покоящихся
- время жизни покоящихся 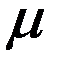 -мезонов, а
-мезонов, а 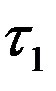 - - время жизни движущихся
- - время жизни движущихся 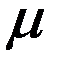 -мезонов. Если бы время жизни не зависело от скорости они бы пролетали путь
-мезонов. Если бы время жизни не зависело от скорости они бы пролетали путь
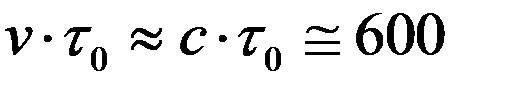 м.
м.
В действительности мюоны проходят путь около 20 км. Такому пробегу отвечает время жизни
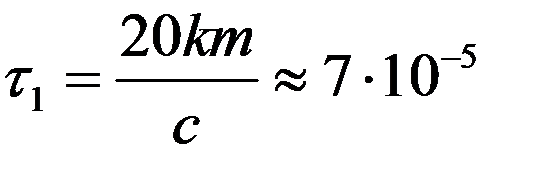 с
с 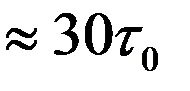 .
.
Релятивистское изменение времени жизни здесь большой и, так сказать, вполне реальный эффект.
Парадокс близнецов
Пусть мы наблюдаем из некоторой инерциальной системы отсчета движущиеся произвольным образом относительно нас часы. В каждый момент времени можно ввести неподвижно связанную с часами систему координат,котораябудет инерциальной. Тогда промежуток времени 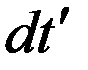 по движущимся часам будет связан с промежутком времени по неподвижным часам
по движущимся часам будет связан с промежутком времени по неподвижным часам 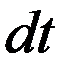 формулой
формулой
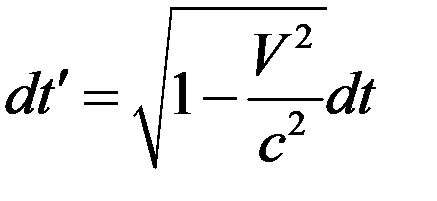 . (1)
. (1)
Интегрируя это соотношение, имеем
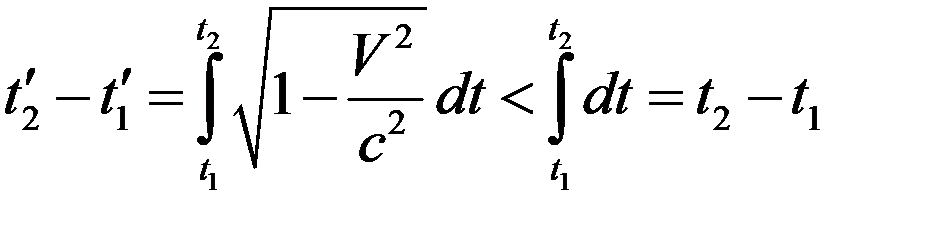 . (2)
. (2)
Отсюда видно, что собственное время всегда меньше.
Преобразование скорости
Имеем
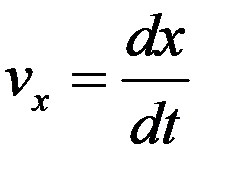 , (1)
, (1)
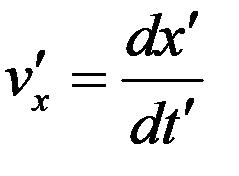 . (2)
. (2)
Запишем формулы обратного преобразования
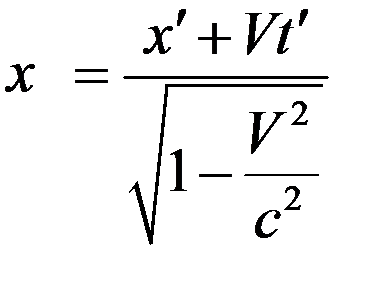 , (3)
, (3)
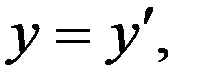 (4)
(4)
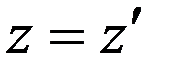 , (5)
, (5)
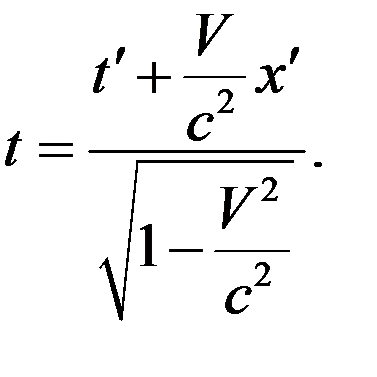 (6)
(6)
Возьмем дифференциал от этих соотношений. Получим
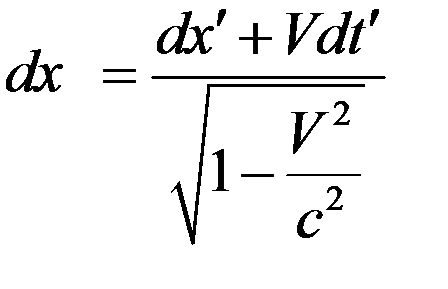 . (7)
. (7)
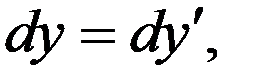 (8)
(8)
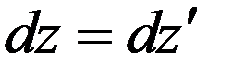 ,(9)
,(9)
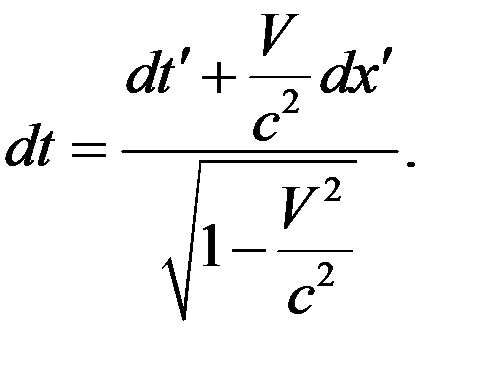 (10)
(10)
Отсюда получаем
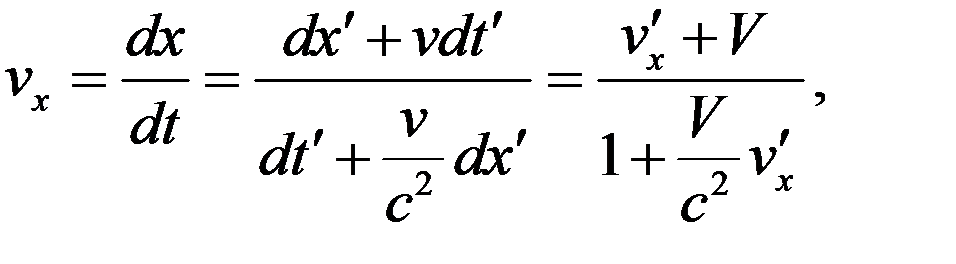 (11)
(11)
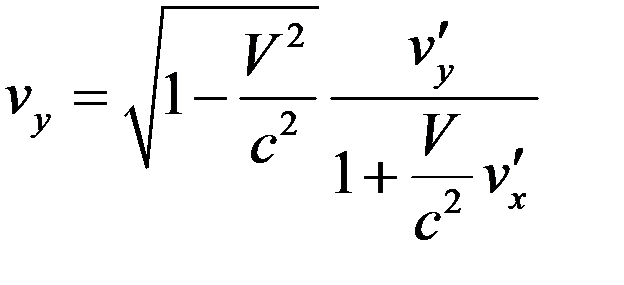 , (12)
, (12)
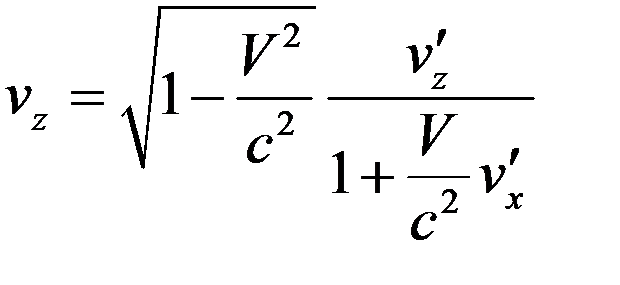 . (13)
. (13)
В формулах, выражающих «штрихованные» скорости через «нештрихованнные» изменяются штрихи и знак 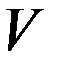 у скорости.
у скорости.
Рассмотрим пример.
Пусть в 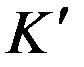 частица движется со скоростью света
частица движется со скоростью света  . Тогда в системе отсчета
. Тогда в системе отсчета 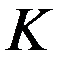 ее скорость равна
ее скорость равна
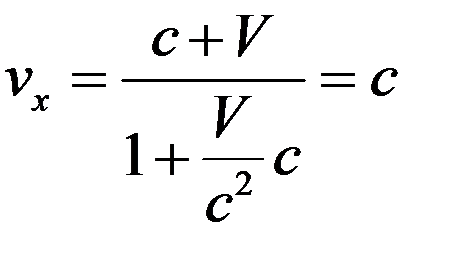
как и должно быть!
Инварианты. Интервал между событиями.
В теории относительности много величин –инвариантов, которые не зависят от выбора системы отсчета. Одна из них – скорость распространения взаимодействия в вакууме. Важным инвариантом является интервал между событиями
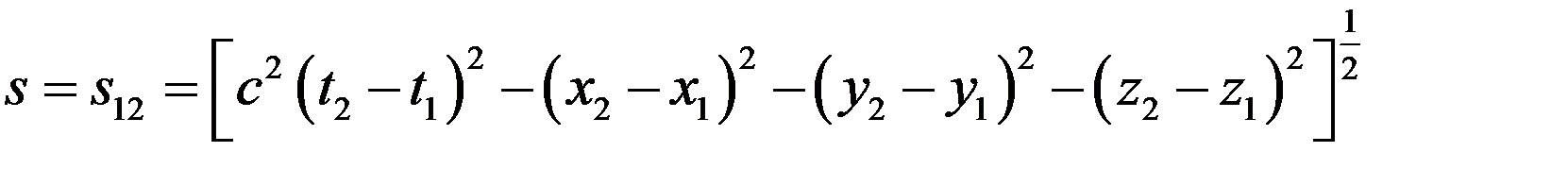 (1)
(1)
Прямым вычислением можно показать, что
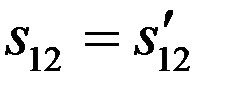 .
.
Поэтому утверждение «два физических события разделены интервалом 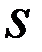 » справедливо во всех инерциальных системах отсчета.
» справедливо во всех инерциальных системах отсчета.
