Электростатическая теорема Гаусса-Остроградского.
Механика
1. Основные понятия классической механики. Скорость, ускорение. Угловая скорость. Угловое ускорение.
2.Законы Ньютона. Закон сохранения импульса. Центр масс системы частиц.
3.Работа силы. Мощность. Кинетическая и потенциальная энергия. Полная энергия механической системы.
4.Принцип относительности Эйнштейна. Преобразования Лоренца.
5.Лоренцево сокращение длины. Собственное время объекта. Парадокс близнецов.
6.Преобразование скорости в СТО.
7.Интервал между событиями. Принцип наименьшего действия. Функция Лагранжа в СТО.
8.Энергия и импульс свободной частицы.
9.Уравнения Максвелла. Токи смещения. Материальные уравнения.
10.Электромагнитные волны в диэлектрике.
11.Явление электромагнитной индукции. Правило Ленца. Основной закон электромагнитной индукции. Трактовка Максвелла.
12.Закон Кулона. Работа в электростатическом поле. Потенциальность электростатического поля. Потенциал системы точечных зарядов.
Электростатическая теорема Гаусса-Остроградского.
14. Закон Био- Савара-Лапласа.
15. Сила Лоренца. Сила Ампера.
16. Основные положения и понятия МКТ. Агрегатные состояния вещества.
17. Основное уравнение МКТ(уравнение Клаузиуса).
18. Уравнение Менделеева-Клапейрона. Закон Дальтона. Изопроцессы.
19. Средняя энергия молекул. Закон о равномерном распределении кинетической энергии по степеням свободы.
20. Закон Максвелла распределения молекул идеального газа по скоростям.
21. Барометрическая формула. Распределение Больцмана.
22. Явления переноса в газах. Закон Фика. Закон Фурье. Сила внутреннего трения.
23. Реальные газы. Уравнение Ван-дер-Ваальса.
24. Термодинамическая система. Равновесные и неравновесные состояния. Равновесный процесс. Внутренняя энергия, работа и теплота.
25. Первое начало термодинамики. Теплоёмкость и внутренняя энергия идеального газа. Уравнение Майера.
26. Адиабатический процесс. Работа, совершаемая идеальным газом при различных процессах.
27. Микросостояние и макросостояние. Статистический вес макросостояния. Энтропия. Свойства энтропии. Теорема Нернста.
28. Второе начало термодинамики. Проблема тепловой смерти Вселенной.
29. Фотоэффект. Уравнение Эйнштейна. Давление света. Вынужденное излучение. Лазеры.
30. Гипотеза де Бройля. Уравнение Шредингера.
31. Принцип суперпозиции. Физический смысл квадрата модуля пси-функции. Стандартные условия.одномерной
32. Квантование энергии. Энергия частицы в бесконечно глубокой
одномерной потенциальной яме. Описание физических величин в квантовой механике.
33. Теория Бора атома водорода. Принцип неопределённости.
34. Состав и характеристики атомного ядра. Ядерные силы. Энергия связи атомных ядер. Синтез легких ядер.
35. Радиоактивность. Закон радиоактивного распада. Ядерные реакции.
Материальной точкой называется тело, размерами которого в данной задаче можно пренебречь. Произвольное макроскопическое тело можно мысленно разбить на совокупность материальных точек. Тогда изучение движения сводится к изучению движения материальных точек. В механике сначала изучают движение одной материальной точки, а затем переходят к изучению движения системы материальных точек.
Абсолютно твёрдым телом наз. тело, которое не может деформироваться и при всех условиях расстояние между двумя частицами этого тела остаётся постоянным.
Абсолютно упругое тело – тело, деформация которого подчиняется закону Гука, а после прекращения действия внешних сил принимает свои первоначальные размеры.
Абсолютно неупругое тело – тело, полностью сохраняющее деформированное состояние после прекращения действия внешних сил .
 Тело отсчёта – произвольно выбранное тело, относительно которого определяется положение других движущихся или покоящихся тел.
Тело отсчёта – произвольно выбранное тело, относительно которого определяется положение других движущихся или покоящихся тел.
Система отсчёта – совокупность тела отсчёта, связанной с ним системы координат и синхронизованных между собой часов.
Уравнения движения частицы
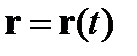 ,
,
или в компонентах
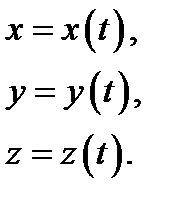
Траекторией наз. линия, описываемая движущейся частицей относительно выбранной системы отсчёта.
Траектории движений одного и того же тела в разных система отсчёта могут быть различными.
Вектор перемещения
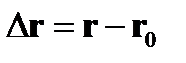 .
.
Скорость
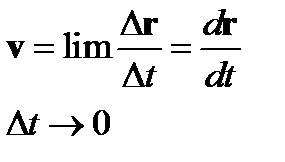 .
.
Модуль скорости
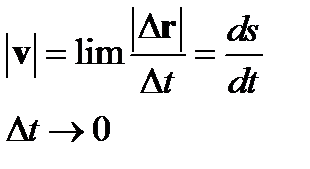 .
.
Длина пути
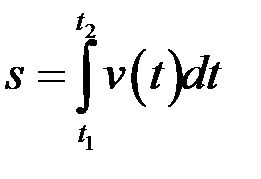 .
.
Ускорение
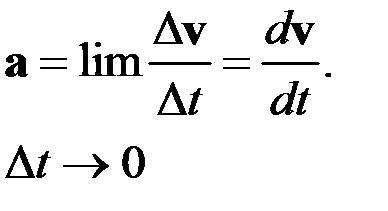
Полное ускорение можно представить в виде
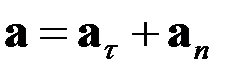 .
.
Тангенциальная составляющая
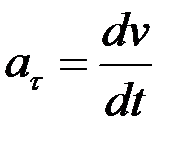
характеризует быстроту изменения скорости по модулю и направлена по касательной к траектории.
Нормальная составляющая
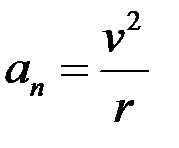
характеризует быстроту изменения скорости по направлению и направлена к центру кривизны траектории.
Вращательным движением твёрдого тела наз. движение, при котором все точки тела движутся по окружностям, центры которых лежат на одной прямой, называемой осью вращения.
Угловая скорость
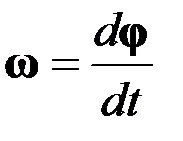 .
.
Вектор  направлен вдоль оси вращения по правилу правого винта, также как и вектор
направлен вдоль оси вращения по правилу правого винта, также как и вектор 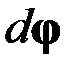 .
.
Угловое ускорение
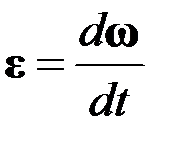 .
.
Имеют место формулы

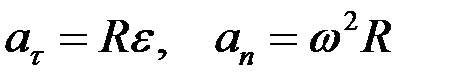 .
.
Первый закон Ньютона
Частица сохраняет состояние покоя или равномерного прямолинейного движения, пока воздействие со стороны других тел не заставит её изменить это состояние.
Инерциальной системой отсчёта наз. система отсчёта, относительно которой свободная частица движется равномерно и прямолинейно.
Инертностью тел наз. свойство, заключающееся в том, что тела оказывают сопротивление изменению их скорости.
Инерционные и гравитационные свойства определяет масса тела.
Инертная и гравитационная массы равны друг другу.
Второй закон Ньютона
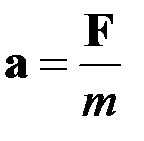
Или
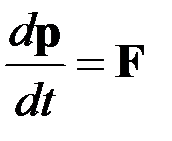 .
.
Здесь
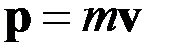
Импульс.
Второй закон Ньютона справедлив только в инерциальных системах отсчёта.
Третий закон Ньютона
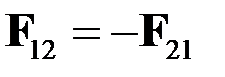 .
.
Закон сохранения импульса
Импульс замкнутой системы
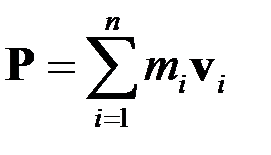
сохраняется.Это фундаментальный закон природы. Он является следствием однородности пространства. При параллельном переносе замкнутой системы в пространстве её физические свойства не изменяются.
Центр масс системы частиц
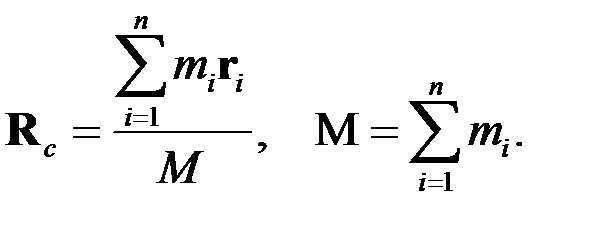
Центр масс системы движется как частица, в которой сосредоточена масса всей системы и на которую действует сила, равная сумме всех внешних сил, действующих на систему
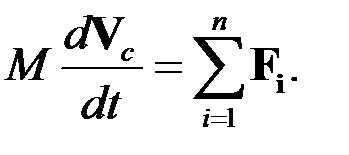
Работа силы
Элементарная работа.
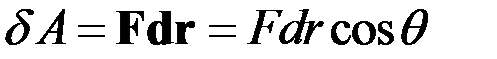 .
.
Работа
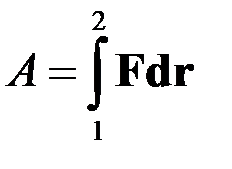 .
.
Мощность
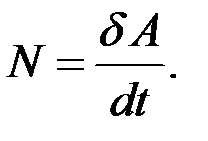
Кинетическая энергия
Приращение кинетической энергии частицы на элементарном перемещении равно элементарной работе на том же перемещении
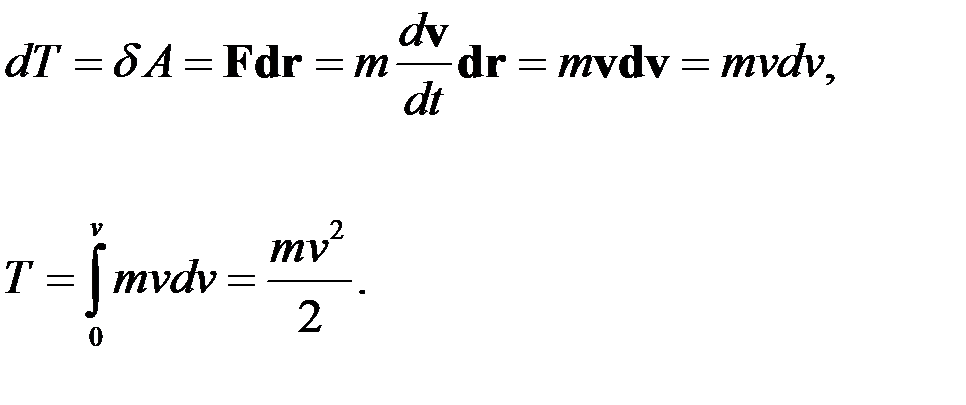
Кинетическая энергия неодинакова в разных инерциальных системах отсчета.
Потенциальной энергией наз. механическая энергия системы частиц, определяемая их взаимным расположением и характером сил взаимодействия между ними.
Потенциальным полем наз. поле, в котором работа, совершаемая силами поля при перемещении тела из одного положения в другое зависит только от начального и конечного положений.
Консервативной силой наз. сила, работа которой при перемещении частицы из одного положения в другое зависит только от начального и конечного положений частицы. Выполняются формулы
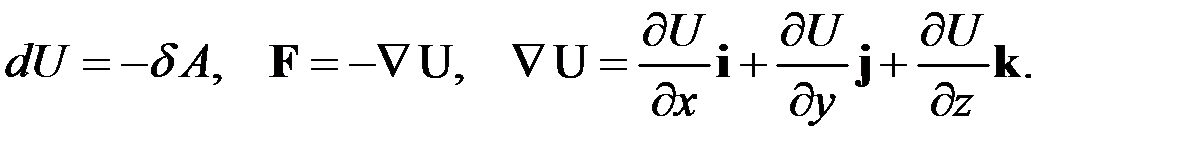
Полной энергией механической системы наз.
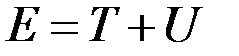 .
.
Преобразования Лоренца
Инерциальная система отсчета – это такая система, в которой материальная точка, не взаимодействующая с какими-либо другими телами, движется равномерно и прямолинейно или покоится.
Принцип относительности Эйнштейна
1. Законы природы инвариантны (неизменны) при переходе от одной инерциальной системы отсчета к другой
2. Существует предельная скорость распространения взаимодействия, равная в пустоте скорости света
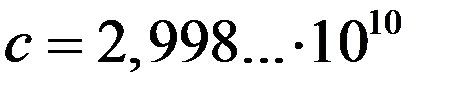 см/c.
см/c.
Вообще любые взаимодействия между телами в пустоте распространяются со скоростью света.
Принцип предельной скорости выражает утверждение о том, что скорость распространения взаимодействия в пустоте носит универсальный характер и связана непосредственно со свойствами пространства и времени, а не с физической природой взаимодействия.
Пусть имеются две системы отсчета 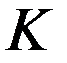 и
и 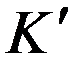 , причем вторая система отсчета перемещается относительно первой в направлении их общей оси
, причем вторая система отсчета перемещается относительно первой в направлении их общей оси 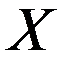 и
и 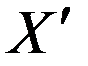 со скоростью
со скоростью 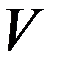 . Выберем за начало отсчета времени
. Выберем за начало отсчета времени 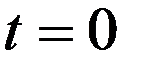 тот момент времени, в который начала координат совпадают.
тот момент времени, в который начала координат совпадают.
Пусть в момент времени 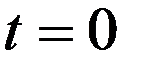 из начала координат начала распространяться сферическая электромагнитная волна . В системе
из начала координат начала распространяться сферическая электромагнитная волна . В системе 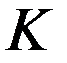 уравнениеволновогофронтаимеет вид
уравнениеволновогофронтаимеет вид
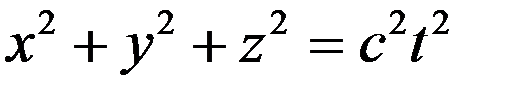 . (1)
. (1)
Согласно принципу относительности Эйнштейна имеем в системе 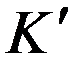
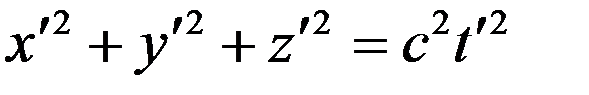 . (2)
. (2)
Из однородности пространства и времени вытекает требование линейности преобразования. В силу линейности преобразования
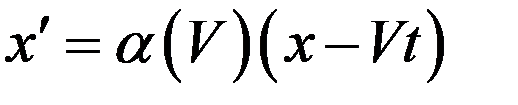 . (3)
. (3)
Далее очевидно
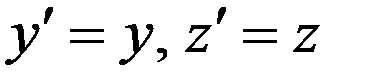 . (4)
. (4)
Формула преобразования времени в силу свойства линейности имеет вид
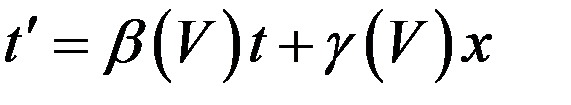 . (5)
. (5)
Здесь коэффициенты 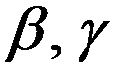 зависят от скорости
зависят от скорости 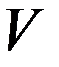 . Далее, очевидно, имеем
. Далее, очевидно, имеем
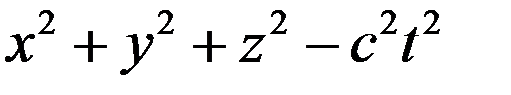 =
= 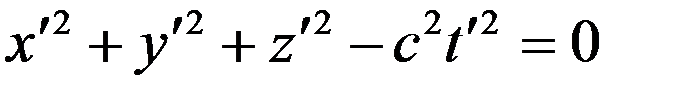 . (7)
. (7)
Поэтому
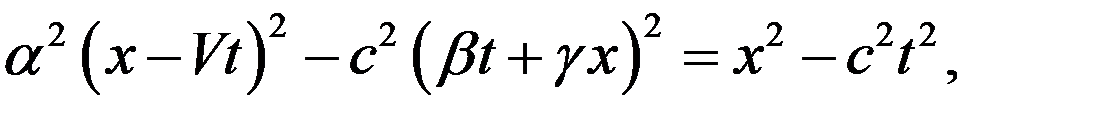 (8)
(8)
Далее мы должны приравнять коэффициенты при 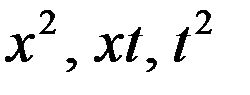 слева к соответствующим коэффициентам справа. Получим
слева к соответствующим коэффициентам справа. Получим
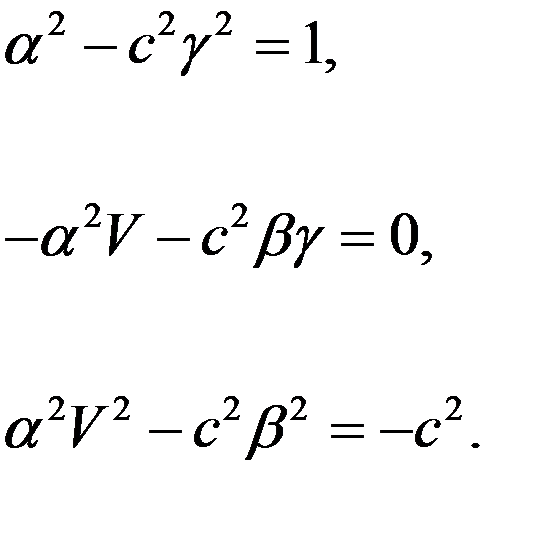 (9)
(9)
Решая алгебраическую систему уравнений (9), учитывая при этом принцип соответствия, получим
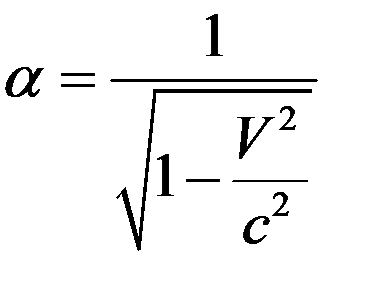 . (10)
. (10)
Далее находим
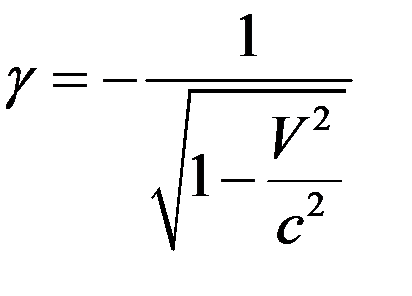
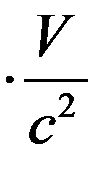 , (11)
, (11)
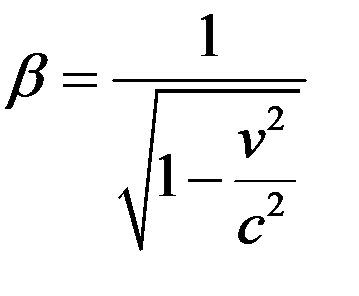 . (12)
. (12)
Итак, получили
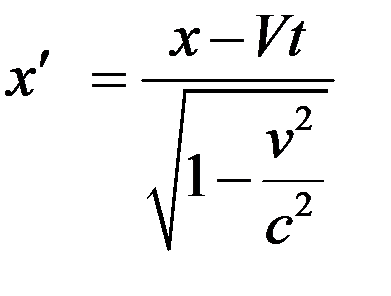 . (13)
. (13)
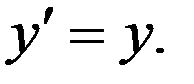 (14)
(14)
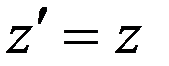 , (15)
, (15)
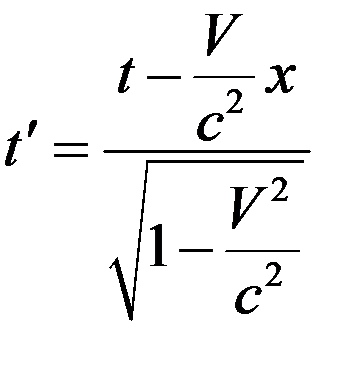 . (16)
. (16)
Из формул (13)-(16) можно получить формулы обратного преобразования.
Но эти формулы получаются и путем следующих рассуждений.
Системы 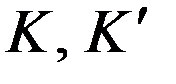 эквивалентны. Поэтому мы могли повторить предыдущие рассуждения, взяв за исходную систему
эквивалентны. Поэтому мы могли повторить предыдущие рассуждения, взяв за исходную систему 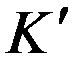 . При этом должны получиться те же формулы, но со скоростью относительного движения
. При этом должны получиться те же формулы, но со скоростью относительного движения 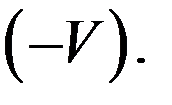
Формулы обратного преобразования имеют вид
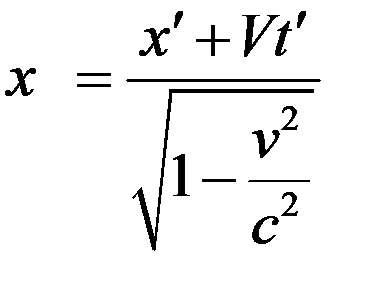 , (17)
, (17)
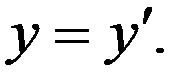 (18)
(18)
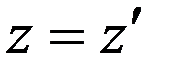 , (19)
, (19)
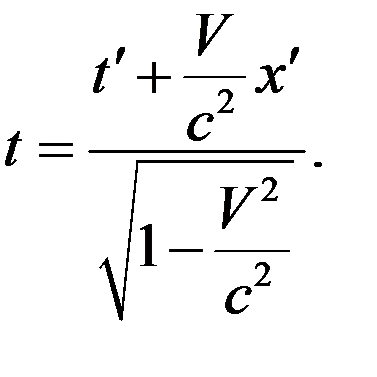 (20)
(20)
Собственное время объекта
Пусть в 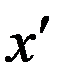 в системе
в системе 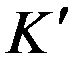 происходит физический процесс в течение промежутка времени
происходит физический процесс в течение промежутка времени
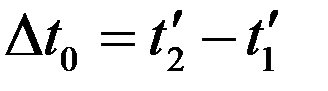 . (6)
. (6)
Тогда в системе отсчета 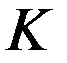 имеем
имеем
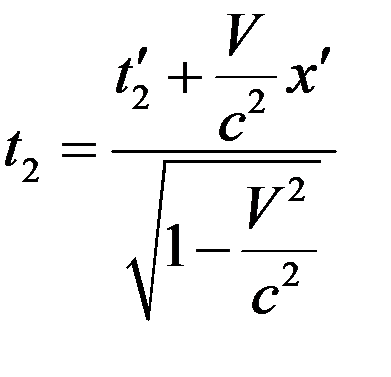 , (7)
, (7)
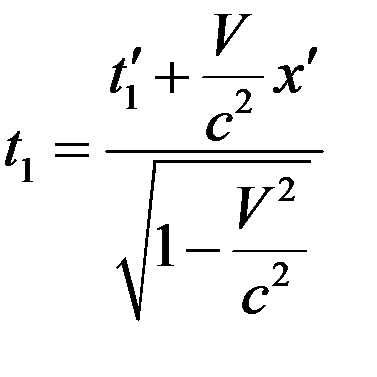 . (8)
. (8)
Отсюда находим
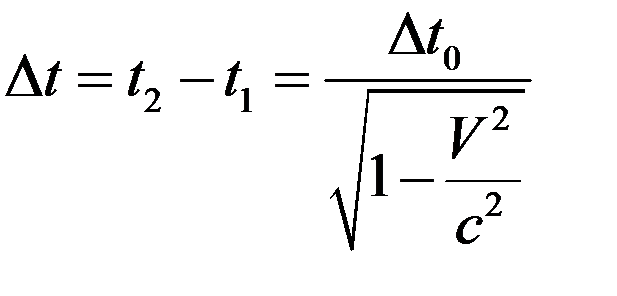 . (9)
. (9)
Формула (9) была проверена экспериментально многими способами.
В космических лучах наблюдается распад 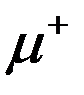 - мезона и
- мезона и 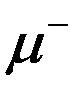 - мезона соответственно на позитрон и два нейтрино и на электрон и два нейтрино. При этом наблюдается распад как заторможенных до остановки
- мезона соответственно на позитрон и два нейтрино и на электрон и два нейтрино. При этом наблюдается распад как заторможенных до остановки 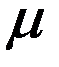 -мезонов с временем жизни
-мезонов с временем жизни 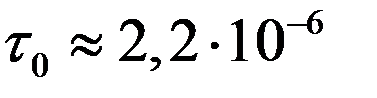 с, так и на лету, когда они движутся со скоростью, близкой к скорости света. Времена жизни связаны соотношением
с, так и на лету, когда они движутся со скоростью, близкой к скорости света. Времена жизни связаны соотношением
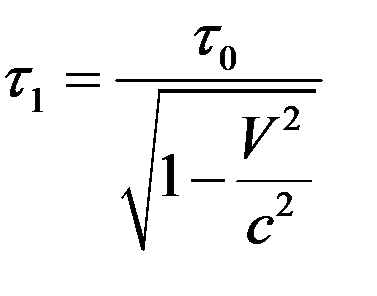 , (10)
, (10)
где 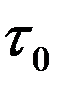 - время жизни покоящихся
- время жизни покоящихся 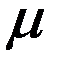 -мезонов, а
-мезонов, а 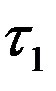 - - время жизни движущихся
- - время жизни движущихся 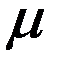 -мезонов. Если бы время жизни не зависело от скорости они бы пролетали путь
-мезонов. Если бы время жизни не зависело от скорости они бы пролетали путь
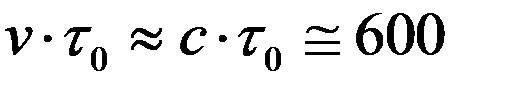 м.
м.
В действительности мюоны проходят путь около 20 км. Такому пробегу отвечает время жизни
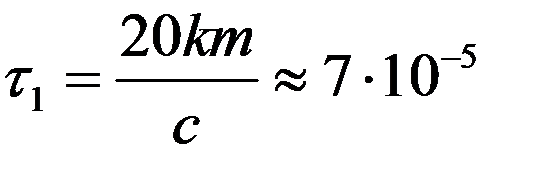 с
с 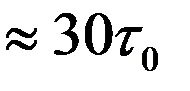 .
.
Релятивистское изменение времени жизни здесь большой и, так сказать, вполне реальный эффект.
Парадокс близнецов
Пусть мы наблюдаем из некоторой инерциальной системы отсчета движущиеся произвольным образом относительно нас часы. В каждый момент времени можно ввести неподвижно связанную с часами систему координат,котораябудет инерциальной. Тогда промежуток времени 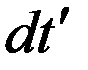 по движущимся часам будет связан с промежутком времени по неподвижным часам
по движущимся часам будет связан с промежутком времени по неподвижным часам 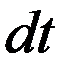 формулой
формулой
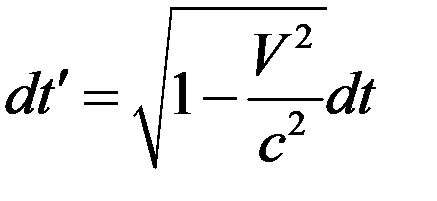 . (1)
. (1)
Интегрируя это соотношение, имеем
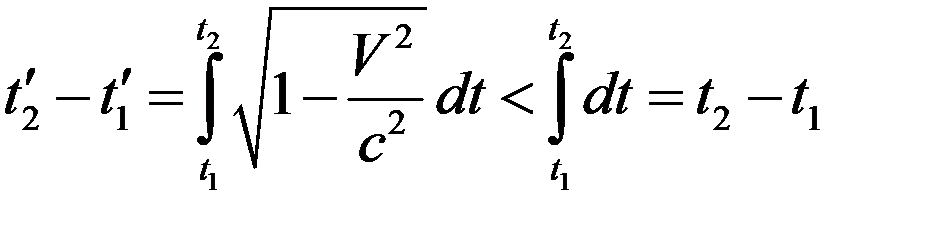 . (2)
. (2)
Отсюда видно, что собственное время всегда меньше.
Преобразование скорости
Имеем
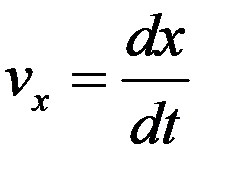 , (1)
, (1)
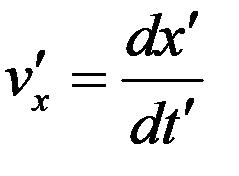 . (2)
. (2)
Запишем формулы обратного преобразования
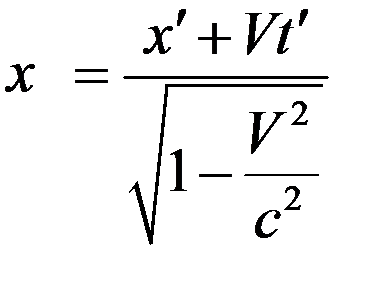 , (3)
, (3)
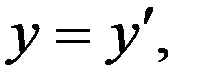 (4)
(4)
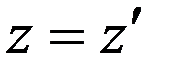 , (5)
, (5)
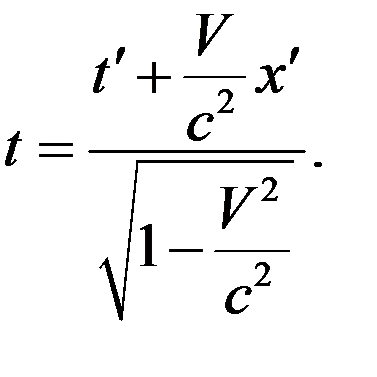 (6)
(6)
Возьмем дифференциал от этих соотношений. Получим
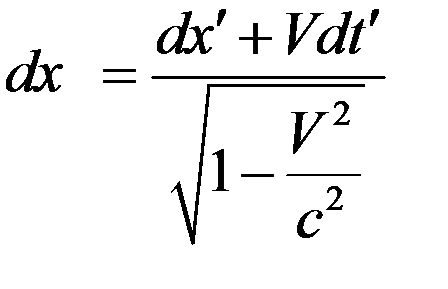 . (7)
. (7)
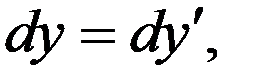 (8)
(8)
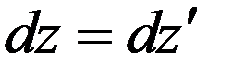 ,(9)
,(9)
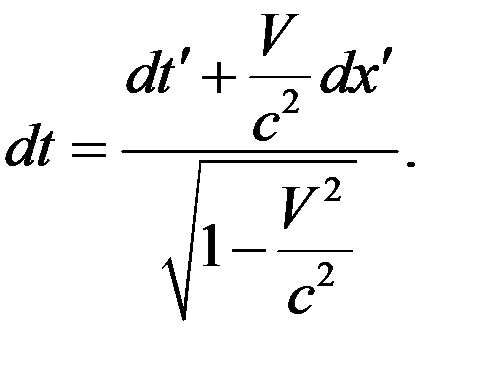 (10)
(10)
Отсюда получаем
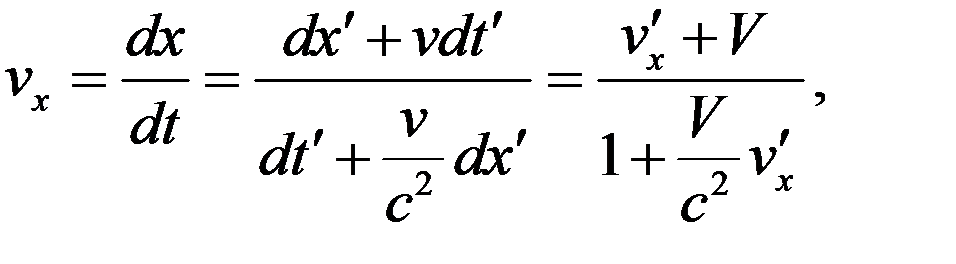 (11)
(11)
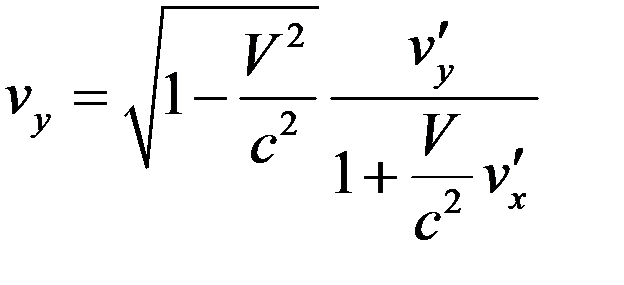 , (12)
, (12)
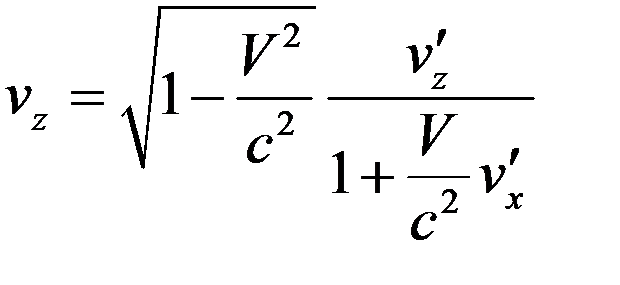 . (13)
. (13)
В формулах, выражающих «штрихованные» скорости через «нештрихованнные» изменяются штрихи и знак 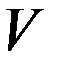 у скорости.
у скорости.
Рассмотрим пример.
Пусть в 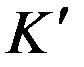 частица движется со скоростью света
частица движется со скоростью света  . Тогда в системе отсчета
. Тогда в системе отсчета 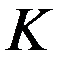 ее скорость равна
ее скорость равна
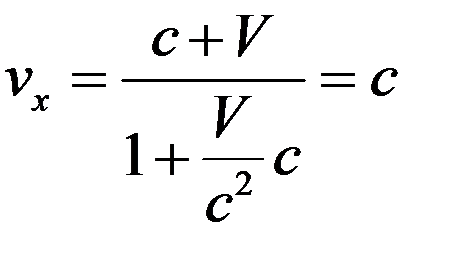
как и должно быть!
Инварианты. Интервал между событиями.
В теории относительности много величин –инвариантов, которые не зависят от выбора системы отсчета. Одна из них – скорость распространения взаимодействия в вакууме. Важным инвариантом является интервал между событиями
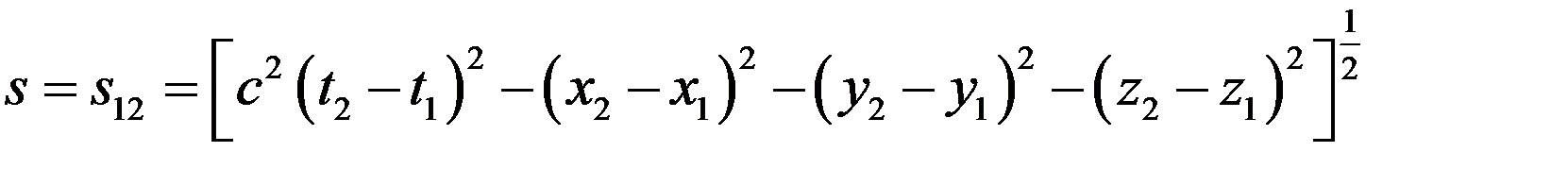 (1)
(1)
Прямым вычислением можно показать, что
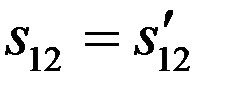 .
.
Поэтому утверждение «два физических события разделены интервалом 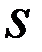 » справедливо во всех инерциальных системах отсчета.
» справедливо во всех инерциальных системах отсчета.
Уравнения Максвелла
Суммируя результаты теоретических и экспериментальных исследований, запишем систему четырех основных фундаментальных уравнений электродинамики в дифференциальной форме
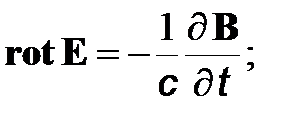 (2)
(2)
divB=0; (3)
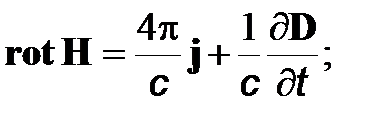 (4)
(4)
divD=4pr. (5)
Систему уравнений (2)–(5) называют системой уравнений Максвелла (уравнения (2), (3) составляют так называемую первую пару уравнений Максвелла, а уравнения (4), (5) - вторую пару уравнений Максвелла).
Отметим, что уравнение непрерывности , выражающее фундаментальный закон сохранения заряда, вытекает из второй пары уравнений Максвелла. Чтобы убедиться в этом, необходимо взять дивергенцию от обеих частей (4) и далее воспользоваться уравнением (5). Данное следствие уравнений Максвелла представляется вполне естественным, так как уравнение непрерывности непосредственно использовалось при поиске выражения для плотности тока смещения
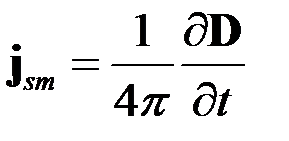 .
.
Дифференциальные уравнения (2)–(5) должны быть дополнены граничными условиями, которым должны удовлетворять величины E, H, D, B на границе раздела двух сред. Легко установить, что поверхностная плотность токов смещения всегда равна нулю. Поэтому совокупность граничных условий имеет вид
D2n–D1n=4ps; (6)
B2n=B1n; (7)
E2t=E1t; (8)
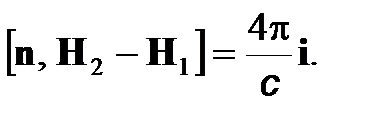 (9)
(9)
Здесь единичный вектор n, перпендикулярный к границе раздела, проведен из среды 1 в среду 2, s–поверхностная плотность заряда, i–поверхностная плотность тока проводимости.
Итак, источниками электрического поля являются либо электрические заряды, либо изменяющиеся во времени магнитные поля. Источниками же магнитного поля являются либо электрические токи (движущиеся заряды), либо переменные электрические поля.
Отсутствие симметрии уравнений относительно электрического и магнитного полей обусловлено предполагаемым отсутствием магнитных зарядов в природе ( неоднократные попытки обнаружить магнитные заряды до настоящего времени не увенчались успехом).
Интегральная форма уравнений Максвелла имеет вид
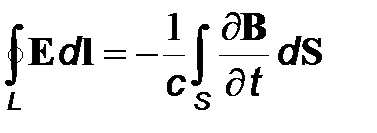 , (10)
, (10)
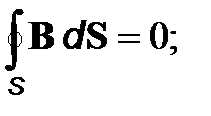 (11)
(11)
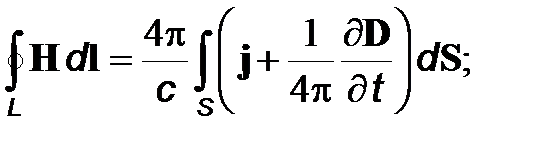 (12)
(12)
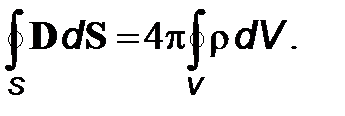 (13)
(13)
Отметим, что уравнение (12) представляет собой обобщение теоремы о циркуляции вектора напряженности магнитного поля. В уравнении (12) учтено, что магнитное поле создается как токами проводимости, так и токами смещения.
В интегральной форме уравнения Максвелла обладают наибольшей общностью, так как в этой форме уравнений не предполагается непрерывность входящих в уравнения величин. Эти уравнения выполняются и в тех случаях, когда существуют поверхности разрыва.
Система уравнений Максвелла не является полной. Например, система уравнений (2)-(5), записанная в координатной форме, содержит 8 скалярных уравнений, связывающих 16 величин. При использовании декартовой системы координат это следующие величины: Ex, Ey, Ez, Dx, Dy, Dz, Bx, By, Bz, Hx, Hy, Hz, jx, jy, jz,r.
Поэтому уравнения Максвелла необходимо дополнить так называемыми материальными уравнениями. Эти уравнения должны характеризовать свойства среды, в которой возбуждается электромагнитное поле. Необходимо сразу подчеркнуть, что одна и та же среда может характеризоваться различными материальными уравнениями в зависимости от величины параметров электромагнитного поля. Материальные уравнения должны быть получены, вообще говоря, на основе молекулярной теории среды. Возможен и феноменологический подход, опирающийся на обобщение опытных данных. В сложных случаях получение материальных уравнений может представлять собой серьезную современную научную проблему.
Как показывают, в частности, экспериментальные исследования, материальные уравнения наиболее просты в изотропных неферромагнитных и несегнетоэлектрических средах при условии незначительного изменения электромагнитного поля за характерные времена собственных внутримолекулярных колебаний и на протяжении межмолекулярных расстояний и при условии малой величины электромагнитного поля по сравнению с характерным собственным полем молекул среды (такие условия обычно выполняются при решении многих технических задач). Эти материальные уравнения имеют вид
D=eE, (14)
B=mH, (15)
j=lE. (16)
Здесь e, m, l - диэлектрическая проницаемость, магнитная проницаемость, электропроводность среды.
Теперь к основной системе уравнений Максвелла добавляется 9 скалярных материальных уравнений, и общее число уравнений становится равным 17. Некоторая математическая переопределенность общей системы уравнений обусловлена тем обстоятельством, что уравнение (3) при соответствующем выборе начального условия вытекает из уравнения (2). Действительно, возьмем дивергенцию от обеих частей уравнения (2). Тогда получим
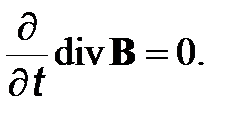 (17)
(17)
Уравнение (17) означает, что если divB=0 в начальный момент времени, то она будет равна нулю и в последующие моменты времени. Поэтому уравнение (3) с формальной точки зрения фактически лишь накладывает ограничение на вид начального условия для B.
Отметим, что в анизотропной среде, например, закон Ома принимает вид
ji=likEk. (18)
В формуле (18), как обычно, подразумевается суммирование по повторяющемуся индексу, lik–тензор электропроводности. В анизотропных средах и в сильных полях вместо (18) нередко используют следующее более общее уравнение:
ji=likEk+giknEkEn+ziknmEkEnEm. (19)
В курсе теоретической физики система уравнений Максвелла в вакууме формулируется как инвариантная система, служащая для определения четырехмерного тензора второго ранга–тензора электромагнитного поля. С помощью данного тензора можно описывать электромагнитное поле инвариантным способом (в смысле теории относительности). В рамках такого описания отчетливо проявляется следующее свойство: электрическое и магнитное поле являются составляющими единого электромагнитного поля. Выделить определенные электрическое и магнитное поле можно только в том случае, если выбрана инерциальная система отсчета. Можно находить инерциальные системы отсчета, в которых данное электромагнитное поле имеет наиболее простой вид. Например, в определенных случаях можно найти такую инерциальную систему отсчета, в которой в нуль обращается напряженность электрического поля, либо напряженность магнитного поля.
Электромагнитная индукция
Трактовка Максвелла
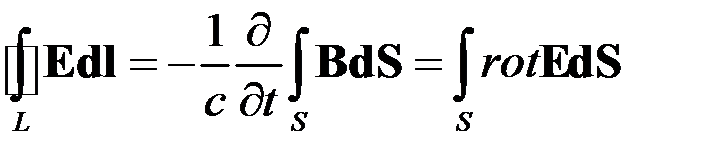 .
.
Отсюда вытекает дифференциальная форма закона электромагнитной индукции
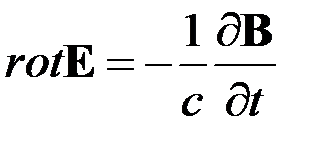 .
.
Закон Кулона
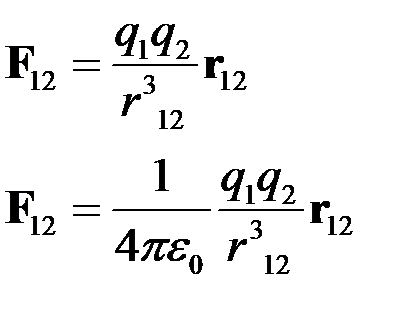
Здесь 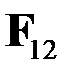 - cила, действующая на заряд 2 со стороны заряда1. Вектор
- cила, действующая на заряд 2 со стороны заряда1. Вектор 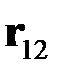 направлен от заряда 1 к заряду 2.
направлен от заряда 1 к заряду 2.
Точечный заряд – тело , размерами которого можно пренебречь в данной задаче.
Закон Кулона справедлив для точечных зарядов.
Электрические силы являются дальнодействующими и очень сильными.
Закон Кулона справедлив для покоящихся зарядов.
Закон Кулона проверен вплоть до расстояний порядка 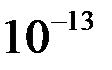 см.
см.
Кулоновская сила является ньютоновской
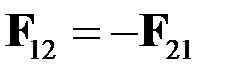
Сила взаимодействия двух зарядов не изменяется при наличии третьего заряда, а также при наличии большего числа зарядов. Это утверждение, проверенное опытным путём носит название принципа суперпозиции.
Электрический заряд-величина инвариантная, она не изменяется при движении заряда.
Электрически заряд аддитивен: заряд любой системы равен сумме зарядов его составляющих.
Работа при перемещении заряда в электростатическом поле не зависит от пути, по которому перемещается заряд, и определяется только величиной перемещаемого заряда и разностью потенциалов поля в исходной и конечной точках.
Телесный угол
Как известно,
плоский угол ÐAOB–это часть плоскости, ограниченная лучами OA и OB, а радианной мерой угла называется отношение длины соответствующей дуги окружности к радиусу r:
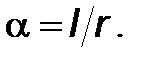 (3)
(3)
| R |
| S |
| O |
| W |
телесный угол есть часть пространства, заключенная внутри одной полости некоторой конической поверхности (с замкнутой направляющей), и за меру телесного угла принимают отношение площади, вырезаемой телесным углом на сфере с центром в вершине телесного угла, к квадрату радиуса R сферы
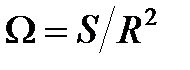 (4)
(4)
Телесный угол измеряют в стерадианах (ср).
Все пространство вокруг любой данной точки составляет полный телесный угол. Его величина W=4  R2/ R2=4
R2/ R2=4  ср.
ср.
| R |
| O |
| n |
| a |
| dS |
| dSn |
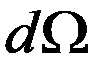 =dSn/R2, где dSn–проекция площадки dS на плоскость, перпендикулярную радиус-вектору R, проведенному из точки О в центр этой площадки. Из рис. видно, что dSn=dScos
=dSn/R2, где dSn–проекция площадки dS на плоскость, перпендикулярную радиус-вектору R, проведенному из точки О в центр этой площадки. Из рис. видно, что dSn=dScos 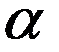 , где
, где 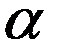 –угол между вектором R и нормалью n к площадке dS:
–угол между вектором R и нормалью n к площадке dS: 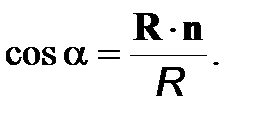 (5)
(5)
Элемент телесного угла тогда при cos 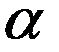 ³0 представляется в виде
³0 представляется в виде
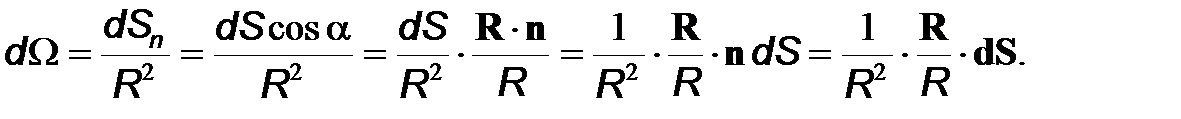 (6)
(6)
Закон Био-Савара-Лапласа
Магнитная индукция движущегося со скоростью v заряда q, радиус-вектор которого в данный момент есть r¢, в точке с радиус-вектором r определяется соотношением вида
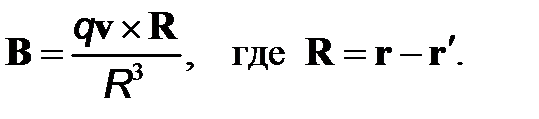 (1)
(1)
В общем случае эта формула, должна содержать коэффициент пропорциональности, зависящий от системы единиц. Этот коэффициент пропорциональности принят равным единице в СГСМ. В СИ он равен 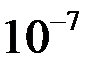 Гн/м (точно) и записывается в виде
Гн/м (точно) и записывается в виде 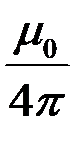 . Коэффициент
. Коэффициент 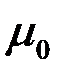 называется магнитной постоянной. В СГС (симметричной системе Гаусса) коэффициент пропорциональности в формуле (1) равен 1/c.
называется магнитной постоянной. В СГС (симметричной системе Гаусса) коэффициент пропорциональности в формуле (1) равен 1/c.
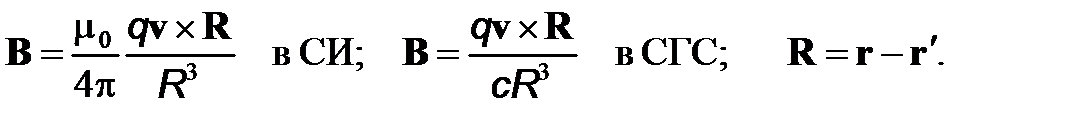 (2)
(2)
Электрический ток представляет собой поток заряженных частиц, и потому также создает магнитное поле. Если средняя скорость заряженных частиц в малом объеме 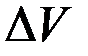 равна u, а их счетная концентрация равна n, их суммарный заряд в указанном объеме равен
равна u, а их счетная концентрация равна n, их суммарный заряд в указанном объеме равен 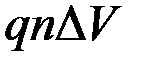 . Ввиду малости
. Ввиду малости 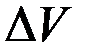 считаем этот заряд точечным, поэтому магнитную индукцию этого заряда записываем в СГСМ по формуле (1):
считаем этот заряд точечным, поэтому магнитную индукцию этого заряда записываем в СГСМ по формуле (1):
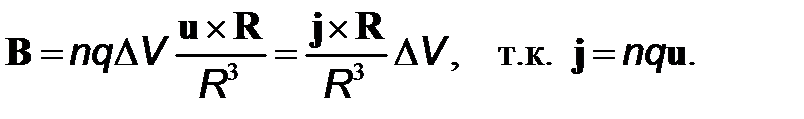
Бесконечно малый (физически) объем dV создает магнитную индукцию
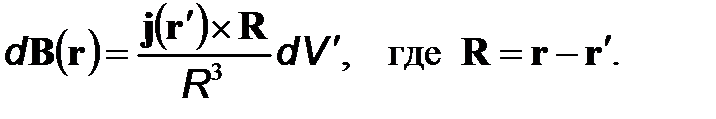
Конечный объем проводника, согласно принципу суперпозиции магнитных полей, создает поле (в СГСМ)
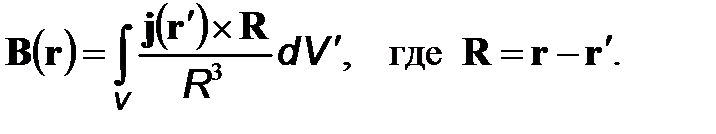 (3)
(3)
Эта формула носит название закона Био–Савара–Лапласа для объемных токов.
Если ток течет по проводам, а магнитная индукция рассчитывается на расстояниях, больших по сравнению с поперечными размерами проводов, это выражение можно преобразовать к иному, более удобному для расчетов виду. Учтём, что
jdV=j∆Sdl=j(∆Sdl)=(j∆S)dl=Idl, (4)
где dl–длина отрезка провода, т. е. объема dV; dl–соответствующий этому отрезку провода вектор, ∆S–площадь поперечного сечения проводника, нормаль которой направлена в ту же сторону, куда и вектор dl. Здесь принято во внимание, что векторы j и dl параллельны и что j∆S представляет собой силу тока в проводнике в направлении, соответствующем направлению вектора dl. В результате приходим еще к одной формуле, выражающей закон Био–Савара–Лапласа, но уже для линейных токов. Для элемента тока бесконечно малой длины
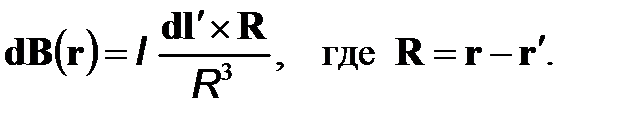 (5)
(5)
Для провода конечной длины
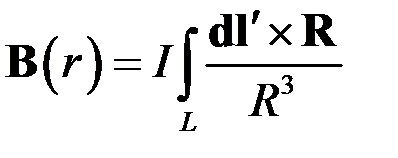 .
.
Фотоэффект
Чтобы объяснить распределение энергии в спектре равновесного теплового излучения, достаточно, как показал Планк, допустить, что свет испускается только отдельными порциями  .
.
Здесь  -частота,
-частота,  =
=  эрг
эрг  с –постоянная Планка.
с –постоянная Планка.
Фотоэлектрическим эффектом наз. испускание электронов из твердых и жидких тел под действием света. Для объяснения фотоэффекта достаточно предположить, что свет поглощается такими же порциями  . В этой связи Эйнштейн выдвинул гипотезу, что свет распространяется в виде дискретных частиц, названных впоследствии фотонами. Эти частицы, однако, существенно отличаются от частиц, рассматриваемых в классической физике. Энергия фотона определяется его частотой
. В этой связи Эйнштейн выдвинул гипотезу, что свет распространяется в виде дискретных частиц, названных впоследствии фотонами. Эти частицы, однако, существенно отличаются от частиц, рассматриваемых в классической физике. Энергия фотона определяется его частотой
 . (1)
. (1)
Фотон движется со скоростью света  и имеет массу покоя, равную нулю. Для таких частиц
и имеет массу покоя, равную нулю. Для таких частиц
 (2)
(2)
В векторной форме
 . (3)
. (3)
Фотон движется в направлении распространения электромагнитной волны.
С помощью представления о фотонах легко получить выражение для давления света (давление света было экспериментально обнаружено Лебедевым). Пусть на поглощающую свет поверхность падает поток фотонов, летящих по нормали к поверхности. Если плотность фотонов равна  , на единицу поверхности падает в единицу времени
, на единицу поверхности падает в единицу времени  фотонов. При поглощении каждый фотон сообщает стенке импульс
фотонов. При поглощении каждый фотон сообщает стенке импульс  . Умножив
. Умножив  на
на  , получим импульс, сообщаемый в единицу времени единице поверхности, т.е. давление света на стенку
, получим импульс, сообщаемый в единицу времени единице поверхности, т.е. давление света на стенку
 (4)
(4)
Произведение  равно энергии фотонов, заключённых в единице объема, т.е. плотности электромагнитной энергии. Отражаясь от стенки, фотон сообщает ей импульс
равно энергии фотонов, заключённых в единице объема, т.е. плотности электромагнитной энергии. Отражаясь от стенки, фотон сообщает ей импульс  . Поэтому для отражающей поверхности давление будет равно 2
. Поэтому для отражающей поверхности давление будет равно 2  .
.
Для объяснения фотоэффекта Эйнштейн предложил уравнение

Здесь  - работа выхода – наименьшая энергия, которую необходимо сообщить электрону, чтобы удалить его из твердого или жидкого тела. Положив кинетическую энергию равной 0, получим из этого соотношения наименьшую частоту, при которой возможен фотоэффект (красная граница фотоэффекта). Простейший фотоэлемент представляет собой хорошо откаченную колбу, на часть внутренней поверхности которой нанесён тонкий слой металла, являющийся катодом. Выбиваемые светом электроны долетают до анода и тем самым замыкают анодную цепь, по которой протекает фототок. Для повышения чувствительности иногда колбу фотоэлемента заполняют каким-либо газом, не реагирующим с веществом фотокатода. Выбитые из катода электроны на своем движении к аноду ионизируют атомы газа. При этом заметно увеличивается фототок.
- работа выхода – наименьшая энергия, которую необходимо сообщить электрону, чтобы удалить его из твердого или жидкого тела. Положив кинетическую энергию равной 0, получим из этого соотношения наименьшую частоту, при которой возможен фотоэффект (красная граница фотоэффекта). Простейший фотоэлемент представляет собой хорошо откаченную колбу, на часть внутренней поверхности которой нанесён тонкий слой металла, являющийся катодом. Выбиваемые светом электроны долетают до анода и тем самым замыкают анодную цепь, по которой протекает фототок. Для повышения чувствительности иногда колбу фотоэлемента заполняют каким-либо газом, не реагирующим с веществом фотокатода. Выбитые из катода электроны на своем движении к аноду ионизируют атомы газа. При этом заметно увеличивается фототок.
Гипотеза де Бройля
Луи де Бройль в 1924 году выдвинул идею о том, что микрочастицы обладаю
