Закон Дальтона для смеси газов

На практике чаще встречаются не чистые газы, а их смеси. Компоненты смеси занимают один и тот же объем и имеют одинаковую температуру. Концентрация смеси равна сумме концентраций компонентов смеси, т. е.

.

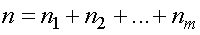Тогда по формуле (4.5) давление смеси равно

.

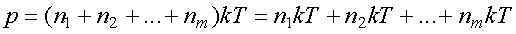Введем обозначения:

,

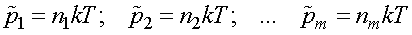где 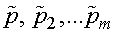- парциальные давления.

Парциальным давлением называется давление, которое производит на стенки сосуда данная компонента смеси. Тогда давление смеси равно

Формула (4.6) представляет собой закон Дальтона. Давление смеси газов равно сумме парциальных давлений.

Изопроцессы

Состояние идеального газа определяется тремя параметрами: p - давление, V - объем и T - термодинамическая температура. Изменение хотя бы одного параметра приводит к новому состоянию. Для двух различных состояний уравнение Клапейрона - Менделеева имеет вид

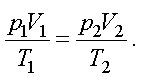
Переход системы из одного состояния в другое называется процессом. Изопроцессом называется процесс, при котором один из параметров остается постоянным. Существует три изопроцесса, законы которых легко получить из уравнения (4.1).

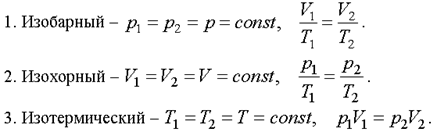
Эти частные законы позволяют связать конечные параметры с начальными.

Молекулярно-кинетический смысл абсолютной температуры

C точки зрения молекулярно-кинетической теории молекулы нагретого тела находятся в хаотическом движении. Причем, чем выше температура T, тем больше средняя кинетическая энергия 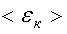хаотического движения молекул .

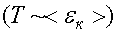Связь между средней кинетической энергией поступательного движения молекулы и абсолютной температурой дается формулой

где k - постоянная Больцмана, .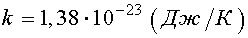

Следовательно, абсолютная температура есть мера средней кинетической энергии поступательного движения молекулы.

Формула (4.7) позволяет выяснить смысл абсолютного нуля: 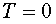, если 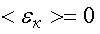. Т. е. абсолютный нуль - это температура, при которой прекращается всякое хаотическое движение молекул.

Давление может быть выражено через среднюю кинетическую энергию поступательного движения молекулы. Если воспользоваться формулами (4.5) и (4.7), то получим

Уравнение (4.8) называется основным уравнением молекулярно-кинетической теории.

Давление идеального газа равно двум третям средней кинетической энергии поступательного движения молекул, заключенных в единице объема.

Формулы (4.7) и (4.8) учитывают только кинетическую энергию поступательного движения молекул. Однако, наряду с поступательным движением возможны также вращательное и колебательное движение, поэтому вводится понятие числа степеней свободы.

Число степеней свободы

Числом степеней свободы механической системы называется число независимых координат, полностью определяющих положение системы в пространстве.

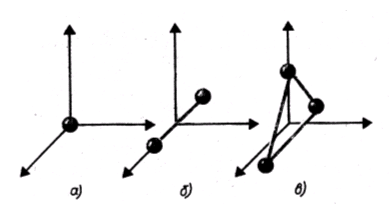
Рис.4.1

На рис. 4.1 показаны одноатомная, двухатомная и трехатомная молекулы. Одноатомную молекулу можно представить как материальную точку. Для определения положения точки в пространстве нужно три координаты, т. е. три степени свободы поступательного движения (i = 3).

Молекулу двухатомного газа в первом приближении можно рассматривать как совокупность двух жестко связанных материальных точек. Эта молекула кроме трех степеней свободы поступательного движения имеет две степени свободы вращательного движения (i = 5). Вращение вокруг оси, проходящей через оба атома, не учитывается.

Трехатомная молекула с жесткими связями имеет 6 степеней свободы: 3 - поступательного и 3 - вращательного движения (i = 6).

В классической физике принят постулат о равномерном распределении энергии по степеням свободы. На каждую степень свободы любого вида движения приходится энергия, равная 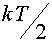. Таким образом, средняя энергия одной молекулы равна