Закон био - савара - лапласа

Три французских ученых в 1820 г. открыли закон, который позволяет рассчитать вектор магнитной индукции, созданный проводником с током. Также можно вычислять напряженность магнитного поля 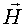, которая связана с вектором магнитной индукции 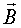соотношением (2.33).

Закон Био - Савара - Лапласа записывается для элемента тока. Элементом тока называется вектор, модуль которого равен произведению силы тока в проводнике на длину малого отрезка этого проводника, а направление совпадает с направлением силы тока - .

Закон Био - Савара - Лапласа в векторной форме формулируется следующим образом.

Вектор магнитной индукции, созданный элементом тока, пропорционален векторному произведению элемента тока на радиус-вектор, проведенный от элемента в точку наблюдения, и обратно пропорционален кубу расстояния от элемента тока до точки наблюдения (рис. 2.11)

Направление вектора определяется по правилу векторного произведения двух векторов и , т. е. перпендикулярен плоскости, в которой лежат перемножаемые вектора, и направлен по правилу правого винта.

Рис.2.11

На рис. 2.11 показана линия магнитной индукции. По касательной к этой линии направлен вектор . Модуль вектора определяется по закону Био - Савара - Лапласа в скалярной форме

где α - угол между векторами и .

Для напряженности магнитного поля можно записать аналогичные формулы

Изолированный элемент с током создать невозможно. Ток, который создает магнитное поле, всегда течет по проводникам конечных размеров. Поэтому далее надо применять принцип суперпозиции и векторно суммировать (интегрировать) или , созданные всеми элементами тока ,

Магнитное поле в центре кругового тока

С помощью закона Био - Савара - Лапласа и принципа суперпозиции найдем напряженность магнитного поля в центре витка с током I радиуса R (рис. 2.12) (виток перпендикулярен чертежу).

Рис.2.12

В этом случае все элементы проводника перпендикулярны радиусу и , т. е. . Расстояние всех элементов провода до центра одинаково и r = R. Поэтому формула (2.37) примет следующий вид

.

Применим принцип суперпозиции.

Все элементы тока создают магнитное поле одинакового направления, перпендикулярно плоскости витка, поэтому от векторного интегрирования можно перейти к скалярному

,

где - длина окружности.

Окончательно получим формулу для вычисления напряженности магнитного поля в центре кругового тока

Магнитная индукция равна

Напомним, что для вакуума μ = 1.

Направление векторов 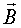и 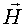нужно находить по правилу правого винта (рис. 2.12) с учетом того, что и .

Магнитное поле прямого тока

Применяя закон Био - Савара - Лапласа и принцип суперпозиции, можно найти напряженность магнитного поля прямого тока. Запишем без вывода конечный результат для проводника конечной длины (рис. 2.13).

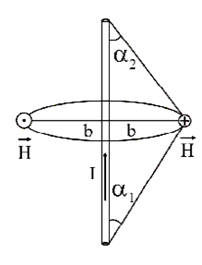
Рис.2.13

Введем следующие обозначения: I - сила тока в проводнике, b - кратчайшее расстояние от точки наблюдения до проводника, α₁ и α₂ - углы между отрезком проводника и линией, соединяющей концы отрезка с точкой наблюдения.

Напряженность магнитного поля, созданного конечным прямым проводником с током, равна

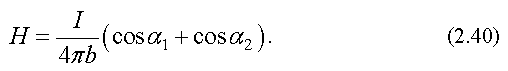
Направление вектора 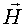определяется по правилу правого винта. Вектор, направленный за чертеж, изображается крестиком 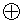. Вектор, направленный к нам - точкой . Линия напряженности представляет собой окружность.

Для бесконечно длинного проводника 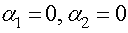и 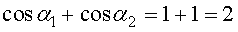. Напряженность магнитного поля равна

Модуль вектора магнитной индукции, соответственно, равен

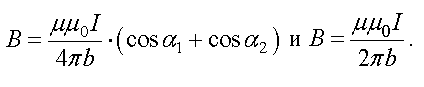
Сила Лоренца. Сила Ампера

Магнитное поле не только порождается движущимися электрическими зарядами, но действует на движущиеся заряды.

Силой Лоренца называется сила, действующая на движущийся электрический заряд со стороны магнитного поля. Сила Лоренца равна произведению заряда q на векторное произведение скорости движения заряда 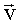и вектора магнитной индукции 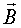, т. е.

Модуль силы Лоренца равен

где α - угол между векторам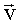и и .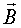

Поскольку ток - это упорядоченное движение электрических зарядов, то на проводник с током в магнитном поле тоже действует сила, которая называется силой Ампера.

Сила Ампера равна произведению силы тока на векторное произведение элемента проводника 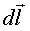и вектора магнитной индукции

Модуль силы Ампера равен

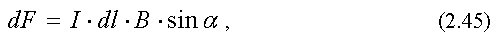
где α - угол между векторами .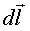

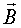С помощью измерения силы можно найти модуль вектора магнитной индукции (формула (2.45)). Сила будет максимальной, если sinα = 1. Тогда по формуле (2.45)

.

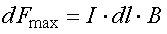Отсюда:

.

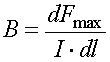Тогда единица магнитной индукции тесла (Тл) равна ньютон (Н), деленный на ампер и на метр , т. е.

.
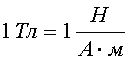