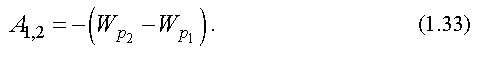Всякое тело сохраняет состояние покоя или равномерного и прямолинейного движения, пока воздействие на него других тел не заставит изменить его это состояние.

Первый закон Ньютона (также, как другие) выполняется только для инерциальных систем отсчета. Инерциальной системой отсчета называется такая система отсчета, относительно которой тело, свободное от внешних воздействий, либо покоится, либо движется равномерно и прямолинейно.

II закон Ньютона называют основным законом динамики поступательного движения. Приняты такие две формулировки. Первая формулировка справедлива для движения тел с постоянной массой.

Результирующая сила, действующая на тело, равна массе тела, умноженной на его ускорение

где .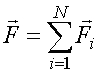

Вторая формулировка является более общей, она справедлива для движения тел как для классической, так и для релятивистской механики. Она читается так: результирующая сила, действующая на тело, равна производной по времени от импульса тела

Отсюда: 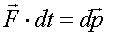или .

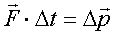Произведение силы на время ее действия называется импульсом силы. Следовательно, импульс силы равен изменению импульса тела.

III закон Ньютона носит название закона взаимодействия. Он утверждает, что всякое действие тел друг на друга носит характер взаимодействия.

При взаимодействии тел сила, действующая со стороны первого тела на второе, равна по величине и противоположна по направлению силе, действующей со стороны второго тела на первое.

Эти силы приложены к разным телам, всегда действуют парами и являются силами одной природы. Например, на рис. 1.7 показаны гравитационные силы, действующие между двумя телами.

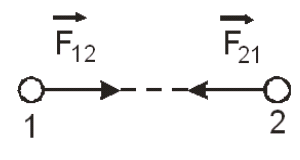
Рис.1.7

Этот закон позволяет осуществить переход от динамики отдельной материальной точки к динамике системы материальных точек. Это следует из того, что для системы материальных точек взаимодействие сводится к силам парного взаимодействия между материальными точками.

Единицей измерения силы в системе СИ является ньютон (Н)

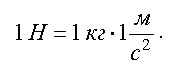
Закон сохранения импульса

Закон сохранения импульса является одним из основных законов природы. В механике его можно получить из II и III законов Ньютона. Он справедлив для системы материальных точек, на которые либо не действуют внешние силы, либо векторная сумма всех внешних сил равна нулю. Система, на которую не действуют внешние силы, называется замкнутой системой.

Для вывода закона сохранения импульса рассмотрим замкнутую систему, состоящую из трех тел. (рис. 1.8). Тогда между телами системы действуют только внутренние силы.

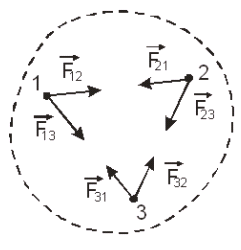
Рис.1.8

По III закону Ньютона (1.24)

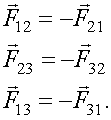
По II закону Ньютона (1.23)

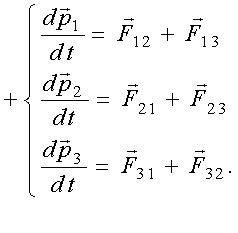
Сложим левые и правые части уравнений

.

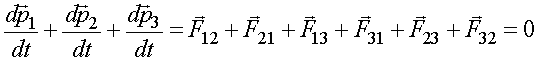Преобразуем это уравнение

.

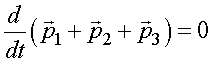Назовем 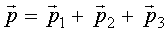импульсом системы.

Импульсом системы называется векторная сумма импульсов тел, входящих в систему.

Тогда: 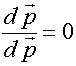и 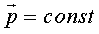, если внешние силы отсутствуют.

Закон сохранения импульса читается так: импульс замкнутой системы сохраняется.

Отметим, что импульс сохраняется и для незамкнутых систем при условии, что векторная сумма внешних сил равна нулю.

На основе закона сохранения импульса можно объяснить отдачу оружия при стрельбе, реактивное движение и т. д. Закон сохранения импульса является одним из важнейших законов природы. Он выполняется всегда и везде - в космосе и микромире, для макротел и микрочастиц.

Работа в механике. Мощность

Понятие работа является обобщением повседневного опыта человека. Но в механике это понятие является более узким и более точным, чем в быту.

Работой постоянной силы в механике называется произведение модуля вектора силы на модуль вектора перемещения и на косинус угла между направлением силы и направлением перемещения (рис. 1.9)

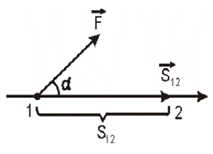
Рис.1.9

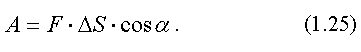
Эта формула справедлива, если тело движется прямолинейно и на него действует постоянная сила. Длина пути тогда равна модулю вектора перемещения .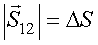

Из формулы (1.25) следует, что работа может быть положительной (если 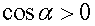), отрицательной ( 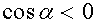) или равной нулю ( 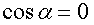). Если работа положительная ( A > 0 ), то это значит, что внешние силы совершают над телом работу. Если работа отрицательная ( A < 0 ), то тело совершает работу над внешними телами.

Единицей работы в системе СИ является джоуль (Дж)

.

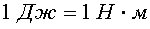В общем случае, движение может происходить по криволинейной траектории под действием переменной силы (рис. 1.10).

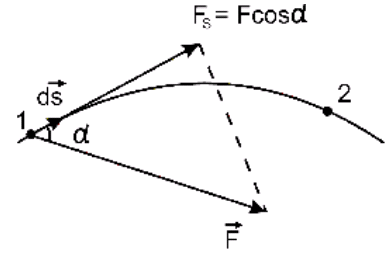
Рис.1.10

Тогда сначала нужно вычислить элементарную работу на малом участке пути, на котором движение можно считать прямолинейным, а силу постоянной

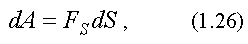
где 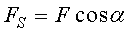; F_s - проекция силы на направление перемещения.

Суммарную работу находят интегрированием

По этой формуле вычисляется работа переменной силы.

Работа, совершаемая в единицу времени, называется мощностью

Единица мощности - ватт (Вт)

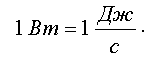
Механическая энергия

Проблема энергии касается каждого человека. От потребления энергии непосредственно зависит благосостояние людей, поэтому надо четко представлять себе, что такое энергия, и как она распределяется.

В соответствии с различными формами движения материи существуют разные виды энергии: механическая, химическая, тепловая, электрическая, ядерная и т. д. Для сравнения различных форм движения материи требуется общий эквивалент, подобно тому, как деньги являются общим эквивалентом, позволяющим сравнивать различные товары. В физике мерой перехода одних форм движения в другие является энергия. Изменение энергии связано с совершением работы. Итак, энергией называется способность тела совершать работу.

В механике тело способно совершить работу в двух случаях:

1) если оно движется, т. е. обладает кинетической энергией;

2) если оно находится в потенциальном поле сил, т. е. обладет потенциальной энергией.

Кинетическая энергия

Кинетической энергией называется энергия движущегося тела. Найдем формулу для кинетической энергии и покажем, что изменение кинетической энергии равно работе равнодействующей силы.

Элементарная работа равна

.

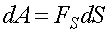Используя формулы (1.22), (1.8), (1.5), получим

.

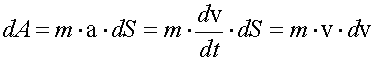Суммарная работа по формуле (1.27) равна

.

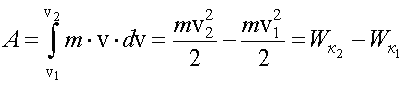Отсюда кинетическая энергия вычисляется по формуле

Кинетическая энергия всегда положительная, она измеряется в тех же единицах, что и работа. Если A > 0, то 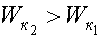, т. е. кинетическая энергия тела возрастает, следовательно, внешние силы над телом совершают работу.

Если A<0, то 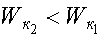, т. е. кинетическая энергия тела убывает, значит тело совершает работу.

Консервативные силы

Примерами консервативных сил являются сила тяжести и сила упругости.

Основным свойством консервативных сил является то, что работа консервативных сил не зависит от формы траектории. Покажем это на примере работы силы тяжести ( 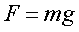, см. формулу (1.18)).

Покажем, что работа силы тяжести (формула (1.25)) одинакова для двух разных путей (для пути 1 - 3 и пути 1 - 2 - 3), обозначения длин путей приведены на рис. 1.11

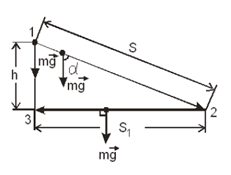
Рис.1.11

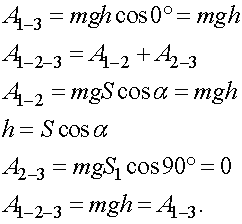
Из последней формулы следует, что работа силы тяжести не зависит от формы траектории.

Консервативными силами называются силы, работа которых не зависит от формы траектории, а определяется только начальной и конечной координатами тел. Силы, которые не удовлетворяют этому правилу, называются неконсервативными. Примером неконсервативных сил является сила трения.

Потенциальная энергия

Потенциальной энергией называется энергия, обусловленная взаимным расположением тел или их частей друг относительно друга.

Универсальной формулы для расчета потенциальной энергии нет.

Потенциальная энергия гравитационного взаимодействия двух тел равна:

где m₁ и m₂ - массы взаимодействующих тел, r - расстояние между центрами масс, 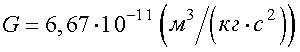- гравитационная постоянная.

Потенциальная энергия тела, поднятого на высоту h, равна

где 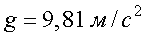- ускорение свободного падения.

Потенциальная энергия упруго сжатой пружины равна

где k - коэффициент упругости, 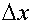- деформация (изменение длины тела).

Работа в потенциальном поле сил равна убыли потенциальной энергии: