Измерение и обработка результатов

В стеклянной газоразрядной трубке, наполненной водородом, с помощью пускового устройства (блока питания) зажигают тлеющий разряд. Электроны и ионы газоразрядной плазмы, сталкиваясь с атомами водорода, переводят их в возбужденное состояние, последние, возвращаясь в стационарное состояние, излучают световые кванты. Но поскольку водород – это газ, большинство молекул которого являются двухатомными, то на изучаемый нами линейчатый спектр атомарного водорода накладывается полосатый спектр излучения водорода молекулярного, чем и объясняется наличие множества слабых оранжево-желтых и темно-зеленых полос между линиями Н_αи Н_β .

Наблюдение спектра излучения водорода осуществляется с помощью монохроматора.

1. Включают пусковое устройство и, глядя в окуляр монохроматора, вращением барабана добиваются хорошей видимости красной линии Н_α (см.инструкцию на установке). Определяют положение красной линии, ведя отсчет в углах поворота барабана монохроматора. Аналогично определяют положение остальных линий серии Бальмера.

2. Пользуясь градуировочной кривой, находят длины волн излучения, соответствующие линиям Н_α, Н_β, Н_γ, Н_δ, и заносят их в таблицу.

3. Рассчитывают частоту излучения α, β, γ, δквантов по формуле (3.10.12).

4. По известным для каждой линии главным квантовым числам и подсчитанной частоте кванта по формуле (3.10.11) определяют опытное значение постоянной Ридберга.

5. По формуле (3.10.10) вычисляют теоретическое значение постоянной Ридберга.

6. Определяют ошибку опытного значения по отношению к теоретическому по формуле:

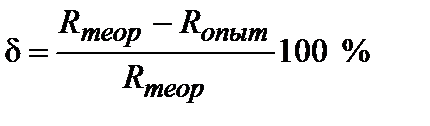(3.10.13)

Все вычисления вести в системе СИ, используя следующие значения физических постоянных:

с = 3·108 м/с; ε₀ = 8,85·10^-12Ф/м; m = 9,1·10^-31кг;

h = 6,63·10^-34 Дж·с; е = 1,6·10^-19Кл.

Опытные и расчетные данные сводят в таблицу:

Цвет и индекс спектральной линии водорода	Длина волны	Частота квантов	Квантовые числа	Постоянная Ридберга	Относит. ошибка, %
А	м	n1	n2	из опыта	по формуле
ярко-красная
зелено-голубая
фиолетовая
слабо-фиолетовая
среднее значение

Контрольные вопросы

1. Какой должен быть спектр излучения атома водорода по модели Резерфорда?

2. Как формулируются постулаты Бора?

3. Как рассчитать полную энергию электрона в атоме?

4. Что такое основное (нормальное) и возбужденное состояние электрона в атоме?

5. Что такое спектр излучения, серия излучения, линия излучения?

6. Какие бывают спектры излучения и поглощения?

7. В чем состоят недостатки боровской теории атома?

8. Докажите, что линию α в серии Лаймана невозможно наблюдать визуально.

Литература

1. Савельев И.В. Курс общей физики. Т.3.Учеб. пособие для студентов втузов. – М.: КНОРУС, 2009, 368 с.

2. Трофимова Т.И. Курс физики. Учеб. пособ. для вузов.- 15-е изд., стереотип. – М.: Издательский центр «Академия», 2007. – 560 с.

3. Детлаф А.А., Яворский Б.М. Курс физики. Учеб пособие для втузов. – М: Высш. Шк., 1989. – 608 с.

ЛАБОРАТОРНАЯ РАБОТА № 3.21

ОПРЕДЕЛЕНИЕ ФОКУСНЫХ РАССТОЯНИЙ ЛИНЗ

МЕТОДОМ БЕССЕЛЯ

Цель работы:изучение методов определения фокусных расстояний тонких линз.

Теоретические положения

Линзойназывается прозрачное тело, ограниченное двумя криволинейными или криволинейной и плоской поверхностями. Обычно применяют линзы, поверхности которых имеют сферическую форму. Основные типы линз изображены на рис. 3.21.1.

Различают тонкие и толстые линзы. Линза называется тонкой, если её толщиной можно пренебречь по сравнению с радиусами кривизны её поверхностей.

Система, состоящая из одной или нескольких линз, называется центрированной, если центры кривизны всех её преломляющих поверхностей лежат на одной прямой, называемой оптической осью.

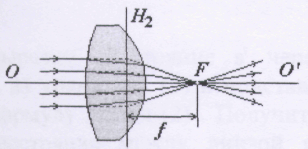
Рассмотрим основные свойства центрированной системы на примере толстой двояковыпуклой стеклянной линзы, находящейся в воздухе. Лучи, проходящие через первый главный фокус F₁, выходят с другой стороны линзы пучком, параллельным главной оптической оси ОО' (рис. 3.21.2). Главной плоскостью называется геометрическое место точек пересечения падающих лучей с их продолжениями за линзой. Главный фокус находится на расстоянии −f₁ от первой главной плоскости H₁. Здесь и далее всем расстояниям, отсчитываемым против хода лучей, приписывается знак "−" (правило знаков).

Пучок лучей, падающих на линзу параллельно главной оптической оси, сходится во втором главном фокусе F₂, отстоящем на расстоянии f₂ от второй главной плоскости H₂ (рис. 3.21.2').

Если по обе стороны от линзы находится одна и та же среда, фокусные расстояния совпадают: -f₁ = f₂ = f. Величина D = 1/f называется оптической силой линзы.

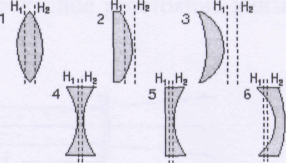
Рис. 3.21.1. Основные типы линз и положение их главных плоскостей: собирающие: 1- двояковыпуклая, 2 – плоско-выпуклая, 3 – вогнуто- выпуклая (положительный мениск); рассеивающие: 4 – двояковогнутая, 5 – плоско-вогнутая, 6 – выпукло-вогнутая (отрицательный мениск).

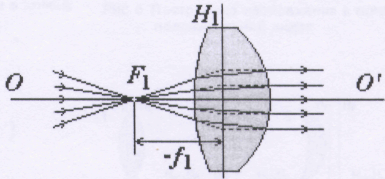
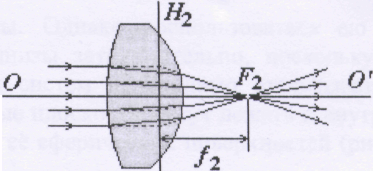
Рис. 3.21.2. Прохождение пучка лучей, сходя­щихся в первом главном фокусе F1, через двояковыпуклую линзу

Рис. 3.21.2'. Прохождение пучка лучей, парал­лельного оптической оси, через двояковыпуклую линзу

Собирающая линза сводит лучи, параллельные оптической оси, в действительном фокусе (f > 0, рис. 3.21.3), и имеет положительную оптическую силу.

Оптическая сила рассеивающей линзы отрицательна, так как для неё точка схождения параллельных лучей мнимая (f < 0, рис. 3.21.4).

Для тонкой линзы можно считать, что точки пересечения её поверхностей с оптической осью сливаются в одну точку, называемую оптическим центром, а главные плоскости H₁, Н₂ – в одну плоскость, проходящую через оптический центр линзы перпендикулярно её главной оптической оси.

Рис. 3.21.3. Собирающая линза сводит пучок лучей, параллельных ОО', в действительном фокусе.

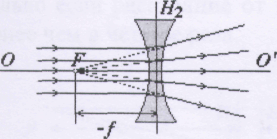
Если светящийся пред­мет – небольшой отрезок, перпендикулярный к оптической оси, то его изображение, полученное с помощью параксиальных (приосе­вых) лучей, также имеет вид отрезка, перпендикулярного к оптической оси (рис. 3.21.5). Расстояния до предмета и до его изображения s и s', отсчитанные от оптического центра вдоль главной оптической оси и взятые с учётом правила знаков, подчиняются уравнению линзы (3.21.1)

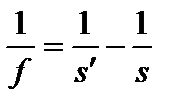, (3.21.1)

где f – фокусное расстояние линзы, s' – расстояние до изображения, s – расстояние до предмета.

Рис. 3.21.4. Такой же пучок после преломления в рассеивающей линзе кажется исходящим из мнимого фокуса.

Для тонкой собирающей линзы f можно рассчитать по этой формуле, получив действительное изображение предмета и измерив расстояния s и s'.

Формула (3.21.1) справедлива и для толстой линзы. Однако воспользоваться ею для определения фокусного расстояния произвольной линзы затруднительно, поскольку все расстояния в случае толстых линз или оптических систем необходимо отсчитывать от соответствующих главных плоскостей (рис. 3.21.6). Главные плоскости могут лежать и внутри, и вне линзы, совершенно несимметрично относительно её сферических поверхностей (рис. 3.21.1), и их положение, как правило, неизвестно.

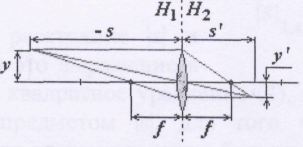
Рис. 3.21.5. Построение изображения в тонкой положительной

линзе.

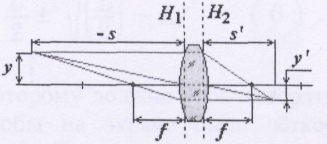
Рис. 3.21.6 Построение изображения в толстой положительной

линзе.

Содержание работы

Удобным методом определения фокусного расстояния является используемый в данной работе метод Бесселя, который позволяет найти величину f, не зная положения главных плоскостей линзы.

С одной стороны от положительной линзы на её оптической оси поместим предмет, действительное изображение которого будем получать на экране, расположенном с другой стороны от линзы. Расстояние L между предметом и экраном зафиксируем. Если оно достаточно велико, существуют два положения линзы, при которых на экране получаются чёткие изображения предмета – уменьшенное и увеличенное (рис. 3.21.7).

Найдём эти положения из уравнения

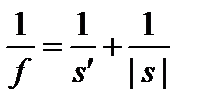(3.21.2)

и условия

|s| + s' = L. (3.21.3)

В формуле (3.21.3) мы пренебрегли расстоянием между главными плоскостями линзы по сравнению с L.

Выразим расстояние s' через расстояние |s| и L из уравнения (3.21.3) и подставим это выражение в формулу линзы (3.21.2). Получится квадратное уравнение (3.21.4), которому должно удовлетворять расстояние между линзой и предметом s, для того чтобы на экране было чёткое изображение.

|s|² – L|s| + Lf = 0. (3.21.4)

Если дискриминант этого уравнения больше нуля, то есть

L^{2 –} 4Lf ≥ 0 или L ≥ 4f, (3.21.5)

то существуют два решения (3.21.6), симметричных относительно середины промежутка предмет – экран.

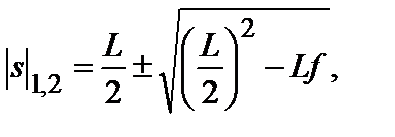
(3.21.6)

Условие (3.21.5) фактически означает, что чёткое изображение на экране можно получить, только если расстояние от предмета до экрана превосходит фокусное расстояние линзы не менее чем в четыре раза.

Расстояние А между двумя положениями линзы, которым соответствуют увеличенное и уменьшенное изображения предмета (см. рис. 3.21.7), равно разности расстояний |s|₁ и |s|₂ и выражается через L и f :

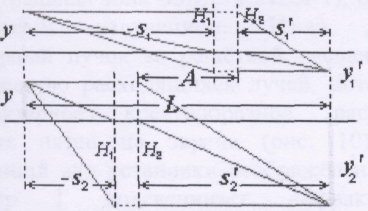
Рис. 3.21.7. Получение двух изображений по методу Бесселя.

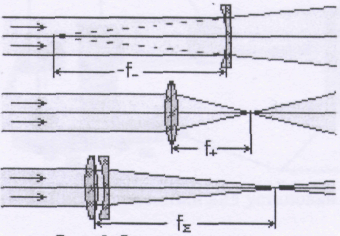
Рис. 3.21.8.Сложение линз.

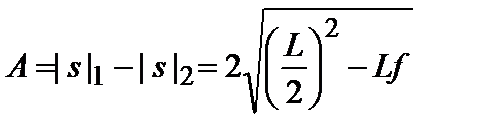. (3.21.7)

Решая уравнение (3.21.7) относительно фокусного расстояния, приходим к формуле определения фокусного расстояния по методу Бесселя:

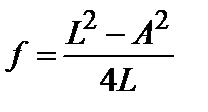. (3.21.8)

Полученная формула позволяет найти f, измерив отрезки L и А, длины которых не зависят от положения главных плоскостей линзы, что и является главным достоинством метода Бесселя.

Непосредственно с помощью метода Бесселя определить фокусное расстояние рассеивающей линзы невозможно, так как такая линза не даёт действительных изображений предмета. Однако, если рассеивающую линзу вплотную сложить с более сильной собирающей линзой, получится собирающая оптическая система (рис. 3.21.8). По методу Бесселя можно определить фокусные расстояния собирающей линзы и получившейся системы, а фокусное расстояние рассеивающей линзы рассчитать, исходя из них. Аналогично можно рассчитать фокусное расстояние второй собирающей линзы, если ее оптическая сила мала, и она не формирует сопряженных положений на данной базе L.

При сложении линз вплотную их оптические силы складываются в соответствии с уравнением (3.21.9):

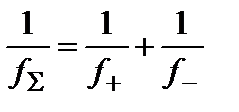. (3.21.9)

Из этого уравнения получается формула (3.21.10)

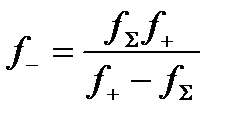, (3.21.10)

по которой можно найти фокусное расстояние второй линзы.

Искажения изображений в оптических системах называются аберрациями. Дисторсией называют одну из аберраций оптических систем, для которой характерно нарушение геометрического подобия между объектом и его изображением. Дисторсия обусловлена неодинаковостью линейного оптического увеличения на разных участках изображения (см. рис. 3.21.9, 3.21.10).

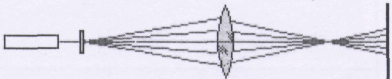
Рис. 3.21.9. Ход лучей при наблюдении дисторсии.

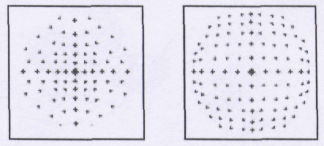
Рис. 3.21.10. Распределение пятен на экране при подушкообразной

и бочкообразной дисторсии

Описание оборудования

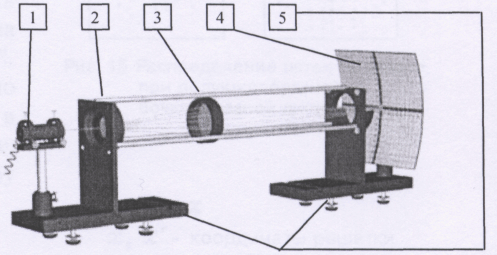
Рис. 3.21.11. Внешний вид установки.

Рис 3.21.12. Объект МОЛ- 1.

Опыты могут быть проведены на лабораторных установках РМС1 и РМС4. Установки имеют сходную конструкцию оптической скамьи стержневого типа. Линзы в оправах размещаются между стержнями и могут перемещаться вдоль них. Для отсчета расстояний вдоль оптической оси служит натянутая лента рулетки, закрепленная с помощью специальных зажимов в стойках. Для имитации светящегося предмета в работе РМС1 применяется двумерная дифракционная решётка (центральная зона объекта МОЛ-1), освещаемая лазерным излучением. Из-за дифракции лазерный пучок за решёткой расщепляется на множество расходящихся лучей, которые дают характерное крестообразное расположение ярких пятен на экране (рис. 3.21.10). Полный внешний вид установки изображён на рис. 3.21.11. Лазер 1 подсвечивает дифракционную решётку 2. Пятно, возникающее на решётке при освещении её лазерным лучом, играет роль светящегося "предмета". Расходящиеся от "предмета " лучи исследуемая линза или система линз 3 сводит на экране 4 в пятно-изображение. Элементы установки размещены на оптической скамье 5.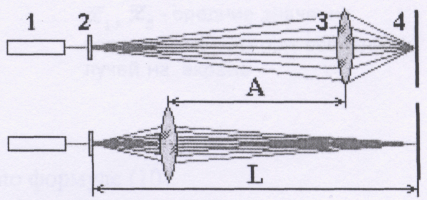

Рис. 3.21.13. Расстояния, используемые в методе Бесселя.

Порядок выполнения работы

1. Прочесть инструкцию на рабочем месте.

2. Убрать линзы из оптического тракта. Включить лазер. Проверить правильность установки лазера, решетки и экрана. При правильной установке центральное дифракционное пятно должно находиться в центре экрана и иметь круглую форму. Кроме того, при перемещении решетки вдоль оси на 20 см центральное пятно должно смещаться не более чем на 1 мм.

3. Установить решётку и экран на расстоянии, указанном преподавателем, и определить их координаты х и х' по шкале оптической скамьи.

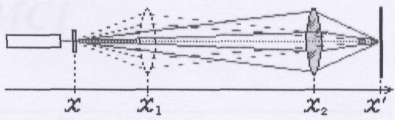
Рис. 3.21.14. Координаты решётки x, экрана x', положений линзы x₁ и x₂.

4. Установить в тракт первую линзу и, перемещая её, найти координаты x₁ и x₂ положений, при которых линза сводит лучи на экране в увеличенное и уменьшенное пятно-изображение. Повторить измерение координаты каждого положения три раза. Результаты занести в таблицу 1 (см. рис. 3.21.13).

5. Установить в тракт вторую линзу. Произвести измерения п. 4 с системой, составленной из двух линз.

6. Вынуть обе линзы из оптической скамьи и установить экран так, чтобы были отчётливо видны пятна между лучами основного яркого "креста". Для наблюдения дисторсии установить линзу приблизительно посередине между решёткой и экраном (см. рис. 3.21.9). Помещая в тракт сначала одну линзу, затем обе линзы вместе, зарисовать в каждом случае структуру распределения световых пятен на экране.

Обработка результатов

1. Вычислить расстояние L:

L = x' – х,

x, x' – координаты решётки и экрана.

2. Найти средние значения координат x₁ и x₂ для первой линзы и системы линз и определить по ним расстояние А в обоих случаях.

А = ,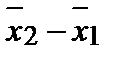

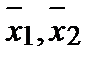– средние значения координат линзы при сведении лучей на экране.

3. Определить фокусные расстояния первой линзы и системы линз по формуле (8).

4. Рассчитать фокусное расстояние второй линзы по формуле (10).

5. На основе сделанных зарисовок определить характер дисторсии для системы из двух линз и для каждой линзы в отдельности.

Таблица 1

№ опыта				xср.	A	L	f
x1
x2

Контрольные вопросы

1. Что называется линзой? Что такое тонкие и толстые линзы? Каковы основные типы линз?

2. Что такое центрированная оптическая система, оптическая ось, главный фокус и главная плоскость линзы?

3. Что такое оптическая сила и оптический центр линзы?

4. Как записывается уравнение тонкой линзы?

5. Как строятся изображения в собирающих и рассеивающих линзах?

6. Каковы положения главных плоскостей для различных линз?

7. В чем заключается метод Бесселя?

8. Как определяется фокусное расстояние рассеивающей линзы по методу Бесселя?

9. Что называют дисторсией оптической системы? Каковы виды дисторсии?

Литература

1. Детлаф А.А., Яворский Б.М. Курс физики. Учеб пособие для втузов. – М: Высш. Шк., 1989. – 608 с.

2. Савельев И.В. Курс общей физики. Т.2.Учеб. пособие для студентов втузов. – М.: КНОРУС, 2009, 576 с.

3. Трофимова Т.И. Курс физики. Учеб. пособие для вузов.- 15-е изд., стереотип. – М.: Издательский центр «Академия», 2007. –560 с.

ЛАБОРАТОРНАЯ РАБОТА № 3.22