Принцип наименьшего действия

В XVIII веке происходит дальнейшее накопление и систематизация научных результатов, отмеченные тенден­цией объединения отдельных научных достижений в стро­го упорядоченную, связную картину мира с помощью систематического применения методов математическо­го анализа к исследованию физических явлений. Рабо­та многих блестящих умов в этом направлении привела к созданию базисной теории механистической исследова­тельской программы — аналитической механики, на осно­ве положений которой были созданы различные фунда­ментальные теории, описывающие конкретный класс конк-

ретных явлений: гидродинамика, теория упругости, аэро­динамика и т. д. Одним из важнейших результатов ана­литической механики является принцип наименьшего действия (вариационный принцип), имеющий важное зна­чение для понимания процессов, происходящих в физике конца XX века.

Корни возникновения вариационных принципов в на­уке уходят в Древнюю Грецию и связаны с именем Геро-на из Александрии. Идея любого вариационного принци­па состоит в том, чтобы варьировать (изменять) некоторую величину, характеризующую данный процесс, и отбирать из всех возможных процессов тот, для которого данная вели­чина принимает экстремальное (максимальное или мини­мальное) значение. Герон попытался объяснить законы отражения света, варьируя величину, характеризующую длину пути, проходимым лучом света от источника к на­блюдателю при отражении его от зеркала. Он пришел к выводу, что из всех возможных путей луч света выбирает кратчайший (из всех геометрически возможных).

В XVII веке, спустя две тысячи лет, французский мате­матик Ферма обратил внимание на принцип Герона, распро­странил его для сред с различными показателями прелом­ления, переформулировав его в связи с этим в терминах времени. Принцип Ферма гласит: в преломляющей среде, свойства которой не зависят от времени, световой луч, про­ходя через две точки, выбирает себе такой путь, чтобы вре­мя, необходимое ему для прохождения от первой точки ко второй, было минимальным. Принцип Герона оказывается частным случаем принципа Ферма для сред с постоянным коэффициентом преломления.

Принцип Ферма привлек пристальное внимание со­временников. С одной стороны, он как нельзя лучше сви­детельствовал о «принципе экономии» в природе, о ра­циональном божественном замысле, реализованном в уст­ройстве мира, с другой — он противоречил ньютоновской корпускулярной теории света. Согласно Ньютону получа­лось, что в более плотных средах скорость света должна быть больше, в то время как из принципа Ферма вытека­ло, что в таких средах скорость света становится меньшей.

В 1740 году математик Пьер Луи Моро де Мопертюи, критически анализируя принцип Ферма и следуя теоло-

гическим мотивам о совершенстве и наиболее экономном устройстве Вселенной, провозгласил в работе «О различ­ных законах природы, казавшихся несовместимыми» принцип наименьшего действия. Мопертюи отказался от наименьшего времени Ферма и ввел новое понятие — дей­ствие. Действие равняется произведению импульса тела (количества движения Р = mV) на пройденный телом путь. Время не имеет какого-либо преимущества перед простран­ством, равно как и наоборот. Поэтому свет выбирает не кратчайший путь и не наименьшее время для его прохож­дения, а согласно Мопертюи, «выбирает путь, дающий бо­лее реальную экономию: путь, по которому он следует, — это путь, на котором величина действия минимальна». Принцип наименьшего действия в дальнейшем был развит в работах Эйлера и Лагранжа; он явился основой, на ко­торой Лагранж развил новую область математического анализа — вариационное исчисление. Дальнейшее обобще­ние и завершенную форму этот принцип получил в рабо­тах Гамильтона. В обобщенном виде принцип наименьше­го действия использует понятие действия, выраженного не через импульс, а через функцию Лагранжа. Для случая од­ной частицы, движущейся в некотором потенциальном поле, функция Лагранжа может быть представлена как разность кинетической 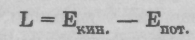и потенциальной энергии:

(Понятие «энергия» подробно обсуждается в главе 3 настоящего раздела.)

Произведение 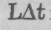называется элементарным действи­ем. Полным действием называется сумма всех значений 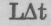на всем рассматриваемом интервале времен, иными словами, полное действие А:

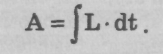
Уравнения движения частицы могут быть получены с помощью принципа наименьшего действия, согласно которо­му реальное движение происходит так, что действие оказы­вается экстремальным, то есть его вариация обращается в 0:

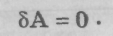
Вариационный принцип Лагранжа-Гамильтона легко допускает распространение на системы, состоящие из не-

скольких (множества) частиц. Движение таких систем обыч­но рассматривают в абстрактном пространстве (удобный ма­тематический прием) большого числа измерений. Скажем, для N точек вводят некоторое абстрактное пространство 3N координат N частиц, образующих систему, называемую конфи­гурационным пространством. Последовательность различных состояний системы изображается кривой в этом конфигу­рационном пространстве — траекторией. Рассматривая все возможные пути, соединяющие две заданные точки это­го 3N-Mepнoгo пространства, можно убедиться, что реаль­ное движение системы происходит в соответствии с прин­ципом наименьшего действия: среди всех возможных тра­екторий реализуется та, для которой действие экстремально по всему интервалу времени движения.

При минимизации действия в классической механике получают уравнения Эйлера-Лагранжа, связь которых с законами Ньютона хорошо известна. Уравнения Эйлера-Лагранжа для лагранжиана классического электромагнит­ного поля оказываются уравнениями Максвелла. Таким образом, мы видим, что использование лагранжиана и прин­ципа наименьшего действия позволяет задавать динамику частиц. Однако лагранжиан обладает еще одной важной особенностью, что и сделало лагранжев формализм основ­ным в решении практически всех задач современной фи­зики. Дело в том, что наряду с ньютоновской механикой в физике уже в XIX веке были сформулированы законы со­хранения для некоторых физических величин: закон со­хранения энергии, закон сохранения импульса, закон сохра­нения момента импульса, закон сохранения электрическо­го заряда. Число законов сохранения в связи с развитием квантовой физики и физики элементарных частиц в на­шем столетии стало еще больше. Возникает вопрос, как найти общую основу для записи как уравнений движения (скажем, законов Ньютона или уравнений Максвелла), так и сохраняющихся во времени величин. Оказалось, что та­кой основой является использование лагранжева форма­лизма, ибо лагранжиан конкретной теории оказывается инвариантным (неизменным) относительно преобразований, соответствующих конкретному рассматриваемому в данной теории абстрактному пространству, следствием чего и яв­ляются законы сохранения. Эти особенности лагранжиа-

на привели к целесообразности формулировки физических теорий на языке лагранжианов. Осознание этого обстоя­тельства пришло в физику благодаря возникновению тео­рии относительности Эйнштейна.