Вращательное движение твердых тел
Основные формулы
· Момент инерции материальной точки:
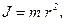
где 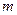 — масса точки;
— масса точки; 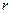 — расстояние до оси вращения.
— расстояние до оси вращения.
· Момент инерции механической системы (тела) относительно неподвижной оси:
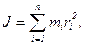
где 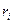 - расстояние материальной точки массой
- расстояние материальной точки массой 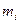 до оси вращения; в случае непрерывного распределения масс:
до оси вращения; в случае непрерывного распределения масс:
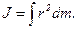
· Моменты инерции тел правильной геометрической формы (тела считаются однородными; 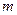 — масса тела):
— масса тела):
| Тело | Положение оси вращения | Момент инерции |
Обруч или полый тонкостенный цилиндр радиусом 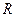 | Ось симметрии проходит через центр цилиндра | 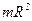 |
Сплошной цилиндр или диск радиусом 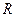 | Ось симметрии проходит через центр цилиндра (диска) | 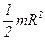 |
Прямой тонкий стержень длиной 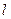 | Ось перпендикулярна стержню и проходит через его середину | 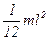 |
Прямой тонкий стержень длиной 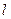 | Ось перпендикулярна стержню и проходит через его конец | 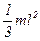 |
Шар радиусом 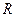 | Ось проходит через центр шара | 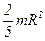 |
· Теорема Штейнера:
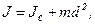
где 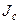 – момент инерции тела относительно оси, проходящей через центр масс;
– момент инерции тела относительно оси, проходящей через центр масс; 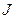 – момент инерции относительно параллельной оси, отстоящей от первой на расстоянии
– момент инерции относительно параллельной оси, отстоящей от первой на расстоянии 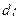
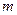 - масса тела.
- масса тела.
· Момент силы относительно неподвижной точки:
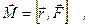
где 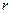 – радиус-вектор, проведенный из этой точки в точку приложения силы
– радиус-вектор, проведенный из этой точки в точку приложения силы 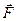 . Модуль момента силы относительно неподвижной оси:
. Модуль момента силы относительно неподвижной оси:
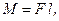
где 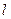 - плечо силы (кратчайшее расстояние между линией действия силы и осью вращения).
- плечо силы (кратчайшее расстояние между линией действия силы и осью вращения).
· Основной закон динамики вращательного движения твердого тела:
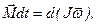
где 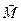 - момент сил, приложенных к телу;
- момент сил, приложенных к телу; 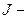 момент инерции тела относительно оси вращения;
момент инерции тела относительно оси вращения; 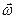 - угловая скорость тела.
- угловая скорость тела.
· Уравнение (закон) динамики вращательного движения твердого тела относительно неподвижной оси:
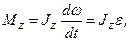
где 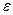 - угловое ускорение;
- угловое ускорение; 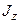 - момент инерции тела относительно оси z.
- момент инерции тела относительно оси z.
· Момент импульса (момент количества движения) твердого тела относительно оси вращения:
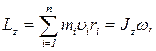
где 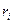 - расстояние от оси
- расстояние от оси 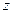 до отдельной частицы тела;
до отдельной частицы тела; 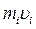 - импульс этой частицы;
- импульс этой частицы; 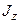 - момент инерции тела относительно оси
- момент инерции тела относительно оси 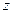 ;
; 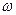 - его угловая скорость.
- его угловая скорость.
· Закон сохранения момента импульса для замкнутой системы:
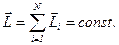
· Работа при вращательном движении тела:
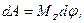
где 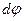 - угол поворота тела;
- угол поворота тела; 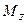 - момент силы относительно оси
- момент силы относительно оси 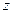 .
.
· Кинетическая энергия тела, вращающегося вокруг неподвижной оси 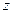 :
:
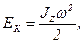
где 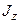 – момент инерции тела относительно оси
– момент инерции тела относительно оси 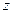 ;
; 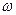 - его угловая скорость.
- его угловая скорость.
· Кинетическая энергия тела, катящегося по плоскости без скольжения:
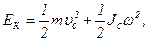
где 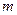 – масса тела;
– масса тела; 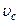 - скорость центра масс тела;
- скорость центра масс тела; 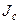 – момент инерции тела относительно оси, проходящей через его центр масс;
– момент инерции тела относительно оси, проходящей через его центр масс; 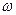 – угловая скорость тела.
– угловая скорость тела.
· Связь работы и кинетической энергии тела при вращательном движении:
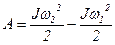 ,
,
где 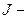 момент инерции тела относительно оси вращения;
момент инерции тела относительно оси вращения; 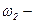 угловая скорость тела в конечном состоянии;
угловая скорость тела в конечном состоянии; 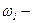 угловая скорость тела в начальном состоянии.
угловая скорость тела в начальном состоянии.
Примеры решения задач
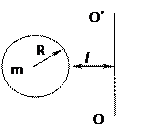
Задача 1. Найдите момент инерции шара радиусом 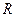 относительно оси
относительно оси 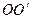 , находящейся на расстоянии
, находящейся на расстоянии 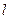 от поверхности шара (рис.3.1).
от поверхности шара (рис.3.1).
Дано: 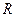 , ,  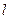 | Решение: Записываем теорему Штейнера: |
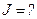 | 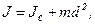 где где 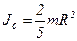 , , |
 - момент инерции шара относительно оси, проходящей через центр масс;
- момент инерции шара относительно оси, проходящей через центр масс; 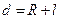 - расстояние между осями. Получаем:
- расстояние между осями. Получаем: 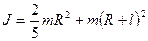 .
.
|
Задача 2.На шнуре, перекинутом через блок в виде однородного цилиндра массой 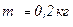 подвешены грузы массами
подвешены грузы массами 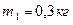 и
и 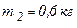 . Считаем нить невесомой и пренебрегаем трением в блоке. С каким ускорением движутся грузы? Каковы силы натяжения шнура, действующие на грузы во время движения?
. Считаем нить невесомой и пренебрегаем трением в блоке. С каким ускорением движутся грузы? Каковы силы натяжения шнура, действующие на грузы во время движения?
Дано: Решение:
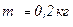 ; ; 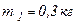 ; ; 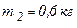 . . | Делаем рисунок, расставляем силы, дейстующие на каждое тело и на блок (рис. 3.2): 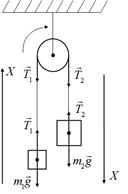 Рис.3.2 Рис.3.2 |
 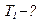 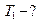 | |
Записываем второй закон Ньютона для каждого тела в векторной и скалярной форме:
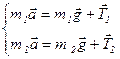
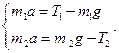 (1)
(1)
Для блока записываем основное уравнение динамики вращательного движения в векторной и скалярной форме:
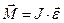
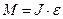 , (2)
, (2)
где 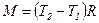 - момент сил,
- момент сил, 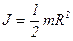 - момент инерции блока;
- момент инерции блока; 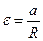 - угловое ускорение блока. Подставляя эти выражения в (2), получаем:
- угловое ускорение блока. Подставляя эти выражения в (2), получаем:
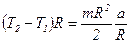 , т.е.
, т.е. 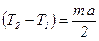 . (3)
. (3)
Решая совместно уравнения (1) и (3), получаем:
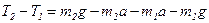 . Отсюда:
. Отсюда:
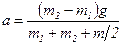 ,
,
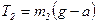 ,
, 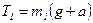 .
.
Подставляем числа: 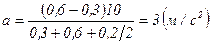 ,
,
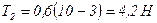 ,
,
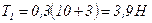 .
.
Ответ: 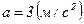 ,
, 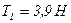 ,
, 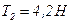 .
.
Задача 3. Шар и обруч одинаковой массы и радиуса, изготовленные из одного и того же материала, катятся без скольжения с одинаковой скоростью. Во сколько раз кинетическая энергия шара меньше кинетической энергии обруча?
Дано: Решение:
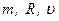 | Кинетическая энергия тела, катящегося по поверхности, складывается из кинетической энергии вращательного движения и поступательного движения центра масс: |
 |
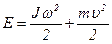 . (1)
. (1)
Моменты инерции относительно центра масс обруча 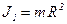 (2) и шара
(2) и шара 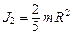 (3). Связь линейной и угловой скорости -
(3). Связь линейной и угловой скорости - 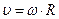 (4). Подставляя (2), (3) и (4) в (1), получаем:
(4). Подставляя (2), (3) и (4) в (1), получаем:
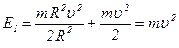 - для обруча,
- для обруча,
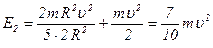 - для шара.
- для шара.
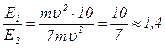
Ответ: в 1,4 раза.
Контрольные задания
3.1. Определите момент инерции сплошного однородного диска радиусом 40 см и массой 1 кг относительно оси, проходящей через середину одного из радиусов перпендикулярной плоскости диска.
3.2. Два шара одинакового радиуса R = 5 см закреплены на концах невесомого стержня. Расстояние между центрами шаров г = 0,5 м. Масса каждого шара m= 1 кг. Найдите момент инерции системы относительно оси, проходящей через середину стержня перпендикулярно к нему.
3.3. Определите момент инерции тонкого однородного стержня длиной 50 см и массой 360 г относительно оси, перпендикулярной стержню и проходящей через его конец.
3.4. Определите момент инерции тонкого однородного стержня длиной 50 см и массой 360 г относительно оси, перпендикулярной стержню и проходящей через точку, отстоящую от конца стержня на 1/6 его длины.
3.5. Длина тонкого прямого стержня 60 см, масса 100 г. Определите момент инерции стержня относительно оси, перпендикулярной к его длине и проходящей через точку стержня, удаленную на 20 см от одного из его концов.
3.6. Тонкий обруч диаметром 56 см и массой 300 г висит на гвозде, вбитом в стену. Определите его момент инерции относительно этого гвоздя.
3.7. Однородный шарик массой 100 г подвешен на нити, длина которой равна радиусу шарика. Определите момент инерции шарика относительно точки подвеса, если длина нити 20 см.
3.8. Определите момент инерции сплошного однородного цилиндра радиусом 20 см и массой 1 кг относительно оси, проходящей через образующую цилиндра.
3.9. Два шара одинакового радиуса R = 6 см закреплены на концах невесомого стержня. Расстояние между шарами г = 0,8 м. Масса каждого шара m= 2 кг. Найдите момент инерции системы относительно оси, проходящей через середину стержня перпендикулярно к нему.
3.10. Длина тонкого прямого стержня 60 см, масса 200 г. Определите момент инерции стержня относительно оси, перпендикулярной к его длине и проходящей через точку, лежащую на продолжении стержня, удаленную на 10 см от одного из его концов.
3.11. Через неподвижный блок в виде полого тонкостенного цилиндра массой 160 г перекинута невесомая нить, к концам которой подвешены грузы массами 200 г и 300 г. Пренебрегая трением в оси блока, определите ускорение грузов и силы натяжения.
3.12. На однородный сплошной цилиндрический вал радиусом 50 см намотана легкая нить, к концу которой прикреплен груз массой 6,4 кг. Груз, разматывая нить, опускается с ускорением 2 м/с2. Определите момент инерции и массу вала.
3.13. На барабан массой 9 кг намотан шнур, к концу которого привязан груз массой 2 кг. Найдите ускорение груза. Барабан считать однородным диском. Трением пренебречь.
3.14. На барабан радиусом 0,5 м намотан шнур, к концу которого привязан груз массой 1 кг. Найдите момент инерции барабана, если известно, что груз опускается с ускорением 2,04 м/с2.
3.15. Через подвижный блок в виде однородного сплошного цилиндра массой 0,2 кг перекинута невесомая нить, к концам которой прикреплены тела массами 0,35 кг и 0,55 кг. Пренебрегая трением в оси блока, определите ускорение грузов и отношение сил натяжения нити.
3.16. Тело массой 0,25 кг, соединенное невесомой нитью посредством блока (в виде полого тонкостенного цилиндра) с телом массой 0,2 кг, скользит по поверхности горизонтального стола (рис. 2.3). Масса блока 0,15 кг. Коэффициент трения тела о поверхность равен 0,2. Пренебрегая трением в подшипниках, определите ускорение, с которым будут двигаться эти тела и силы натяжения нити по обе стороны блока.
3.17. К ободу однородного сплошного диска массой 10 кг, насаженного на ось, приложена постоянная касательная сила 30 Н. Определите кинетическую энергию диска через время 4 с после начала действия силы.
3.18. Шар и сплошной цилиндр одинаковой массы, изготовленные из одного и того же материала, катятся без скольжения с одинаковой скоростью. Определите, во сколько раз кинетическая энергия шара меньше кинетической энергии сплошного цилиндра.
3.19. Обруч и диск имеют одинаковую массу и катятся без скольжения с одинаковой линейной скоростью. Кинетическая энергия обруча равна 4 Дж. Найдите кинетическую энергию диска.
3.20. Определите, во сколько раз полная кинетическая энергия обруча, скользящего вдоль наклонной плоскости, меньше полной кинетической энергии обруча, катящегося по наклонной плоскости.
3.21. На скамье Жуковского (вращающаяся без трения платформа) стоит человек и держит в руках стержень по оси скамьи. Скамья с человеком вращается с угловой скоростью 4 рад/с. С какой скоростью будет вращаться скамья с человеком, если стержень повернуть так, чтобы он занял горизонтальное положение? Суммарный момент инерции человека и скамьи 5 кг·м2, длина стержня 2 м, масса 6 кг. Считать, что центр масс стержня с человеком в обоих случаях находится на оси платформы.
3.22. На неподвижной скамье Жуковского стоит человек и держит в руке за ось велосипедное колесо, вращающееся вокруг своей оси с угловой скоростью 25 рад/с. Ось колеса расположена вертикально и совпадает с осью скамьи. С какой скоростью станет вращаться скамья, если повернуть колесо вокруг горизонтальной оси на угол 90°? Момент инерции человека и скамьи равен 2,5 кг·м2, момент инерции колеса 0,5 кг·м2.
3.23. Платформа в виде диска вращается по инерции без трения около вертикальной оси с частотой 14 мин-1. На краю платформы стоит человек. Когда человек перешел в центр платформы, частота возросла до 25 мин-1. Масса человека 70 кг. Определите массу платформы. Момент инерции человека рассчитывать, как для материальной точки.
3.24. Горизонтальная платформа массой 150 кг вращается вокруг вертикальной оси, проходящей через центр платформы с частотой 8 мин-1. Человек массой 70 кг стоит при этом на краю платформы. С какой угловой скоростью начнет вращаться платформа, если человек перейдет от края платформы к ее центру? Считать платформу круглым однородным диском, а человека - материальной точкой.
3.25. Горизонтальная платформа массой 25 кг и радиусом 0,8м вращается с частотой 18 мин-1. В центре стоит человек и держит в расставленных руках гири. Считая платформу диском, определите частоту вращения платформы, если человек, опустив руки, уменьшит свой момент инерции от 3,5 кг·м2 до 1 кг·м2.
3.26. Человек, стоящий на скамье Жуковского, держит в руках стержень длиной 2,5 м, расположенный вертикально вдоль оси вращения скамейки. Эта система (скамья и человек) обладает моментом инерции
10 кг·м2 и вращается с частотой 12 мин-1. Если стержень повернуть в горизонтальное положение так, что центр стержня совпадет с осью вращения, то частота вращения системы станет 8,5 мин-1. Определите массу стержня.
3.27. Человек массой 60 кг, стоящий на краю горизонтальной платформы радиусом 1 м и массой 120 кг, вращающейся по инерции вокруг неподвижной вертикальной оси с частотой 10 мин-1, переходит к ее центру. Считая платформу круглым однородным диском, а человека – точечной массой, определите работу, совершаемую человеком при переходе от края платформы к ее центру.
3.28. На краю неподвижной скамьи Жуковского диаметром 0,8 м и массой 6 кг стоит человек массой 60 кг. С какой угловой скоростью начнет вращаться скамья, если человек поймает летящий на него мяч массой 0,5 кг? Траектория мяча горизонтальна и проходит на расстоянии 0.4 м от оси скамьи. Скорость мяча 5 м/с.
3.29. Платформа в виде диска диаметром 3 м и массой 180 кг может вращаться вокруг вертикальной оси. С какой угловой скоростью будет вращаться эта платформа, если по ее краю пойдет человек массой 70 кг со скоростью 1,8 м/с относительно платформы?
3.30. В центре вращающегося столика стоит человек, держащий на вытянутых руках на расстоянии 150 см друг от друга две гири. Столик вращается с частотой 1 с-1. Человек сближает гири до расстояния 80 см, и частота увеличивается до 1,5 с-1. Определите работу, произведенную человеком, если каждая гиря имеет массу 2 кг. Момент инерции человека относительно оси столика считать постоянным.
