Физическая интерпретация нулевых компонент метрического тензора

Для выяснения физического смысла нулевых компонент метрических тензоров (21.6) и (21.8)

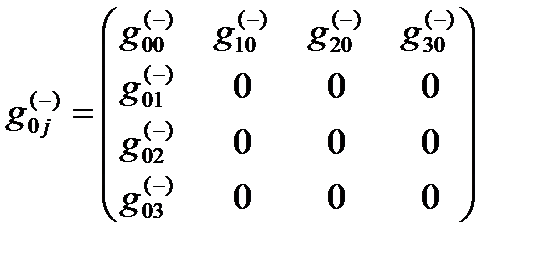, (24.1)

воспользуемся кинематикой двухсторонней 2³-l_m¸n -вакуумной протяженности.

Пусть исходное (неподвижное и неискривленное) состояние 2³-l_m¸n-вакуумной протяженности задается совокупностью псевдоевклидовых метрик (7.3) и (7.4)

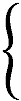ds₀^(–)2= с²dt² – dх² – dy ² – dz ² = ds^(–)¢ds^(–)¢¢ = сdt¢сdt¢¢– dx¢dx¢¢– dy¢dy¢¢– dz ¢dz¢¢, (24.2)

ds₀⁽⁺⁾²= – с²dt² +dx²+ dy ²+ dz² = ds⁽⁺⁾¢ds⁽⁺⁾¢¢ =– сdt¢сdt¢¢+ dx¢dx¢¢+ dy¢dy¢¢+dz ¢dz¢¢, (24.3)

где

ds^(–)¢ = с dt¢ + idx¢+ jdy¢+ kdz ¢ – личина субконта; (24.4)

ds^(–)¢¢ = с dt¢¢+ idx¢¢+ jdy¢¢+ kdz ¢¢ – изнанка субконта; (24.5)

ds⁽⁺⁾¢ = – с dt¢+ idx¢+ jdy¢+ kdz ¢ – личина антисубконта; (24.6)

ds⁽⁺⁾¢¢ = с dt¢¢– idx¢¢– jdy¢¢– kdz ¢¢ – изнанка антисубконта (24.7)

– аффинные агрегаты, в частности, кватернионы с таблицей умножения мнимых единиц

Таблица 24.1

	i	j	k
i	–1	k	–j
j	–k	–1	i
k	j	–i	–1

Определение № 24.1 Личина субконта – это аффинная 4-мерная протяженность с интервалом типа ds^(–)¢ = с dt¢ + idx¢+ jdy¢+ kdz ¢.

Определение № 24.2 Изнанка субконта – это аффинная 4-мерная протяженность с интервалом типа ds^(–)¢¢ = с dt¢¢+ idx¢¢+ jdy¢¢+ kdz ¢¢.

Определение № 24.3 Личина антисубконта – это аффинная 4-мерная протяженность с интервалом типа ds⁽⁺⁾¢ = – с dt¢+ idx¢+ jdy¢+ kdz ¢.

Определение № 24.4 Изнанка антисубконта – это аффинная 4-мерная протяженность с интервалом типа ds⁽⁺⁾¢¢ = с dt¢¢– idx¢¢– jdy¢¢– kdz ¢¢.

Рассмотрим четыре случая:

1). Пусть в первом случае личина и изнанка внешней и внутренней сторон 2³-l_m¸n-вакуумной протяженности (т.е. субконта и антисубконта) двигаются относительно исходного неподвижного состояния вдоль оси x с одной и той же скоростью v_x, но в разных направлениях. Это формально описывается преобразованием координат:

t¢ = t, x¢ = x + v_x t, y¢= y, z¢= z – для личины; (24.8)

t¢¢= t, x¢¢ = x – v_xt, y¢¢= y, z¢¢= z – для изнанки. (24.9)

Равенство модулей скоростей движения v_x личины и изнанки обусловлены «вакуумным условием», которое требует, чтобы каждому движению в «вакууме» соответствовало адекватное антидвижение.

Продифференцировав (24.8) и (24.9), и подставив результаты дифференцирования в метрики (24.2) и (24.3), получим совокупность метрик

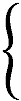ds^(–)2= (1+ v_x²/с²)c²dt²– dx² – dy² – dz²; (24.10)

ds⁽⁺⁾²= – (1+ v_x²/с²)c²dt²+ dx²+ dy²+dz² , (24.11)

описывающих кинематику совместного движения внешней и внутренней сторон 2³-l_m¸n - вакуумной протяженности (субконта и антисубконта), при соблюдении «вакуумного баланса»:

ds^(–)2 + ds⁽⁺⁾² = 0.

2). Во втором случае, пусть личина и изнанка субконта и антисубконта двигаются относительно их исходного неподвижного состояния в одном и том же направлении – вдоль оси х с одной и той же скоростью v_x. Это формально описывается преобразованиями координат:

t¢= t, x¢ = x – v_x t, y¢= y, z¢= z – для «личины»; (24.12)

t¢¢= t, x¢¢ = x – v_xt, y¢¢= y, z¢¢= z – для «изнанки». (24.13)

Продифференцировав (24.12) и (24.12) и подставив результаты дифференцирования в метрики (24.2) и (24.3), получим совокупность метрик:

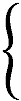ds^(–)2 = (1– v_x²/с²)c²dt² + v_xdxdt + v_xdtdx – dx² – dy²– dz², (24.14)

ds⁽⁺⁾² = – (1– v_x²/с²)c²dt² – v_xdxdt – v_xdxdt + dx²+ dy²+ dz². (24.15)

В этом случае вакуумный баланс также соблюдается, т.к. ds^(–)2 + ds⁽⁺⁾² = 0, но возникают дополнительные перекрестные слагаемые v_xdxdt.

Нулевые компоненты метрических тензоров (24.1) во втором более общем случае равны

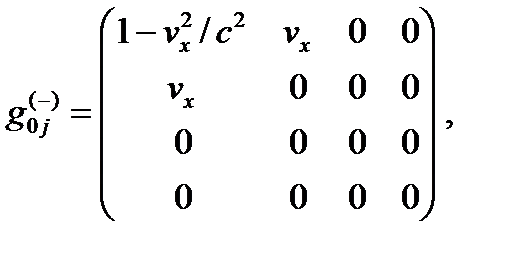
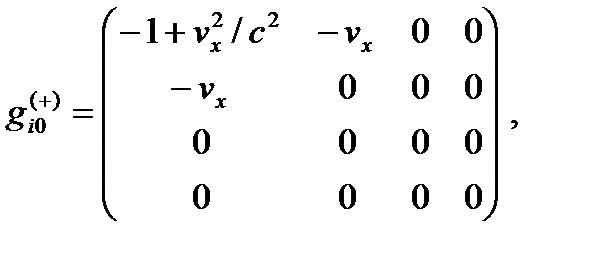(24.16)

3) Пусть личина и изнанка субконта и антисубконта (внешней и внутренней сторон 2³-l_m¸n - вакуумной протяженности) вращаются вокруг оси z в одном и том же направлении с угловой скорость W. Это описывается посредством замены переменных:

t¢ = t, x¢ = x cosW t – y sinW t, z¢ = z, y¢= x sinW t + y cosW t, (24.17)

t¢¢ = t, x¢¢ = x cosW t – y sinW t, z¢¢ = z, y¢¢ = x sinW t + y cosW t. (24.18)

Продифференцировав (24.17) и (24.18) и подставив результаты дифференцирования в метрики (24.2) и (24.3), получим интервалы [14]

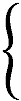ds^(–)2= [1– (W ² /с²)(х²+у²)]с²dt²+2W уdxdt – 2W хdydt – dx² – dy² – dz², (24.19)

ds^(–)2= – [1– (W ² /с²)(х²+у²)]с²dt²–2W уdxdt +2W хdydt + dx² + dy² + dz², (24.20)

В цилиндрических координатах

r ²= х²+ у², z = z , t = t , j = arctng(y/x) – W t. (24.21)

метрики (24.19) и (24.20) приобретают вид

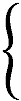ds^(–)2= (1 – r ²W ²/с²) с²dt²– r ²W /с djdt – r ²W /с dtdj – dr ² – r ²dj ²– dz², (24.22)

ds⁽⁺⁾² = – (1 – r ²W ²/с²) с²dt²+r ²W /сdjdt +r ²W /сdtdj + dr ² +r ²dj ²+ dz². (24.23)

При этом компоненты метрических тензоров (24.1) равны

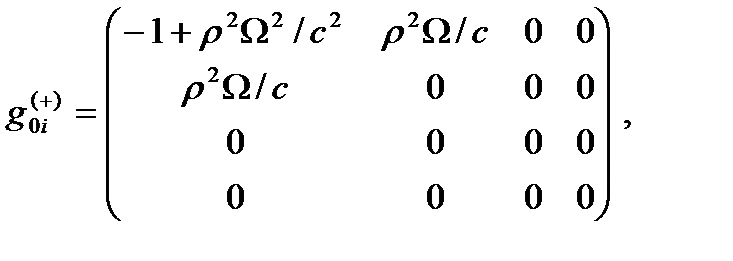(24.24)

4) Также может быть рассмотрен случай, когда личина и изнанка субконта и антисубконта вращаются во взаимно противоположных направлениях с угловой скорость W. Это описывается посредством замены переменных:

t¢ = t, x¢ = x cosW t – y sinW t, z¢ = z, y¢ = x sinW t + y cosW t,(24.25)

t¢¢= t, x¢¢ = – x cosW t + y sinW t, z¢¢= z, y¢¢ = – x sinW t – y cosW t. (24.26)

и приводит к аналогичным результатам.

Из рассмотренных примеров видно, что нулевые компоненты метрического тензора связаны с поступательным и/или вращательным движением различных сторон 2³-l_m¸n -вакуумной протяженности.

Состояние движения локального 3-мерного участка «вакуума» характеризуется усредняемыми нулевыми компонентами метрического тензора

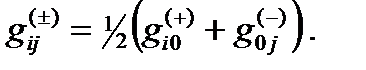(24.27)

Во всех четырех рассмотренных случаях усредненные нулевые компоненты метрического тензора (24.27) равны нулю 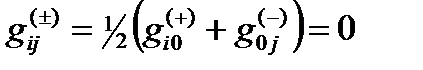. Это означает, что внутри локального 3-мерного участка «вакуума» могут протекать взаимно противоположные внутри-вакуумные процессы, но в целом этот участок остается неподвижным.

Тем не менее, возможны случаи, когда внутри-вакуумные процессы за счет фазовых сдвигов могут компенсировать друг друга не локально, а глобально. В этом случае локальный 3-мерный участок «вакуума» может участвовать (как целое) в некотором замысловатом замкнутом движении. Рассмотрим такой случай на конкретном примере. Пусть в некотором локальном участке «вакуума» кинематика внутри-вакуумных процессов такова, что

t¢ = t, x¢ = x + v_1x t, y¢= y, z¢= z – для личины субконта; (24.28)

t¢¢= t, x¢¢ = x – v_2x t, y¢¢= y, z¢¢= z – для изнанки субконта. (24.29)

t¢ = t, x¢ = x + v_3x t, y¢= y, z¢= z – для личины антисубконта; (24.30)

t¢¢= t, x¢¢ = x – v_4x t, y¢¢= y, z¢¢= z – для изнанки антисубконта, (24.31)

где v_1x ≠ v_2x ≠ v_3x ≠ v_4x , но соблюдается общий баланс движения

v_1x– v_2x + v_3x – v_4x = 0. (24.32)

В этом случае внешняя и внутренняя стороны 2³-l_m¸n-вакуумной протяженности (субконта и антисубконта) описываются совокупностью метрик

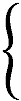ds^(–)2= (1+ v_1x v_2x/с²)c²dt² – v_1xdtdx + v_2xdxdt– dx² – dy² – dz²; (24.33)

ds⁽⁺⁾²= – (1+ v_3x v_4x/с²)c²dt² + v_3xdtdx – v_4xdxdt + dx² + dy² + dz², (24.34)

при этом не равные нулю усредненные нулевые компоненты метрического тензора (24.27) равны

g₀₀ ^(±) = (v_1x v_2x – v_3x v_4x)/2с², g₀₁ ^(±) = (v_3x – v_1x)/2, g₁₀ ^(±) = (v_2x – v_4x)/2 (24.35)

при (v_1x + v_3x)–(v_{2x +} v_4x) = 0. (24.36)

Это означает, что рассматриваемый 3-мерный локальный участок «вакуума» участвует в замысловатом движении вдоль оси х, при формальном соблюдении «вакуумного баланса» в отношении полного количества движения (24.32).

Рис. 24.1. Иллюстрация стечения «вакуума» к центру

его искривленной области

25. Предельная скорость перемещения слоев l_m¸n -вакуума

Зададимся вопросом: – «любая ли скорость может быть у сторон 2³-l_m¸n -вакуумной протяженности?» Рассмотрим данный вопрос на примере метрики (24.14)

ds^(–)2 = (1– v_x²/с²)c²dt² + 2v_xdxdt – dx² – dy²– dz², (25.1)

Выделим в (25.1) полный квадрат

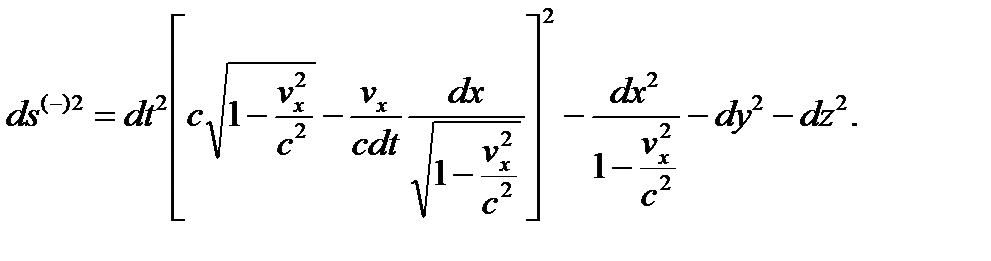(25.2)

и введем обозначения

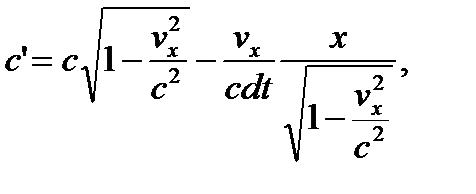
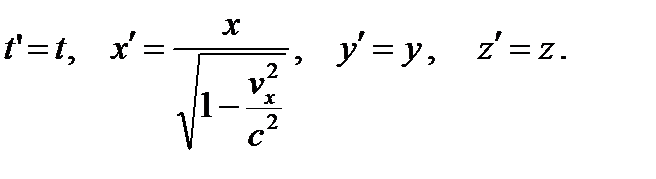(25.3)

В этих обозначениях метрика (25.1) принимает вид

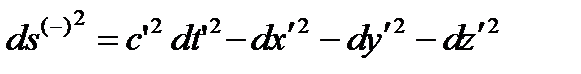. (25.4)

Физический смысл выражений (25.2) – (25.4) в корне отличается от аксиоматики СТО и ОТО А. Эйнштейна, поэтому требуется дополнительное разъяснение. Постулат Эйнштейна о постоянстве скорости света в вакууме остается неизменным. Но, если участок одной из сторон 2³-l_m¸n-вакуумной протяженности движется как целое со скоростью v_x [смотрите(24.12) – (24.15)], то для стороннего наблюдателя, находящегося на неподвижной РЛС (рис. 3.1), прямой луч света будет распространяться со скоростью

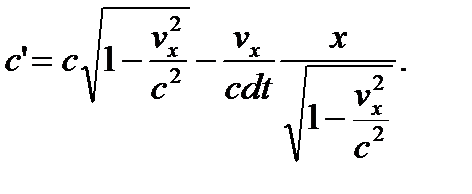(25.5)

Это подобно тому, как неподвижный наблюдатель измеряет скорость распространения волн, распространяющихся по движущейся воде реки. Такой наблюдатель обнаружит, что скорость распространения возмущений по поверхности воды зависит от скорости течения реки, тогда как относительно самой воды скорость распространения возмущений остается неизменной, и зависит только от свойств самой воды (ее плотности, температуры, примесей и т.д.).

Из выражений (25.3) следует, что, в случае (24.12) – (24.15), скорость распространения внешней стороны 2³-l_m¸n-вакуумной протяженности (субконта) не может превышать скорости света. При малых скоростях (v_x << c) для стороннего наблюдателя скорость c’ оказывается несколько меньшей скорости света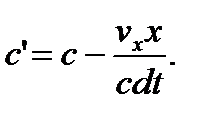

Таким образом, для случая (24.12) – (24.15), не смотря на то, что интерпретации математического аппарата АС и СТО отличаются, основные физические выводы остаются прежними.

Однако для случая (24.8) – (24.11) дело обстоит по-другому. Рассмотрим данный вариант внутри-вакуумных процессов на примере движения субконта, описываемого метрикой (24.10)

ds^(–)2 = (1+ v_x²/с²)c²dt²– dx² – dy² – dz². (25.6)

В этом случае введение обозначений

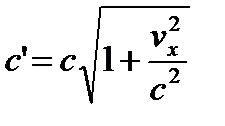
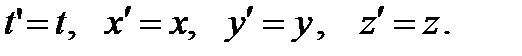(25.7)

приводит метрику (25.6) к инвариантному виду (25.4), но ни каких ограничений на встречные скорости движения v_x личины и изнанки субконта не возникает. Данное обстоятельство требует отдельного подробного рассмотрения, поскольку оно допускает возможность организации сверхсветовых внутри-вакуумных каналов связи.

26. Инертные свойства слоев l_m¸n -вакуума

Вернемся к рассмотрению метрик (24.2) и (24.3)

ds^{(+ – – –)2} = ds^(–)2 = c²dt² – dx² – dy² – dz² , (26.1)

ds^{(– + + +)2} = ds⁽⁺⁾² = – c²dt² + dx² + dy² + dz² . (26.2)

Вынесем величину с²dt² в правых частях этих метрикахза скобки

(26.3)

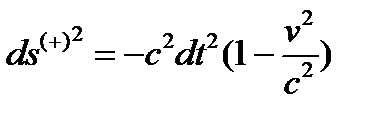, (26.4)

где v = (dx² +dy² +dz²)^1/2/dt = dl/dt – 3-мерная скорость.

Извлечем корень из двух сторон получившихся выражений (26.3) и (26.4). В результате, согласно условным обозначениям (24.4) – (24.7), получим

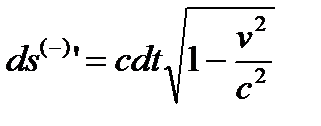– для личины субконта; (26.5)

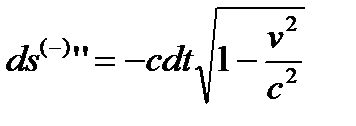– для изнанки субконта; (26.6)

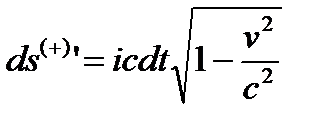– для личины антисубконта; (26.7)

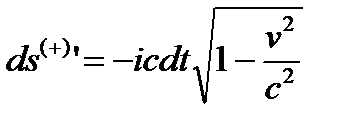– для изнанки антисубконта. (26.8)

Для примера рассмотрим 4-мерный вектор скорости (4-скорости) личины субконта [14]

u_i^(–)= dxⁱ /ds^(–)’. (26.9)

Подставляя (26.5)в (26.9), получим компоненты 4-скорости [14]

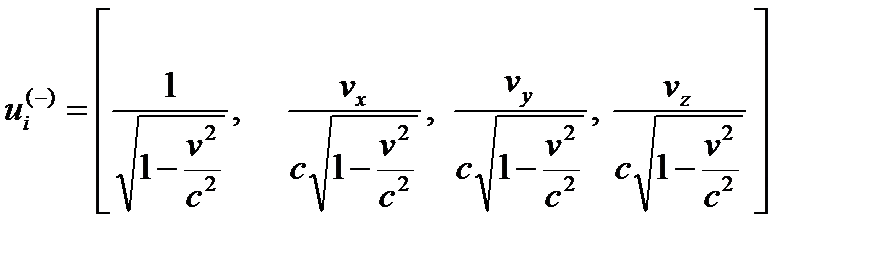, (26.10)

Пусть личина субконта двигается только в направлении оси х, тогда ее 4-скорость имеет компоненты

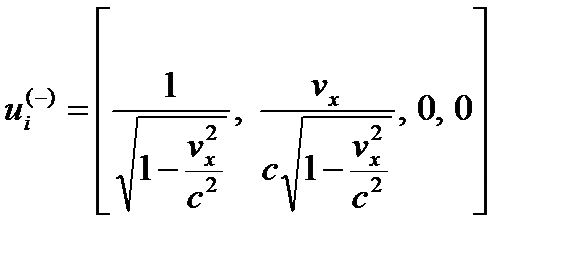. (26.11)

Определим теперь 4-ускорение личины субконта

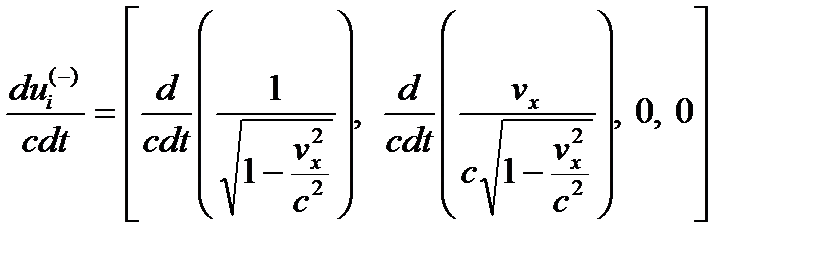. (26.12)

и рассмотрим только его х-составляющую

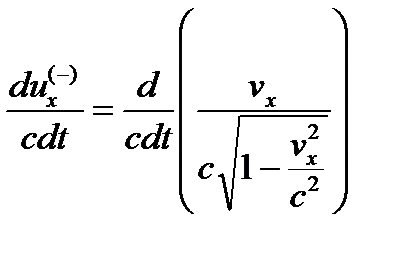, (26.13)

где величина

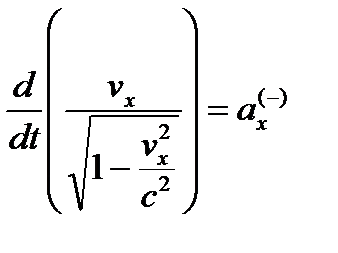, (26.14)

имеет размерность х-компоненты 3-мерного ускорения.

В левой части (26.14) выполним операцию дифференцирования

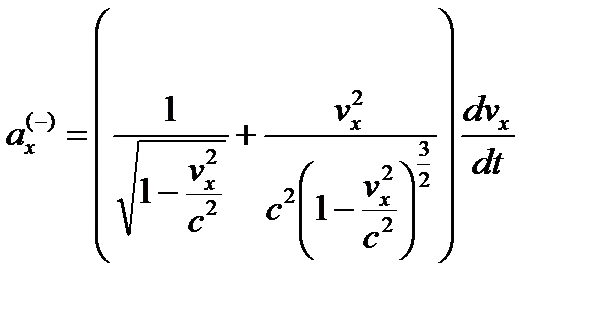, (26.15)

и введем обозначение

dv_x/dt = а_x^(–)' (26.16)

При этом выражение (26.15) принимает вид

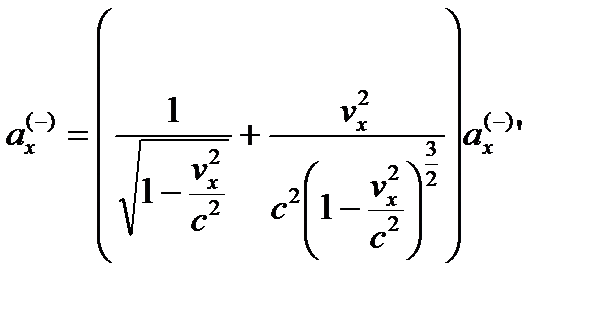, (26.17)

где a_x^(–) – актуальное ускорение участка личины субконта, учитывающее ее инертные свойства;

а_x^(–)' – идеальное ускорение того же участка личины субконта.

Представим выражение (26.16) в следующем виде

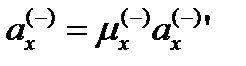, (26.18)

где

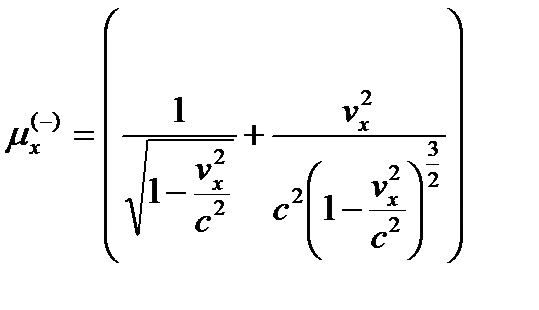(26.19)

– безразмерный коэффициент инертности, связывающий актуальное и идеальное ускорения изучаемого локального участка личины субконта, и показывающий как изменяется инертность (т.е. сопротивляемость изменению состояния движения) этого участка, при изменении скорости его движения.

Из выражения (26.19) следует, что при v_х = 0 коэффициент инертности m_х^(–)= 1 и 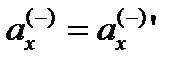. Это означает, что участок личины субконта не оказывает никакого сопротивления началу его движения. При приближении v_х к скорости света с коэффициент инертности m_х^(–) стремится к бесконечности, при этом дальнейшее ускорение личины субконта становится невозможным.

Выражение (26.18) является безмассовым аналогом второго закона Ньютона

F_x = ma_x¢, (26.20)

где F_x –компонента вектора силы; m – масса тела; a_x¢ – компонента его идеального ускорения.

Сравнивая (26.18) и (26.20), обнаруживаем, что в l_m¸n -вакуумной динамике безмассовый коэффициент инертности m_х^(–) локального участка личины субконта является аналогом плотности инертной массы сплошной среды в пост-ньютоновской физике.

Последовательной подстановкой интервалов (26.6) – (26.8) в выражение (26.9) аналогично могут быть получены коэффициенты инертности m_х^(–)¢¢, m_х⁽⁺⁾¢, m_х⁽⁺⁾¢¢ для трех остальных аффинных слоев 2³-l_m¸n -вакуумной протяженности. Общий коэффициент инертности локального участка 2³-l_m¸n -вакуумной протяженности является функцией от всех четырех коэффициентов инертности

m_х^(±)= f (m_х^(–)¢ , m_х^(–)¢¢, m_х⁽⁺⁾¢, m_х⁽⁺⁾¢¢ ) (26.20)

Вид этой функции будет определен в последующих статьях при изложении l_m¸n -вакуумной динамики.