Спектрально - стигнатурный анализ

Укажем на возможное применение Алгебры стигнатур для расширения возможностей спектрального анализа.

Напомним об известной в квантовой физике процедуре перехода от координатного представления к импульсному. Пусть имеется некоторая функция пространства и времени ρ(сt,x,y,z). Данную функцию представляют в виде произведения двух амплитуд:

ρ(сt,x,y,z) = φ(сt,x,y,z) φ(сt,x,y,z). (9.1)

Далее осуществляются два преобразования Фурье

, (9.2)

, (9.3)

где p = 2pη/l – обобщенная частота;

l – длина волны;

η – коэффициент пропорциональности (в квантовой механике η = ћ – постоянная Планка);

dΩ = dctdxdydz – элементарный 4-мерный объем;

ехр{i(w t – k× r)} = ехр{i(2p /l) (сt – x – y – z)} – прямая волна (правая спираль);(9.4)

ехр{i(–w t + k× r)} = ехр{i (2p /l) (– сt+x+y+z)} – обратная волна (левая спираль); (9.5)

ω – циклическая частота;

k – волновой вектор.

Импульсное (спектральное) представление функции ρ(сt,x,y,z) получается в результате произведения двух амплитуд (9.2) и (9.3)

. (9.6)

Вакуумный баланс данного спектрального представления достигается условием

(сt – x – y – z) + (– сt + x + y + z) = 0, (9.7)

с ранжирным аналогом (опр. 10.2)

{+ – – –}

{– + + +}

{0 0 0 0}. (9.8)

Теперь сформулируем основы спектрально-стигнатурного анализа.

По аналогии с процедурой (9.1) – (9.6) представим функцию ρ(сt,x,y,z) в виде произведения 8-и «амплитуд»:

ρ(сt,x,y,z)=φ₁(сt,x,y,z) φ₂(сt,x,y,z) φ₃(сt,x,y,z)×…×φ₈(сt,x,y,z) = . (9.9)

Вместо мнимой единицы i, присутствующей в интегралах (9.2) и (9.3), введем в рассмотрение восемь объектов ζ_r (где r = 1, 2, 3, … , 8), которые удовлетворяют следующим антикоммутативным соотношениям алгебры Клиффорда:

ζ_m ζ_k + ζ_k ζ_m = 0 при m ¹ k , ζ_m ζ_m = 1,(9.10)

или ζ_m ζ_k + ζ_k ζ_m = 2δ_km , (9.11)

где δ_km – символ Кронекера (δ_km= 0 при m ¹ k и δ_km= 1 при m = k).

Данным требованиям удовлетворяют, например, набор 8×8-матриц типа

(9.12)

В этом случае δ_km в (10.15) является единичной 8´8-матрицей:

(9.13)

Осуществим восемь преобразований Фурье,

, (9.14)

, (9.15)

, (9.16)

, (9.17)

, (9.18)

, (9.19)

, (9.20)

. (9.21)

где объекты ζ_m (9.12) выполняют функцию клиффордовых мнимых единиц.

Так же найдем восемь комплексно сопряженных им Фурье-образов:

, (9.22)

, (9.23)

, (9.24)

, (9.25)

, (9.26)

, (9.27)

, (9.28)

. (9.29)

По аналогии с выражением (9.6) спектрально - стигнатурное представление функции ρ(сt,x,y,z) получается в результате произведения восьми амплитуд (9.14) – (9.21) и восьми комплексно сопряженных им амплитуд (9.22) – (10.29).

. (9.30)

В этом случае имеет место 16 типов «цветных» волн (спиралей) с соответствующими стигнатурами (9.31)

ехр{ζ12p /l ( сt + x + y + z)} ехр{ζ22p /l (– сt –x – y + z)} ехр{ζ32p /l ( сt – x – y + z)} ехр{ζ42p /l (–сt – x + y – z)} ехр{ζ5 2p /l ( сt + x – y – z)} ехр{ζ62p /l (– сt + x – y – z)} ехр{ζ72p /l ( сt – x + y – z)} ехр{ζ82p /l (– сt+ x + y +z)} ехр{ζ1 2p /l (– сt –x – y – z)} ехр{ζ22p /l ( сt + x + y – z)} ехр{ζ32p /l (– сt + x + y – z)} ехр{ζ42p /l ( сt + x – y + z)} ехр (ζ5 2p /l(– сt – x + y + z)} ехр{ζ6 2p /l ( сt – x + y + z)} ехр{ζ72p /l (– сt + x– y + z)} ехр{ζ82p /l ( сt – x – y – z)}

{+ + + +} {– – – +} {+ – – +} {– – + –} {+ + – –} {– + – –} {+ – + –} {– + + +} {– – – –} {+ + + –} {– + + –} {+ + – +} {– – + +} {+ – + +} {– + – +} {+ – – –} {0 0 0 0}+

с ранжирным аналогом

{+ + + +} {– – – +} {+ – – +} {– – + –} {+ + – –} {– + – –} {+ – + –} {– + + +} {0 0 0 0)+

+ + + + + + + +

{– – – –} {+ + + –} {– + + –} {+ + – +} {– – + +} {+ – + +} {– + – +} {+ – – –} {0 0 0 0)+

= 0 = 0 = 0 = 0 (9.32) = 0 = 0 = 0 = 0 = 0 .

Таким образом, спектрально - стигнатурный анализ также остается сбалансированным относительно нуля.

В [2] показано, что попытка построения теории инвариантной относительно локальных фазовых вращений (т.е. локальных калибровочных преобразований) типа

e^{iα(– сt+ x + y +z)} = e ^{ζ12p /l (сt + x + y + z)}×е ^{ζ22p /l (– сt –x – y + z)} × е ^{ζ32p /l (сt – x – y + z)} ×е ^{ζ42p /l (–сt – x + y – z)} ×

× е ^{ζ5 2p /l (сt + x – y – z)} × е ^{ζ62p /l (– сt + x – y – z)} × е ^{ζ72p /l (сt – x + y – z)} , (9.33)

e^{iα( сt – x – y –z)} = e^{–ζ12p /l (сt + x + y + z)}×е^{–ζ22p /l (– сt –x – y + z)} × е^{–ζ32p /l (сt – x – y + z)} ×е^{–ζ42p /l (–сt – x + y – z)} ×

× е^{–ζ5 2p /l (сt + x – y – z)} × е^{–ζ62p /l (– сt + x – y – z)} × е ^{–ζ72p /l (сt – x + y – z)} (9.34)

приводит к развитию геометризированной вакуумной хромодинамики.

Алгебра сигнатур

Перейдем от аффинных геометрий к метрическим. Для примера рассмотрим аффинное (векторное) пространство с 4-базисом e_i⁽⁷⁾(e₀⁽⁷⁾,e₁⁽⁷⁾,e₂⁽⁷⁾,e₃⁽⁷⁾) (рис. 6.3) со стигнатурой {+ + + –}.

Зададим в этом пространстве 4-вектор

ds⁽⁷⁾ = e_i⁽⁷⁾dx_i⁽⁷⁾ = e₀⁽⁷⁾dx₀⁽⁷⁾+e₁⁽⁷⁾dx₁⁽⁷⁾+e₂⁽⁷⁾dx₂⁽⁷⁾+e₃⁽⁷⁾dx₃⁽⁷⁾, (10.1)

а) {+ + + +} б) {+ + + –} Рис. 10.1. Два 4-базиса с различными стигнатурами

где dx_i⁽⁷⁾ – это i-я проекция 4-вектора ds⁽⁷⁾ на ось x_i⁽⁷⁾, направление которой определяется базисным вектором e_i⁽⁷⁾.

Рассмотрим другой 4-вектор (10.2)

ds⁽⁵⁾ = e_i⁽⁵⁾dx_i⁽⁵⁾= e₀⁽⁵⁾dx₀⁽⁵⁾+e₁⁽⁵⁾dx₁⁽⁵⁾+e₂⁽⁵⁾dx₂⁽⁵⁾+ e₃⁽⁵⁾dx₃⁽⁵⁾,

заданный в аффинной системе отсчета x₀⁽⁵⁾, x₁⁽⁵⁾, x₂⁽⁵⁾, x₃⁽⁵⁾ с 4-базисом e_i⁽⁵⁾ (e₀⁽⁵⁾, e₁⁽⁵⁾, e₂⁽⁵⁾, e₃⁽⁵⁾) (рис. 6.3), со стигнатурой {+ + + +}.

Найдем скалярное произведение 4-векторов (10.1) и (10.2)

ds^{(5,7) 2} = ds⁽⁵⁾ds⁽⁷⁾ = e_i⁽⁵⁾e_j⁽⁷⁾dxⁱ dx^j = (10.3)

=e₀⁽⁵⁾e₀⁽⁷⁾dx₀dx₀ + e₁⁽⁵⁾e₀⁽⁷⁾dx₁dx₀ + e₂⁽⁵⁾e₀⁽⁷⁾dx₂dx₀ + e₃⁽⁵⁾e₀⁽⁷⁾dx₃dx₀ +

+ e₀⁽⁵⁾e₁⁽⁷⁾dx₀dx₁ + e₁⁽⁵⁾e₁⁽⁷⁾dx₁dx₁ + e₂⁽⁵⁾e₁⁽⁷⁾dx₂dx₁ + e₃⁽⁵⁾e₁⁽⁷⁾dx₃dx₁ +

+e₀⁽⁵⁾e₂⁽⁷⁾dx₀dx₂ + e₁⁽⁵⁾e₂⁽⁷⁾dx₁dx₂ + e₂⁽⁵⁾e₂⁽⁷⁾dx₂dx₂ + e₃⁽⁵⁾e₂⁽⁷⁾dx₃dx₂ +

+e₀⁽⁵⁾e₃⁽⁷⁾dx₀dx₃ + e₁⁽⁵⁾e₃⁽⁷⁾dx₁dx₃ + e₂⁽⁵⁾e₃⁽⁷⁾dx₂dx₃ + e₃⁽⁵⁾e₃⁽⁷⁾dx₃dx₃.

Для рассматриваемого случая, скалярные произведения базисных векторов e_i⁽⁵⁾e_j⁽⁷⁾ равны:

при i = j e₀⁽⁵⁾e₀⁽⁷⁾ = 1, e₁⁽⁵⁾e₁⁽⁷⁾ = 1, e₂⁽⁵⁾e₂⁽⁷⁾ = 1, e₃⁽⁵⁾e₃⁽⁷⁾ = –1, при i ≠ j e_i⁽⁵⁾e_j⁽⁷⁾ = 0.

При этом выражение (10.3) приобретает вид квадратичной формы

ds^(5,7)2 = dx₀dx₀ + dx₁dx₁ + dx₂dx₂ – dx₃dx₃ = dx₀² + dx₁² + dx₂² – dx₃² (10.4)

с сигнатурой (+ + + –).

Определение № 10.1 «Сигнатура» – упорядоченная совокупность знаков, стоящих перед соответствующими слагаемыми квадратичной формы (термин ОТО).

Чтобы определить сигнатуру метрического пространства с метрикой (10.4), вместо выполнения операции скалярного произведения векторов (10.3) можно просто перемножить стигнатуры 4-базисов, показанных на рис. 10.1:

{+ + + +}

{+ + + –} (10.5)

(+ + + –)_´

где умножение знаков производится по следующим правилам. В числителе (10.5) перемножаются знаки, находящиеся в одном столбце (в вертикальной шеренге), а результат такого перемножения записывается в знаменателе (под чертой) того же столбца. Умножение знаков осуществляется по следующим арифметическим правилам:

{+} ´ {+} = {+}; {–} ´ {+} = {–}; (10.6)

I {+} ´ {–} = {–}; {–} ´ {–} = {+},

для «вакуума»

{+} ´ {+} = {+}; {–} ´ {+} = {–}; (10.7)

H {+} ´ {–} = {+}; {–} ´ {–} = {–},

для некоммутативного «вакуума»

{+} ´ {+} = {–}; {–} ´ {+} = {–}; (10.8)

V {+} ´ {–} = {+}; {–} ´ {–} = {+},

для некоммутативного «антивакуума»

{+} ´ {+} = {–}; {–} ´ {+} = {+}; (10.9)

H {+} ´ {–} = {+}; {–} ´ {–} = {–}.

для «антивакуума»

В данной работе будет использоваться только правило умножения знаков (10.6) для «вакуума». Однако следует помнить, что в более последовательной теории должны присутствовать все четыре возможных типа «вакуумов» с правилами умножения (10.6) – (10.9) и четырьмя возможными «факториалами нуля» (по числу четырех букв Великого и Грозного Имени ВСЕВЫШНЕГО ה-ו-ה-י (H¢ V H I i) ): 0! = 1, 0! = –1, 0! = i, 0! = – i такими, что

1/4(0! + 0! + 0! + 0!) = (1–1) + i(1–1) =0 + i0 = Ѳ – комплексный истинный ноль, (10.10)

0! 0! 0! 0! = 0!⁴ = 1·(–1)·i·(–i) =– 1.

где под нулями могут также подразумеваются «расщепленные нули» типа (9.33) и (12.3).

На наличие четырех «вакуумов» с правилами умножения (10.6) – (10.9) было Указано через С.Г. Прохорова при участии В.П. Храмихина и М.Г. Иванова. Через С.Г. Прохорова так же было Передано, что данные «вакуумы» и «анти-вакуумы» являются, в некотором роде, опорами друг для друга в «Зыбкой Пустоте», т.е. обеспечивают стабильность Вакуума.

Поскольку арифметические действия в (10.5) выполняются по столбцам (шеренгам), будем называть подобные выражения «ранжирами» (ранжир – строй, порядок, шеренга).

Ранжирное деление стигнатур для «вакуума» с правилами умножения (10.6) определяется по арифметическим правилам действий со знаками:

{+} : {+} = {+}; {–}: {+} = {–}; (10.11)

{+} : {–} = {–}; {–}: {–} = {+}.

В этом случае в знаменателе стигнатурного ранжира будем ставить значок деления_, например, запись

{– + – +}

{+ + + –} (10.12)

(– + – –)_:

означает ранжирное деление по правилам (10.11).

Определение № 10.2 «Ранжир» – это выражение, определяющее арифметическое действие со стигнатурами аффинных (линейных) форм или со сигнатурами квадратичных форм. Знак после скобки в знаменателе ранжира (…)₊ – показывает какая операция производится со знаками в столбцах и/или строках ранжиров: (…)₊ - сложение, (…)_– –вычитание, (…)_: – деление, (…)_× – умножение.

Набор стигнатур (8.2):

(10.13)

образует две отдельные абелевы группы: по операции ранжирного умножения; и по операции ранжирного деления. Это свидетельствует о наличии глубинных симметрий в основаниях развиваемой здесь светогеометрии.

Если подобно тому, как это было проделано с векторами ds⁽⁵⁾ и ds⁽⁷⁾, попарно скалярно перемножить между собой вектора из всех 16-и аффинных пространств с 4-базисами, показанными на рис. 6.3, то получим 16´16 = 256 метрических 4-подпространств с метриками вида

ds^(аb)2 = e_i^(а)e_j^(b) dx^i(а)dx^j(b (10.14)

где a = 1,2,3,…, 16; b = 1,2,3,…, 16.

Сигнатуры этих 16 ´ 16 = 256 метрических 4-подпространств могут быть определены, подобно (10.8), ранжирными умножениями соответствующих стигнатур:

{+ – + +} {+ + + –} (+ – + –)´	{+ + + +} {+ – + –} (+ – + –)´	{– + + +} {+ + + –} (– + + –)´	{+ + + +} {– + + –} (– + + –)´
{+ – – +} {+ + + –} (+ – – –)´	{+ + – +} {– + + –} (– + – –)´	{– + + +} {– + + –} (+ + + –)´	{+ – + –} {+ – + –} (+ + + +)´
{+ – – –} {+ + + –} (+ – – +)´	{+ + – +} {– + – –} (– + + –)´	{– + – +} {– – + –} (+ – – –)´	{+ – + +} {+ – + –} (+ + + –)´
…	…	…	…
{+ + + –} {– – + –} (– – + +)´	{– + – –} {+ – + –} (– – – +)´	{– + + –} {+ – + –} (– – + –)´	{+ – – +} {– + + –} (– – – –)´

(10.15)

Точка О (рис. 6.1) одновременно принадлежит всем этим 256 метрическим 4 - подпространствам с сигнатурами (10.15), точнее она является местом их пересечения. В дальнейшем будет показано, что эти метрические 4-подпространства имеют различные топологии.

Набор из 256 метрических 4-подпространств (4-карт) образуют единый «атлас с пересечением в точке О, с общим числом математических измерений равным 256 ´ 4 = 1024. Поэтому развиваемый здесь математический аппарат Алгебры сигнатур можно отнести к разряду многомерных теорий. Но светогеометрия строится таким образом, чтобы все дополнительные математические измерения сводились к трем физическим измерениям «вакуума» и одному временному измерению, связанному со сторонним наблюдателем.

Подход Алгебры сигнатур во многом совпадает с локально-реперным (тетрадным) формализмом, который развивали Э. Картан, Р. Вайценбек, Т. Леви-Чивита, Г. Шипов [19] и часто использовал А. Эйнштейн в рамках дифференциальной геометрии с абсолютным параллелизмом.

Отличие Алгебры сигнатур от тетрадного метода в ОТО заключается в том, что в каждой точке 3-мерного многообразия («вакуума») задается не два 4-репера (тетрады) и одна метрика, например, ds^(аb)2 = e_i^(а)e_j^(b) dx^i(а)dx^j(b) с сигнатурой (+ – – –), или с сигнатурой (– + + +), а шестнадцать 4-базисов (или 4-реперов, или тетрад) (рис. 6.3), скалярные произведения которых образуют 256 метрик (10.14) с сигнатурами (10.15).

Рис. 11.1. Шестнадцать скалярных произведений 4-базисов, приводящих к метрикам с одинаковой сигнатурой (– + – +)

11. Первый этап компактификации дополнительных измерений

Одной из основных проблем любой многомерной теории является определение возможности компактификации (т. е. сворачивания) дополнительных математических измерений до наблюдаемых трех пространственных и одного временного измерения. Аналогичная задача стоит перед Алгеброй сигнатур.

Обратим внимание, что, например, 16 типов скалярных произведений 4-базисов, показанных на рис. 11.1, приводят к получению шестнадцати квадратичных форм (метрик) вида (10.10) ds^(аb)2 = e_i^(а)e_j^(b)dx^i(а)dx^j(b) с одинаковой сигнатурой (– + – +). Поэтому данные метрики можно усреднить.

Таким образом, можно выделить всего 256/16 = 16 типов метрических 4-пространств с метриками:

d сигнатурами.ких протяженностей с различными сигнатурами.s(+ + + +)2 = dx02 + dx12 + dx22 + dx32= 0 ds(– – – +)2 = – dx02 – dx12 – dx22 + dx32 = 0 ds(+ – – +)2 = dx02 – dx12 – dx22 + dx32 =0 ds(+– – –)2 = dx02 – dx12 – dx22 – dx32 = 0 ds(– – + –)2 = – dx02 – dx12 + dx22 – dx32 =0 ds(– + – –)2 = – dx02 + dx12 – dx22 – dx32 =0 ds(+ – + –)2 = dx02 – dx12 + dx22 – dx32 =0 ds(+ + – –)2 = dx02 + dx12 – dx22 – dx32 =0

ds(– – – – )2 = – dx02 – dx12 – dx22 – dx32 = 0 ds(+ + + –)2 = dx02 + dx12 + dx22 – dx32 =0 ds (– + + –)2 = – dx02 + dx12 + dx22 – dx32 = 0 ds(– + + +)2 = – dx02 +d x12 + dx22 + dx32 =0 ds(+ + – +)2 = dx02 + dx12 – dx22 + dx32 =0 ds(+ – + +)2 = dx02 – dx12+ dx22 + dx32 = 0 ds(– + – +)2 = – dx02 + dx12 – dx22 + dx32 =0 ds(– – + +)2 = – dx02 – dx12 + dx22 + dx32 = 0

с соответствующими сигнатурами (11.1)

.

В результате такого усреднения остается всего 4 ´ 16 = 64 математических измерений.

По классификации Феликса Клейна [12] метрические пространства с метриками (11.1) могут быть разбиты на три топологических класса:

1-й класс: 4-пространства, сигнатуры которых состоят из четырех одинаковых знаков [12]:

x₀² + x₁² +x₂² +x₃² = 0 (+ + + +); (11.2)

– x₀² – x₁² – x₂² – x₃² = 0 (– – – –)

– это так называемые нулевые метрические 4-пространства. У этих «пространств» имеется только одна действительная точка, находящаяся в начале светового конуса. Все остальные точки этих протяженностей являются мнимыми. По сути, первое из выражений (11.2) описывает не «протяженность», а единственную точку (или «белую» точку), а второе – единственную антиточку (или «черную» точку).

2-й класс: 4-пространства, сигнатуры которых состоят из двух положительных и двух отрицательных знаков [12]:

x₀² – x₁² – x₂² + x₃² = 0 (+ – – +);

x₀² + x₁² – x₂² – x₃² = 0 (+ + – –);

x₀² – x₁² + x₂² – x₃² = 0 (+ – + –);

– x₀² + x₁² + x₂² – x₃² = 0 (– + + –);

– x₀² – x₁² + x₂² + x₃² = 0 (– – + +)

– x₀² + x₁² – x₂² + x₃² = 0 (– + – +). (11.3)

- это различные варианты 4-мерных торов.

3-й класс: 4-пространства, сигнатуры которых состоят из трех одинаковых знаков и одного противоположного [12]:

– x₀² –x₁² – x₂² + x₃² = 0 (– – – +);

– x₀² – x₁² + x₂² – x₃² = 0 (– – + –);

– x₀² + x₁² – x₂² – x₃² = 0 (– + – –);

x₀² – x₁² – x₂² – x₃² = 0 (+ – – –);

x₀² + x₁² + x₂² – x₃² = 0 (+ + + –);

x₀² + x₁² – x₂² + x₃² = 0 (+ + – +);

x₀² – x₁² + x₂² + x₃² = 0 (+ – + +);

– x₀² + x₁² + x₂² + x₃² = 0 (– + + +). (11.4)

– это овальные 4-поверхности: а) эллипсоиды; б) эллиптические параболоиды; с) двуполостные гиперболоиды.

a) sign (+ +); б) sign (– +); в) sign (+ 0) x3 = x12 + x22x3 = x22 –x12 x3 = x12 параболическая седловидная U-образная поверхность поверхность поверхность   Рис. 11.2. Иллюстрация связи сигнатуры 2-мерного пространства с его топологией[12]

Упрощенная иллюстрация связи сигнатуры 2-мерного пространства с его топологией показана на рис. 11.2. Из этого рисунка видно, что сигнатура квадратичной формы однозначно связана с топологией, описываемой ею 2-мерной протяженности. Но не наоборот, топология протяженности – значительно более емкое понятие, чем сигнатура метрики.

Шестнадцать типов сигнатур (11.2) – (11.4), соответствующих 16 типам топологий метрических пространств, образуют матицу

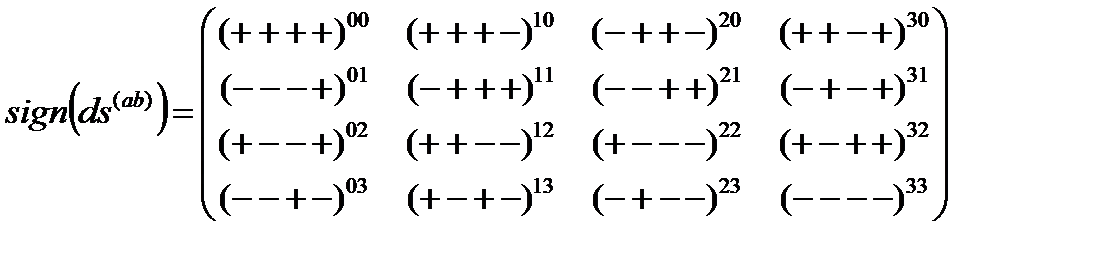, (11.5)

свойства которой совпадают со свойствами матрицы стигнатур (8.2).

Следует отметить, что по операции сложения сигнатуры (11.5) являются элементами более широкой группы, состоящей из 64 сигнатур: (11.6)

(+ + + +) (+ + + 0) (+ + 0 0) (+ 0 0 0) (0 0 0 0)

(0 + + +) (0 0 + +) (0 0 0 +) (+ 0 + +) (+ + 0 +)

(+ + + 0) (+ 0 + 0) (0 + 0 +) (+ 0 0 +) (0 + + 0)

(– – ––) (– – – 0) (– – 0 0) (– 0 0 0) (0 0 0 0)

(0 – ––) (0 0 – –) (0 0 0 –) (– 0 ––) (– – 0 –)

(– – – 0) (– 0 – 0) (0 – 0 –) (– 0 0 –) (0 – – 0)

… … … … …

(– + – 0) (– 0 + 0) (0 + 0 –) (– 0 0 +) (0 – + 0)

Рис. 11.4. Шахматная доска состоит из 32 белых и 32 черных клеток. В начале партии 16 белых фигур и 16 черных фигур

Определение № 11.1 «Шахматная аналогия» – это сходство Алгебры сигнатур с миром шахмат. У шахматной доски 8 ´ 8 = 64 клетки: 32 черные и 32 белые. Также в матрице сигнатур, (11.5) 64 знака, из них 32 плюса «+» и 32 минуса «–».

В начале партии на шахматной доске присутствует 32 шахматные фигуры: 16 белых и 16 черных (рис. 11.4). Так же в рамках Алгебры сигнатур в каждой точке l_m¸n-вакуума имеется шестнадцать 4-базисов, которые состоят из вращающихся векторов электрического поля (рис. 6.6), т.е. «фигур света»; и шестнадцать 4-базисов, связанных с углами кубической ячейки 3D-ландшафта (рис.6.2), т.е. «фигур тьмы».

Кроме того, сигнатуры (топологии) 16 типов метрических пространств (11.2) – (11.4) схожи с характеристиками шахматных фигур (рис. 11.5):

- двум нулевым топологиям (11.2) соответствуют «король» и «ферзь»;

- шести тороидальным топологиям (11.3) соответствуют три пары шахматных

фигур: 2 «офицера», 2 «коня» и 2-е «ладьи»;

-восемь овальным топологиям (11.4) соответствует восемь «пешек».

(+ – + +) пешка	(–– – +) пешка	(+ + – +) пешка	(+ –– –) пешка	(+ + + –) пешка	(– + + +) пешка	(–– + –) пешка	(– + – –) пешка
(–– + +) ладья	(+ – + –) конь	(– + + –) слон	(+ + + +) ферзь	(–– – –) король	(+ –– +) слон	(– + – +) конь	(+ + ––) ладья

Рис. 11.5. Сопоставление сигнатур (топологий) метрических пространств с шахматными фигурами

Сигнатура неявно входит в операции, выполняемые с помощь полностью антисимметричного единичного тензора (символа Леви-Чивиты) в n-мерном пространстве, который определен как

(11.7)

Для тензора справедливо следующее тождество с косвенным участием сигнатуры [23]

(11.8)

где S – количество знаков минус в сигнатуре метрики рассматриваемого пространства.

Определение № 11.2 Алгебра сигнатур (Алсигна) - (Ал (ЭЛЬ) – Б-Г, Гебор – Могущество, сигнатуры – знаки. Таким образом, Алсигна раскрывается как «Могущество ТВОРЦА, проявляющееся через систему Знаков». Основными знаками Алсигны являются буквы Иврита (Лашон а-Койдеш – Святого языка) – т.е. Азбука сигнатур. Основными алгоритмами Алсигны являются алгоритмы раскрытия Четырехбуквенного Имени ВСЕВЫШНЕГО (ТЕТРАГРАММАТОНА)

ה-ו-ה-י