Шестнадцать вращающихся 4-базисов

Вернемся к рассмотрению идеального (неискривленного) участка одного из l_m¸n - вакуумов (рис. 2.2, 6.1).

Рис. 6.1. Идеальная (неискривленная) 3D-«кристаллическая» решетка l_m¸n-вакуума, состоящая из

монохроматических лучей света с длиной волны l_m¸n. Ячейками такой решетки

являются идеальные кубики с длиной ребра e _m¸n ~ 10²·l_m¸n

В неискривленной области «вакуума» световые 3D-ландшафты отличаются друг от друга только длиной ребра кубической ячейки e _m¸n ~ 10²·l_m¸n, поэтому данный пункт относится к описанию любого из l_m¸n-вакуумов.

Подсчитаем, сколько ортогональных 3-базисов берут начало в центральной точке О исследуемого объема «вакуума» (рис. 6.1).

Определение № 6.1 Ортогональный 3-базис – это три взаимно перпендикулярных единичных вектора, выходящих из одной общей точки.

Если разнести 3-базисы из точки О (рис. 6.1) в разные стороны, то выяснится, что их 16 (рис. 6.2 а,б).

а) восемь 3-базисов б) восемь 3-антибазисов в) смежные кубические ячейки

Рис. 6.2. Шестнадцать 3-базисов в

центральной точке О изучаемого объема «вакуума»

Из них восемь 3-базисов относятся к самой кубической ячейке (рис. 6.2 а), а восемь противоположных им 3-антибазисов относятся к смежным кубическим ячейкам (рис. 6.2 б, в).

Любое движение в «вакууме» должно сопровождаться аналогичным антидвижением (это в рамках Алгебры сигнатур называется «вакуумным условием» (опр. 12.2). Поэтому если один 3-базис (вместе с кубической ячейкой) поворачивается по часовой стрелке (рис. 6.2 в), то это возможно, только если смежная кубическая ячейка (вместе с 3-антибазисом) аналогично поворачивается против часовой стрелки, поскольку в «вакууме» нет никакой точки опоры.

В связи с вышесказанным, удобно всем 3-базисам (рис. 6.2 а) добавить по четвертой оси времени, а восьми 3-антибазисам (рис. 6.2 б) добавить по четвертой противоположной анти-оси времени.

Таким образом, в рассматриваемой точке О l_m¸n-вакуума (рис. 6.1) имеется 8 + 8 = 16 ортогональных 4-базисов, показанных на рис. 6.3.

Рис.6.3. Шестнадцать 4-базисов с началом в точке О, полученных посредством добавления к восьми 3-базисам и восьми 3-антибазисам по четвертой аксиальной оси времени

Шестнадцать 4-базисов (рис. 6.3) могут быть получены в рамках радиолокационного метода зондирования локального участка «вакуума». В п. 3 было показано, что для определения метрико-динамических свойств «вакуума» в окрестности точки О, в эту точку должны приходить радиолокационные сигналы (монохроматические лучи света) не менее чем с трех взаимно перпендикулярных направлений (рис. 3.3).

Пусть в точку О приходят шесть монохроматических лучей света с круговой поляризацией (по два встречных луча света с трех взаимно перпендикулярных направлений, рис. 6.4).

y ZXYueG1sUEsFBgAAAAAEAAQA8wAAAPoFAAAAAA== " stroked="f">

Рис. 6.4. Поляризации лучей и антилучей света, приходящих в точку О с трех взаимно перпендикулярных направлений   Рис. 6.5. Круговая поляризации электромагнитной волны [13]   Рис.6.6. Два 3-базиса, состоящие из векторов электрическогополя Ex(+), Eу(+), Ez(+) и Ex(–), Eу(–), Ez(–) , вращающиеся в точке О во взаимно противоположных направлениях

Напомним, что поляризацией электромагнитной волны (или луча света) называется закон изменения направления вектора напряженности электрического поля Е, в плоскости перпендикулярной направлению распространения волны (или луча) (рис. 6.5) [13].

Для примера, рассмотрим два встречных луча света, распространяющихся навстречу друг другу вдоль оси Х (рис. 6.4). Пусть поляризация рассматриваемого луча света задается вектором электрическогополяE_x⁽⁺⁾, а поляризацияантилуча – вектором электрического поля E_x^(–). Эти вектора описываются комплексными выражениями [13]:

, (6.1)

, (6.2)

где E_zm⁽⁺⁾ – проекция вектора E_x⁽⁺⁾ на ось Z; E_ym⁽⁺⁾ – проекция вектора E_x⁽⁺⁾ на ось Y; E_zm^(–) – проекция вектора E_x^(–) на ось Z; E_ym^(–) – проекция вектора E_x^(–) на ось Y;

v – циклическая частота колебаний световой волны;

k_х – проекция волнового вектора на ось Х;

j_хz⁽⁺⁾,j_хy⁽⁺⁾–фазы ортогональных составляющих волны, распространяющейся в прямом направлении оси Х;

j_хz^(–),j_хy^(–)– фазы ортогональных составляющих волны, распространяющейся в противоположном направлении оси Х.

Из шести вращающихся векторов электрического поля, показанных на рис. 6.4, 6.6, можно составить 16 вращающихся 3-базисов. Из них: восемь 3 - базисов вращаются по часовой стрелке; а восемь других 3-базисов вращаются против часовой стрелки, как показано на рис. 6.3.

Кратко поясним, как вводился четвертая аксиальная ось в каждый 3-базис. Если частоты всех трех пробных монохроматических лучей, приходящих в исследуемуюточку О (рис. 6.4)с трех ортогональных направлений, одинаковы w_x = w_y = w_z, то их электрические вектора E_i^(±) в этой точке вращаются с одной и той же угловой скоростью

dj /dt = W =w_{x .} (6.3)

Вместе эти три вектора электрического поля E_i^(±) образуют ортогональный электрический 3-базис, постоянно вращающийся с угловой скоростью (6.3), откуда вытекает необходимость в ведении аксиальной оси времени j /W = t.

Таким образом, радиолокационный метод зондирования «вакуума» в окрестности точки О приводит к тем же шестнадцати 4-базисам, показанным на рис. 6.3. Но в этом случае реперными векторами данных 4-базисов являются вектора электрического поля E_i^(±).

Великое и Грозное Четырехбуквенное Имя ВСЕВЫШНЕГО ה-ו-ה-י(Йюд-Г’ей-Вав-Г’ей) многократно и разнообразно проявляется в структуре света.

Чтобы не употреблять Имя ВСЕВЫШНЕГО всуе, Алгебра сигнатур использует транслитерацию:

ה-ו-ה-י ≡ H¢ V H Ii(6.4)

где буква i соответствует коцу (острию) буквы י (Йюд), который соответствует пятому обобщающему элементу.

Имеет место полная аналогия Имени H'VHI с законами распространения света:

1) Число букв Имени и Антиимени совпадает с числом слагаемых в законе распространения света

H¢ V H Ii

ds⁽⁺⁾² = dz² + dy² + dx² – c²dt² =0 (6.5)

iI H V H¢

0 = c²dt² – dx² – dy² – dz² = ds^(–)2 (6.6)

2) Вектора эклектического Е и магнитного Н полей выражаются через 4 компоненты векторного потенциала А_i (j, А₁, А₂, А₃) º I H V H'

, . (6.7)

3) Волновое уравнение

, где k = 0, 1, 2, 3 º I H V H', (6.8)

описывающее распространение луча света (электромагнитной волны), допускает четыре вида решений (бегущих волн):

I со стигнатурой {– +};

H со стигнатурой {+ –}; (6.9)

V со стигнатурой {– –};

H¢ со стигнатурой {+ +},

гдеk – волновой вектор (|k | = 2p /l); I

r – вектор, задающий направление распространения луча света; H

w – циклическая частота гармонического колебания; V

а_i – амплитуда соответствующей волны. H¢

Субконт и антисубконт

Важным аспектом развиваемой здесь теории является утверждение, что объектом исследования является 3-мерный объем «вакуума» (рис. 2.2). Из этого постулата следует основная формула аффинной светогеометрии (4.2)

cdt = dl = (dx²+ dy² + dz²) ^½ = |idx + jdy +kdz| (7.1)

(гдеi, j, k–ортогональные единичные вектора), и основная формула метрической светогеометрии (4.3)

c²dt² = dx²+ dy² + dz². (7.2)

Преобразование тождества (7.2) приводит к системе из двух квадратичных форм:

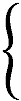ds^(–)2 = c²dt² – dx² – dy² – dz² = dx₀² – dx₁² – dx₂² – dx₃² = 0 с сигнатурой (+ – – –) (7.3)

ds⁽⁺⁾² = – c²dt² + dx² + dy² + dz² = – dx₀² + dx₁² + dx₂² + dx₃² = 0 с сигнатурой (– + + +) (7.4)

Из данной системы уравнений следует два «технических» вывода:

1. Квадратичные формы (7.3) и (7.4) можно условно интерпретировать как метрики двух 4-мерных «сторон» одного и того же 4 + 4 = 8 = 2³ - мерного метрического пространства, которое будем называть «2³-l_m¸n - вакуумной протяженностью».

Определение № 7.1 2^k-l_m¸n-вакуумная протяженность – это, вспомогательная логическая «конструкция», означающая пространство (с мощностью континуума) с 2^k математическими измерениями (где k = 3, 4, 5, … , ¥), которое «высвечивается» из «вакуума» посредством зондирования ее монохроматическими лучами света с длиной волны l_m¸n.

Самая простая 2³-l_m¸n -вакуумная протяженность имеет две «стороны»:

– 4-мерное пространство Минковского с метрикой (7.3) и сигнатурой (+ – – –);

– 4-мерное антипространство Минковского с метрикой (7.4) и сигнатурой (– + + +).

Рис. 7.1. Изогнутая двухстороння поверхность листа бумаги

Алгоритмы перехода от протяженных логических конструкций с 2^k математическими измерениями к 3 - мерному объему «вакуума» будут рассмотрены ниже.

Несмотря на то, 2³-l_m¸n -вакуумная протяженность являются чисто логической 4+4 = 8 - мерной конструкцией, из нее могут быть получены физические следствия. Поясним это на следующем 2 + 2 = 4 - мерном примере.

У листа бумаги (толщиной которого можно пренебречь) имеется две 2-мерных страницы (рис. 7.1). Поэтому лист бумаги можно рассматривать в качестве аналога 2 + 2 = 4-мерной протяженности.

Если лист бумаги не деформирован, то обе его «стороны» с точки зрения геометрии практически одинаковы. Однако если лист перегнуть, то с одной его 2-мерной стороны все ее элементарные площадки немного расширятся, а с другой сопряженной 2-мерной стороны – все элементарные площадки немного сожмутся.

Точно так же при искривлении локального участка «вакуума», в нем по необходимости (которая определяется «вакуумным условием») одновременно возникают, как локальные сжатия, так и локальные расширения, что автоматически учитывается как минимум «двусторонним» рассмотрением ее 4 + 4 = 8-мерной метрической протяженности. Таким образом, формальные математические приемы приводят к вполне осмысленным физическим следствиям.

Если учитывать толщину листа бумаги, то в качестве элемента рассмотрения должен быть уже элементарный кубик, находящийся между двумя сторонами листа. При этом, как будет показано ниже, потребуется рассмотрение континуальной протяженности с 4×16 = 8×8 = 64 математическими измерениями.

При еще более тонком рассмотрении понадобится уже 16 × 16 = 256-мерная протяженность, и т.д. до 2^k-мерного математического пространства (где k → ∞).

Таким образом, в светогеометрии «вакуума», развиваемой в рамках Алгебры сигнатур, имеется только 3 физических пространственных измерения «вакуума» и одно временное измерение, связанное со сторонним наблюдателем, а также 2^k математических (т.е. формальных или технических) измерений, где k = 3, 2, …, ∞ зависит от уровня рассмотрения исследуемого объема «вакуума».

Еще раз укажем на особенность времени в развиваемой здесь теории. В светогеометрии время не является атрибутом исследуемого участка «вакуума». Напомним, что в радиолокационном способе исследования метрико-динамических свойств локального участка «вакуума» (п. 3), интервал времени dt измеряется в приемо-передатчике радиолокационной установки (РЛУ) (рис. 3.1), который находится за пределами этого участка. Это соответствует часам стороннего наблюдателя, которые никакого отношения к изучаемому участку «вакуума» не имеют.

Когда задачу удается свести к двухстороннему рассмотрению, т.е. к исследованию 2³-l_m¸n-вакуумной протяженности, то предлагается ввести сокращенные условные обозначения:

Определение № 7.2 «Внешняя» сторона 2³-l_m¸n -вакуумной протяженности (или субконт) – это 4-мерная протяженность, локальные метрико-динамические свойства которой задаются метрикой

ds^{(+ – – –)2} = g_ij^(–)dxⁱdx^j с сигнатурой (+ – – –) (7.5)

где 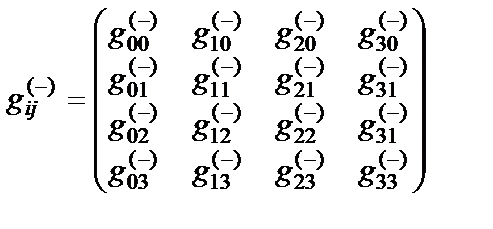(7.6)

- метрический тензор «внешней» стороны 2³-l_m¸n -вакуумной протяженности (или субконта).

В случае

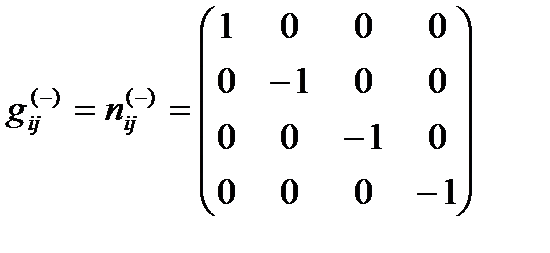(7.7)

«субконт» является синонимом 4-мерного пространства Минковского с метрикой (7.3) и сигнатурой (+ – – –);

Определение № 7.3 «Внутренняя» сторона 2³-l_m¸n -вакуумной протяженности (или антисубконт) – это 4-мерная протяженность, локальные метрико-динамические свойства которой задаются метрикой

ds^{(– + + +)2} = g_ij⁽⁺⁾dxⁱdx^j, с сигнатурой (– + + +) (7.8)

где 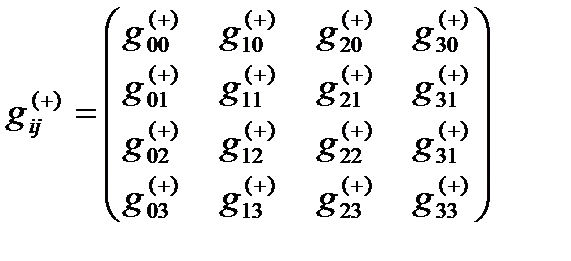(7.9)

- метрический тензор «внешней» стороны 2³-l_m¸n-вакуумной протяженности (или антисубконта).

В случае

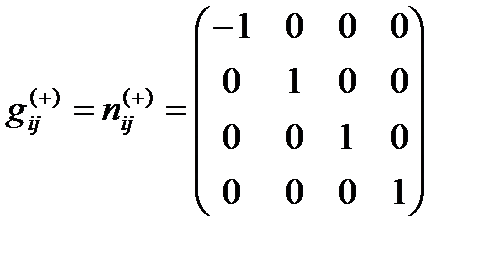(7.10)

«антисубконт» является синонимом 4-мерного антипространства Минковского с метрикой (7.4) и сигнатурой (– + + +).

В определениях 7.2 и 7.3 для сокращения изложения ведены два вспомогательных понятия:

Определение № 7.4 «Субконт» (сокращ. от «субстанциональный континуум») – это умозрительная сплошная упруго-пластическая 4-мерная псевдосреда, локальные метрико - динамические свойства которой задаются метрикой (7.6).

Определение № 7.5 «Антисубконт» (сокращ. от «антисубстанциональный континуум») – это умозрительная сплошная упруго-пластическая 4-мерная псевдосреда, локальные метрико-динамические свойства которой задаются метрикой (7.8).

Понятия «субконт» и «антисубконт» не имеют отношения к реальности. Это вспомогательные 4-мерные псевдосреды, которые являются синонимами соответственно «внешней» и «внутренней» сторон 2³-l_m¸n -вакуумной протяженности, и вводятся они только для удобства восприятия ряда 3-мерных упруго-пластических процессов, протекающих в «вакууме».

Реальным объектом в Алгебре сигнатур является только 3-мерный объем «вакуума». Все многомерные математические выкладки сводятся к вычислению только 3-мерных физических величин, характеризующих метрико-динамическое состояние локального или глобального участка «вакуума».

Алгебра стигнатур

Выше были рассмотрены физические основы светогеометрии «вакуума». Далее будут в основном затрагиваться формальные геометрические и математические аспекты данной теории.

Как бы далее ни усложнялся формальный математический аппарат Алгебры сигнатур, следует помнить, что геодезическими линиями исследуемого 3D-ландшафта (или l_m¸n-вакуума) являются монохроматические бесконечно тонкие лучи света с длиной волны l_m¸n. При этом основным «предметом» рассмотрения является бесконечно малая 3-мерная кубическая ячейка l_m¸n-вакуума в окрестности точки О (рис. 6.1, 6.2), с каждым углом которой связано по два вращающихся 4-базиса, показанных на рис. 6.3.

Каждый из этих шестнадцати 4-базисов задает направление осей 4-мерного аффинного пространства со своей особой характеристикой, которую будем называть «стигнатура».

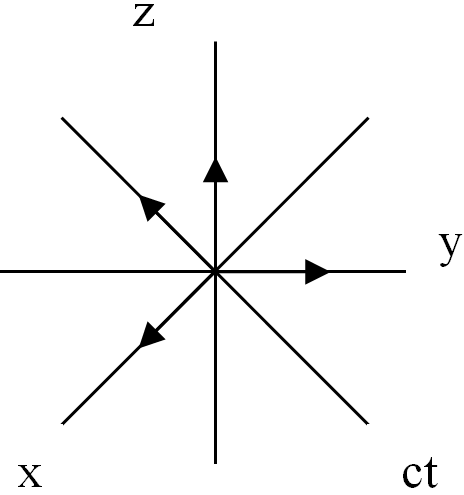Рис. 8.1. База со стигнатурой {+ + + +}

Чтобы ввести характеристику «стигнатура» аффинного пространства, сначала определим понятие «база». Выберем из 16-и 4-базисов, показанных на рис. 6.3, в качестве «базы» пятый 4-базис e_i⁽⁵⁾(e₀⁽⁵⁾,e₁⁽⁵⁾,e₂⁽⁵⁾,e₃⁽⁵⁾) (рис. 8.1) и условно примем, что направления всех его единичных базисных векторов положительны

e_i⁽⁵⁾(e₀⁽⁵⁾,e₁⁽⁵⁾,e₂⁽⁵⁾,e₃⁽⁵⁾) = (+1, +1,+ 1, +1) ® {+ + + +}. (8.1)

Здесь введено сокращенное обозначение {+ + + +}, которое в дальнейшем будем называть «стигнатурой» аффинного (векторного) пространства, задаваемого 4-базисом e⁽⁵⁾.

Определение № 8.1 «База» – это один из 16-и 4-базисов, показанных на рис. 6.3, направления всех 4-х единичных векторов которого условно приняты положительными, поэтому стигнатура базы всегда {+ + + +}.

Определение № 8.2 «Стигнатура» 4-базиса – это совокупность знаков, соответствующих направлениям базисных векторов по отношению к направлениям базисных векторов «базы».

Относительно произвольно выбранной «базы» (т. е. 4-базисаe⁽⁵⁾) оси всех остальных 4-базисов, показанных на рис. 6.3, имеют следующие знаки:

Таблица 8.1

ei(1) (e0(1), e1(1), e2(1), e3(1)) = = (1, 1, –1, 1) ® {+ + – +}   ei(2) (e0(2), e1(2), e2(2), e3(2)) = = (1, –1, –1, –1) ® {+ – – –}   ei(3) (e0(3), e1(3), e2(3), e3(3)) = = (1, 1, –1, –1) ® {+ + – –}   ei(4) (e0(4), e1(4), e2(4), e3(4)) = = (1, –1, –1, 1) ® {+ – – +}   ei(5) (e0(5), e1(5), e2(5), e3(5)) = = (1, 1, 1, 1) ® {+ + + +}   ei(6) (e0(6), e1(6), e2(6), e3(6)) = = (1, –1, 1, –1) ® {+ – + –}   ei(7) (e0(7), e1(7), e2(7), e3(7)) = = (1, 1, 1, –1) ® {+ + + –}   ei(8) (e0(8), e1(8), e2(8), e3(8)) = = (1, –1, 1, 1) ® {+ – + +}

ei(9) (e0(9), e1(9), e2(9), e3(9)) = = (–1, 1, –1, 1) ® {– + – +}   ei(10) (e0(10), e1(10), e2(10), e3(10)) = = (–1, 1, –1, –1) ® {– – – –}   ei(11) (e0(11), e1(11), e2(11), e3(11)) = = (–1, 1, –1, –1) ® {– + – –}   ei(12) (e0(12), e1(12), e2(12), e3(12)) = = (–1, –1, –1, 1) ® {– – – +}   ei(13) (e0(13), e1(13), e2(13), e3(13)) = = (–1, 1, 1, 1) ® {– + + +}   ei(14) (e0(14), e1(14), e2(14), e3(14)) = = (–1, –1, 1, –1) ® {– – + –}   ei(15) (e0(15), e1(15), e2(15), e3(15)) = = (–1, 1, 1 –1) ® {– + + –}   ei(16) (e0(16), e1(16), e2(16), e3(16)) = = (–1, –1, 1, 1) ® {– – + +}

Все стигнатуры, приведенные в табл. 8.1, объединяются в 16-компонентную матрицу:

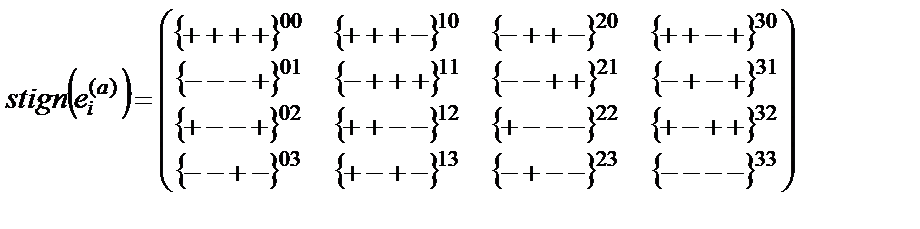. (8.2)

Эта матрица представляет собой отдельный математический объект, обладающий уникальными свойствами. Перечислим некоторые из них:

1. Сумма всех 16-и стигнатур (8.2) равна нулевой стигнатуре

{+ + – +} + {+ – – –} + {+ + – –} + {+ – – +} +

+ {+ + + +} + {+ – + –} + {+ + + –} + {+ – + +} + (8.3)

+ {– + – +} + {– – – – } + {– + – –} + {– – – +} +

+ {– + + +} + {– – + –} + {– + + –} + {– – + +} = {0000}.

2. Сумма всех 64 знаков, входящих в матрицу (8.2) равна нулю (32 «+» + 32 «–» = 0).

3. Возможны четыре бинарные комбинации знаков:

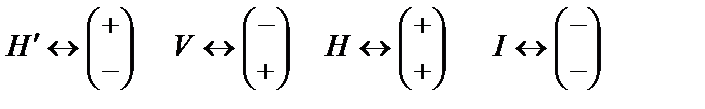, (8.4)

или в транспонированном виде

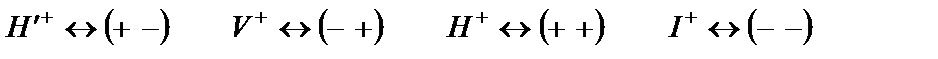. (8.5)

Всевозможные сочетания данных бинарных комбинаций знаков образуют 16 вариантов стигнатур:

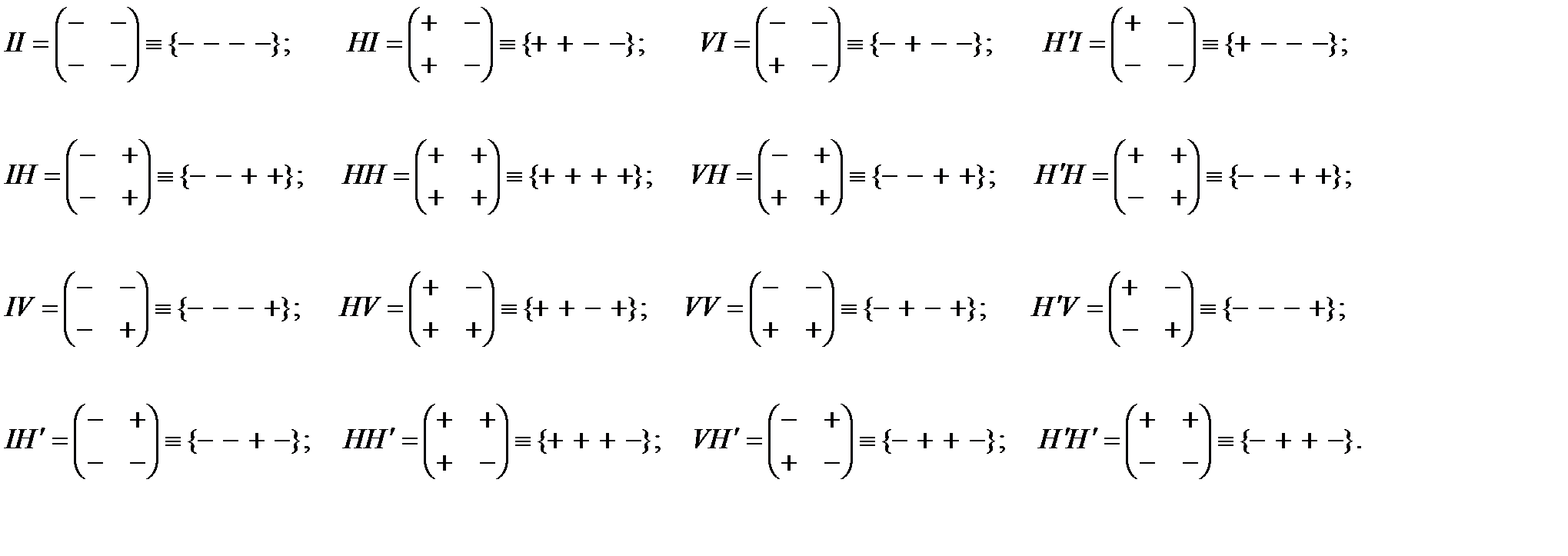(8.6)

Светогеометрия «вакуума» строится на основании Алгоритмов Раскрытия Великого и Грозного Имени ВСЕВЫШНЕГО ה-ו-ה-י (Йюд-Г’ей-Вав-Г’ей) [4].

Одна из форм раскрытия Имени ה-ו-ה-י (H¢ V H I i) является «Древо десяти Сфирот», которое можно получить путем возведения в кронекеров квадрат двурядной матрицы:

(8.6b)

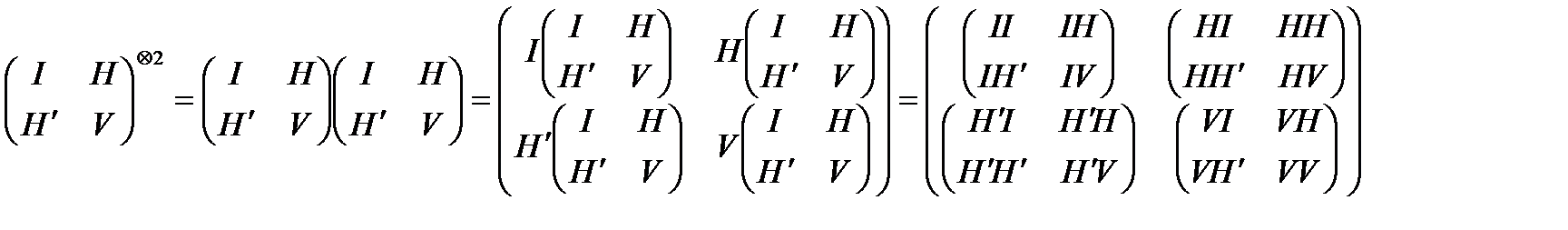
Компоненты данной матрицы соответствуют 10 Сфирот

i (коц) II Кетер

IHH Хохма

H VV Бина (8.6c)

V IV, IH, IH¢, VH, VH¢, HH¢ Тиферет*

VI, HI, H¢I, HV, H¢V, H¢H

H¢H¢H¢ Малхут

где Тиферет* состоит из шести Сфирот:

Хесед (IV = VI) Гвуга (IH = HI) Тиферет (IH¢ = H¢I) (8.6d)

Нецах (VH=HV) Ход (VH¢ = VH¢) Йесод (HH¢ = H¢H)

4. Кронекеров квадрат двурядной матрицы бинарных стигнатур образует матрицу 16 стигнатур (8.2):

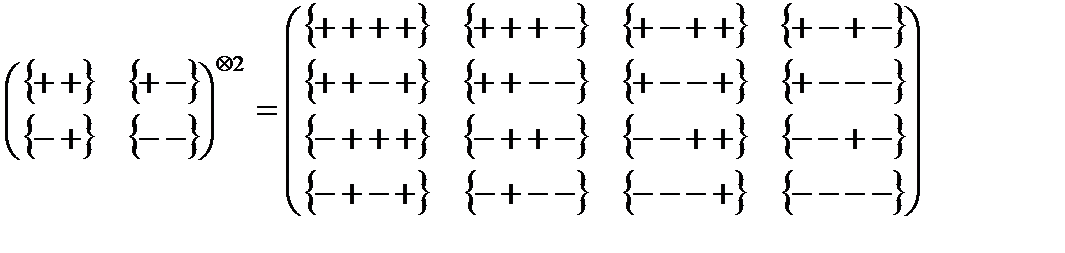(8.7)

где Ä – символ, означающий кронекерово умножение.

5. Если матрицам (8.6) вернуть исходные единицы, то получим двурядные матицы

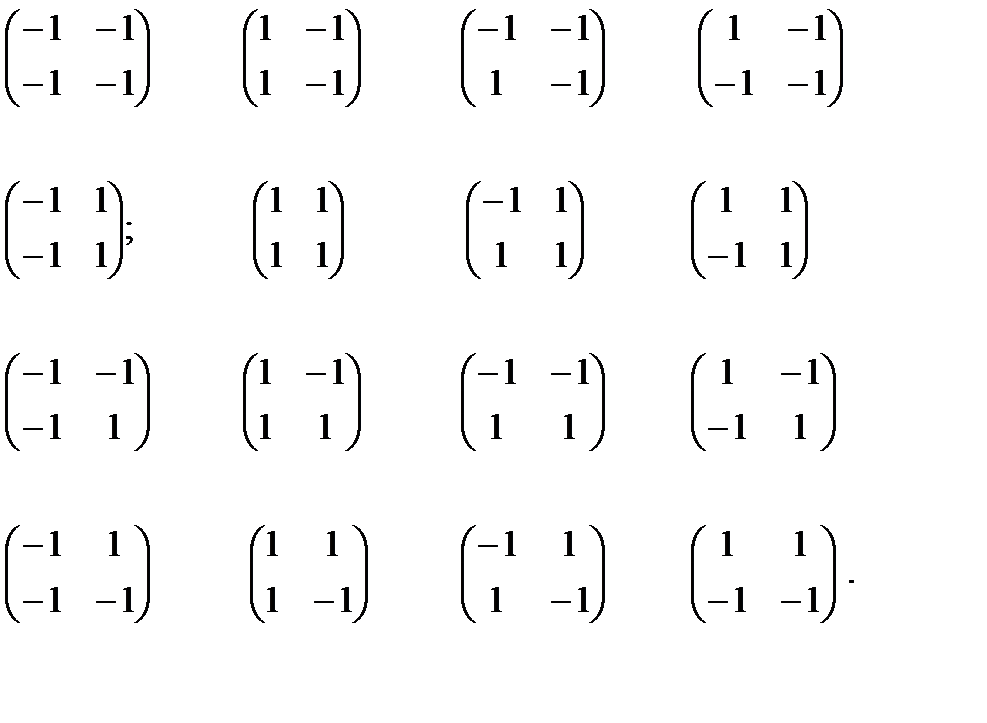(8.8)

Из них восемь:

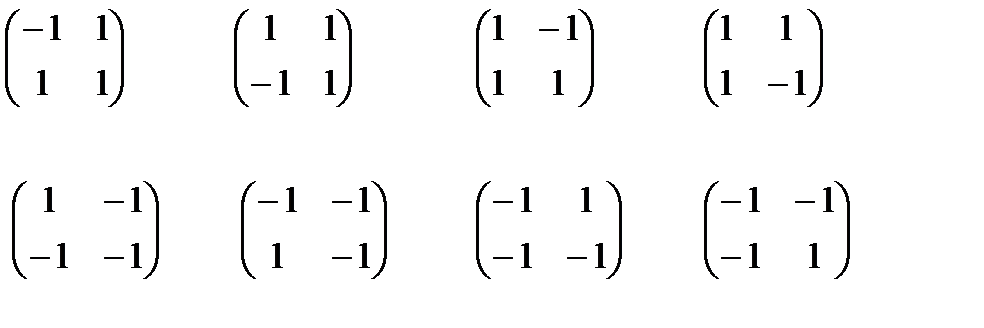(8.9)

(8.10)

являются матрицами Адамара, т.к. они удовлетворяют условию

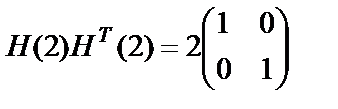. (8.11)

При возведении в кронекеровы степени любой из матриц (8.9, 8.10) вновь получаются матрицы Адамара Н(n), удовлетворяющие условию:

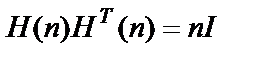, (8.12)

где I – диагональная единичная матрица размерности n:

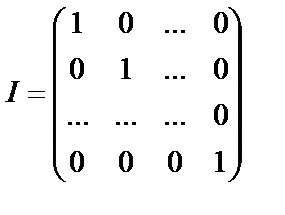. (8.13)

Например,

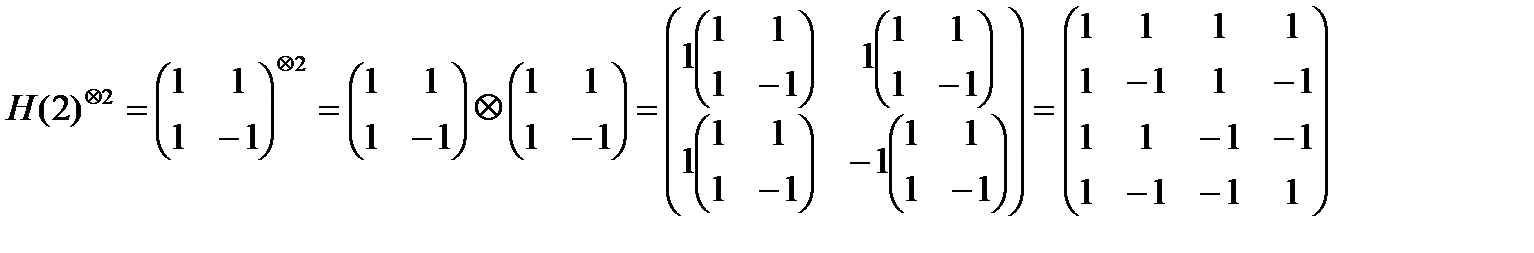, (8.14)

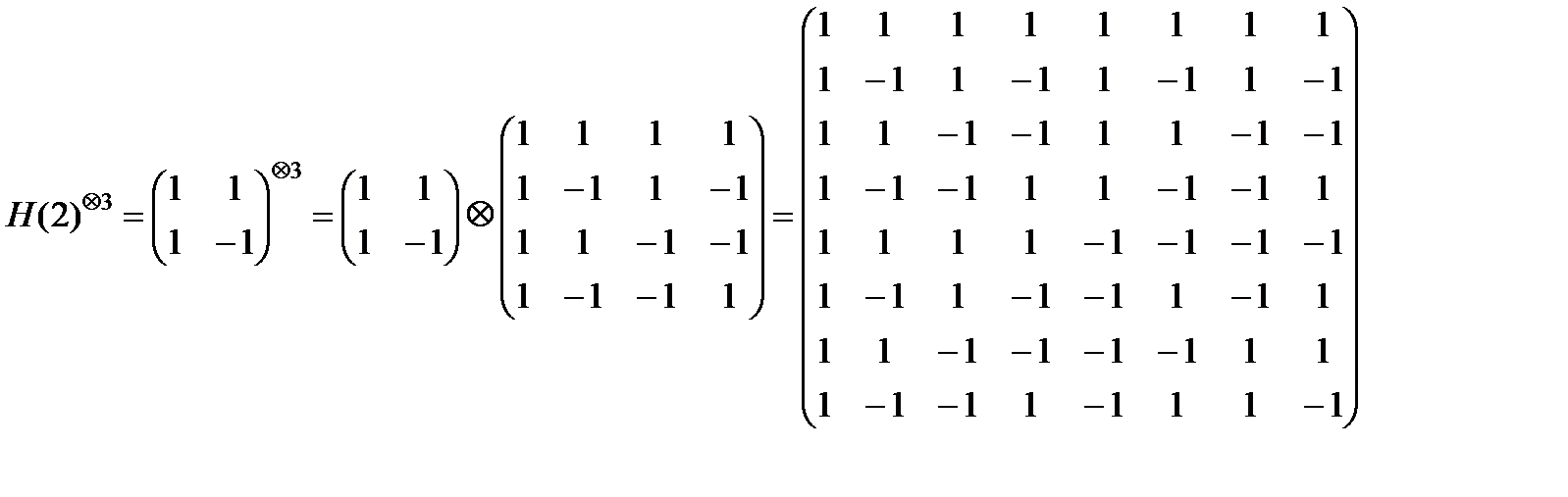(8.15)

и так далее по алгоритму

Н(2)^Äk = Н(2^k) = Н(2)Ä Н(2)^Äk-1 = Н(2)Ä Н(2^k-1), (8.16)

Благодаря различным уникальным свойствам матрицы Адамара Н(n) получили широкое применение во многих областях науки. В теории кодирования матрицы Н(n) используют для разработки помехоустойчивых кодов с исправлением ошибок, в теории планирования они применяются для составления блок-схем. Матрицы Адамара оказались полезными для расшифровки генетического кода, т. е. для изучения спиральной структуры молекулы ДНК.

5. «База», показанная на рис. 8.1, выбрана условно. В случае выбора другой «базы» из 4-базисов, показанных на рис. 6.3, знаки в матрице стигнатур (8.2) поменяются местами, но ее свойства не изменятся. С этим видом инвариантности связаны отдельные свойства l_m¸n -вакуума, которые будут рассмотрены позже.

6. Шестнадцати 4-базисам, приведенным на рис. 6.3 и в табл. 8.1, соответствуют 16 типам «цветных» кватернионов (8.17)

z1 = x0 + ix1 + jx2 + kx3 {+ + + +}   z2 = –x0 –ix1 – jx2+ kx3 {– – – +}   z3 = x0 – ix1 – jx2+ kx3 {+ – – +}   z4 = –x0 – ix1+ jx2–kx3 {– – + –}   z5 = x0 +ix1 – jx2 –kx3 {+ + – –}   z6 = –x0 + ix1 – jx2–kx3 {– + – –}   z7 = x0 – ix1+ jx2 – kx3 {+ – + –}   z8 = –x0+ix1 + jx2 + kdx3 {– + + +}

{– – – –} z9 = –x0 – ix1 – jx2 – kx3   {+ + + –} z10 = x0 + ix1 + jx2 – kx3   {– + + –} z11= – x0 + ix1 + jx2 – kx3   {+ + – +} z12= x0 + ix1 – jx2 + kx3   {– – + +} z13= –x0 – ix1 + jx2+ kx3   {+ – + +} z14= x0 – ix1 +jx2+ kx3   {– + – +} z15 = –x0 + ix1– jx2+ kx3   {+ – – –} z16 = x0 – ix1 – jx2 – kx3

В [2] показано, что «цвета» кватернионов соответствуют «цветам» квантовой хромодинамики.

Прямым вычислением легко убедиться, что сумма всех 16 типов «цветных» кватернионов (8.17) равна нулю

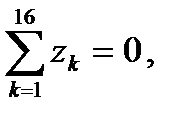(8.18)

т. е. суперпозиция всех типов «цветных» кватернионов сбалансирована относительно нуля.

В теории спиноров кватернионы являются одним из разновидностей клиффордовых агрегатов [16]:

а = а₀ + e₁а₁ + e₂а₂ + e₃а₃, (8.19)

где а_i – вещественные числа; e_i – орты, подчиняющиеся правилу умножения

1e_i=е_i1, e_ie_k= – d_ik 1 + e_ikne_n, (8.20)

где d_ik и e_ikn – символы Кронекера и Леви-Чивиты (i, k, n = 1,2,3).

7. Матрица стигнатур (8.2) может быть представлена в виде суммы диагональной и антисимметричной матриц

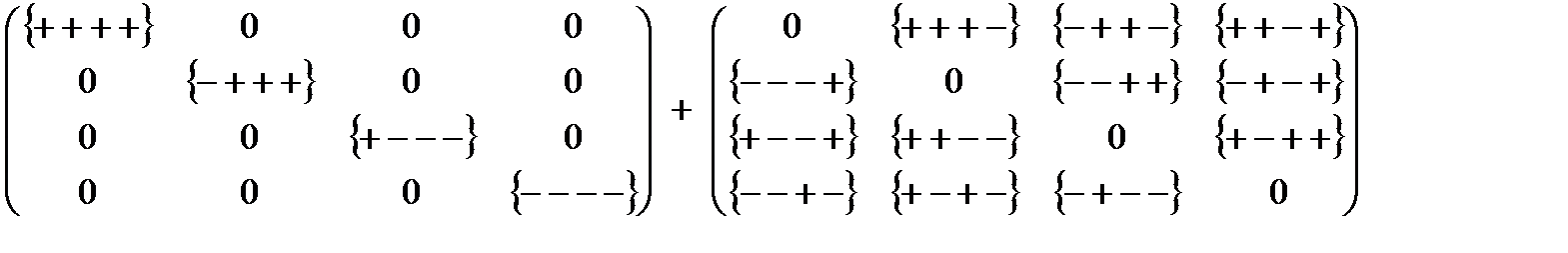(8.21)

8. Пусть задана матрица, составленная из четырех элементов a, b, c, d

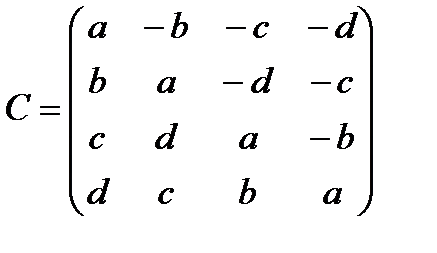, (8.22)

Произведение матрицы (8.22) с одной из матиц Адамара (8.14) приводи к матице, компонентами которой являются линейные формы с различными стигнатурами (8.23)