Принцип суперпозиции. Интерференция волн

Принцип суперпозиции (наложения) волн: при распространении в среде нескольких волн каждая из них распространяется так, как будто другие волны отсутствуют, а результирующее смещение частицы среды в любой момент времени равно геометрической сумме смещений, которые получают частицы каждой волны.

Интерференция волн– наложение двух (или нескольких) когерентных волн, в результате чего происходит усиление или ослабление результирующей волны в зависимости от соотношения между фазами этих волн.

Когерентными называются волны одного направления одинаковой частоты и постоянной разности фаз.

Рассмотрим наложение двух когерентных волн, возбуждаемых точечными источниками (для простоты начальные фазы ):

.

Разность фаз этих колебаний равна

, (115)

где - разность хода волн, - длина волны.

1) если колебания происходят в одинаковой фазе, т.е. ( , (116)

то наблюдается максимум интерференции. Приравниваем (115) и (116):

.

Получаем условие максимума при интерференции:

( . (117)

В этом случае .

2) если колебания происходят в противофазе, т.е.

( , (118)

то наблюдается минимум интерференции. Приравниваем (115) и (117):

.

Получаем условие минимумапри интерференции:

( . (118)

В этом случае .

Стоячие волны

Особым случаем интерференции являются стоячие волны – это волны, образующиеся при наложении двух волн одинаковой частоты и амплитуды, распространяющихся навстречу друг другу.

Такой случай можно реализовать, заставив бегущую волну отразиться от преграды (рис. 24).

Уравнения падающей и отражённой волн имеют вид:

.

Сложив эти уравнения, используя тригонометрические преобразования, получаем уравнение стоячей волны:

, (119)

где амплитуда стоячей волны:

. (120)

Из выражения (120) видно, что амплитуда стоячей волны

. (121)

Точки, в которых амплитуды бегущей и отражённой волны складываются, называются пучностями( ).

Точки, в которых амплитуда равна нулю, называются узлами( ). Эти точки колебаний не совершают.

Пучность образуется в тех точках, где колебания бегущей и отражённой волн происходят в одинаковой фазе, т.е. ( ). Следовательно, координаты пучностей:

( ) . (122)

Узлы образуются там, где колебания происходят в противофазах, т.е. ( ). Следовательно, координаты узлов:

( ). (123)

Длиной стоячей волны называется расстояние между пучностями или узлами: .

Таким образом, длина стоячей волныравна половине длины складываемых волн:

. (124)

Стоячая волна не переносит энергии, т.к. энергия переносится в равных количествах бегущей и отражённой волнами.

Электромагнитные волны

Из уравнений Максвелла вытекает существование электромагнитных волн– переменного электромагнитного поля, распространяющегося в вакууме с конечной скоростью .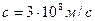

Можно показать, что для однородной и изотропной среды вдали от зарядов и токов, создающих электромагнитное поле, из уравнений Максвелла следует, что векторы напряжённостей электрического и магнитного полей удовлетворяют уравнениям:

(124)

(125)

где 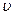- фазовая скорость.

Всякая функция, удовлетворяющая уравнениям (124) и (125), описывает некоторую волну. Следовательно, электромагнитные поля действительно могут существовать в виде электромагнитных волн. Фазовая скорость электромагнитных волн определяется выражением

, (126)

где - скорость электромагнитной волны в вакууме, , - электрическая и магнитная постоянные, , - диэлектрическая и магнитная проницаемости среды, - показатель преломления среды.

В вакууме ( ) , . Поскольку скорость электромагнитной волны в среде всегда меньше, чем в вакууме, т.е. .

Длина электромагнитной волны

.

Следствием теории Максвелла является поперечность электромагнитных волн: векторы и взаимно перпендикулярны и лежат в плоскости, перпендикулярной вектору скорости распространения волны, причём векторы , и образуют правовинтовую систему (рис. 25). Из уравнений Максвелла следует также, что в электромагнитной волне векторы и всегда колеблются в одинаковых фазах, причём мгновенные значения напряжённостей электрического и магнитного полей электромагнитной волны в любой точке связаны соотношением:

. (127)

Источником электромагнитных волн может быть любой колебательный контур или проводник, по которому течёт переменный ток. Однако излучающая способность источника определяется его формой, размерами и частотой колебаний. Чтобы излучение играло заметную роль, необходимо увеличить объём пространства, в котором электромагнитное поле создаётся. Поэтому для получения электромагнитных волн непригодны закрытые колебательные контуры (рис. 17), т.к. в них электрическое поле сосредоточено между обкладками конденсатора, а магнитное – внутри катушки индуктивности.

Герц в своих опытах, уменьшая число витков катушки и площадь пластин конденсатора, а также раздвигая их, совершил переход от закрытого колебательного контура к открытому колебательному контуру (вибратору Герца), представляющему собой два стержня, разделённых искровым промежутком. Колебания в такой системе поддерживаются за счёт источника э.д.с., подключённого к обкладкам конденсатора, а искровой промежуток применяется для того, чтобы увеличить разность потенциалов, до которой первоначально заряжаются обкладки.

Возможность обнаружения электромагнитных волн указывает на то, что они переносят энергию. Объёмная плотность энергии электромагнитной волны равна сумме плотностей энергий электрического и магнитного полей:

. (128)

Учитывая выражение (127), получим, что плотности электрического и магнитного полей в каждый момент времени одинаковы, т.е. . Поэтому

Умножив плотность энергии на скорость распространения волны в среде из формулы (126), получим плотность потока энергии, т.е. энергию, переносимую волной за единицу времени через единичную площадку, расположенную перпендикулярно к направлению распространения волны:

.

Так как векторы и взаимно перпендикулярны и образуют с направлением распространения волны правовинтовую систему, то направление вектора совпадает с направлением переноса энергии, а модуль этого вектора равен . Следовательно, вектор плотности потока электромагнитной энергии (вектор Умова-Пойнтинга):

.

Шкала электромагнитных волн

-радиоволны;

( - сверхвысокочастотное излучение (СВЧ);

( - инфракрасное излучение (ИК);

( - видимый свет;

( ) – ультрафиолетовое излучение (УФ);

- рентгеновское излучение;

- -излучение.

ЛИТЕРАТУРА

1. Савельев И.В. Курс общей физики (т.1). М.: Наука, СПб.: Лань, 2006.

2. Савельев И.В. Курс общей физики (т.3). М.: Наука, СПб.: Лань, 2006.

3. Трофимова Т.И. Курс физики. М.: Высш. Шк., 2004.

КОНТРОЛЬНЫЕ ВОПРОСЫ

1. Какие колебания называются гармоническими?

2. Что называется одномерным классическим осциллятором?

3. Написать уравнение гармонических колебаний.

4. Что называется пружинным маятником? Чему равен его период?

5. Что называется математическим маятником? Чему равен его период?

6. Что называется период физического маятника? Чему равен его период?

7. Что называется приведённой длиной физического маятника?

8. Какие колебания получаются при сложении однонаправленных колебаний?

9. Какие колебания получаются при сложении взаимноперпендикулярных колебаний?

10. Написать уравнение затухающих колебаний.

11. Написать уравнение вынужденных колебаний.

12. Как происходят электрические колебания в колебательном контуре?

13. Чему равен период собственных колебаний в колебательном контуре?

14. Что такое импеданс?

15. Что называется волной?

16. Написать уравнение бегущей волны.

17. Что такое интерференция волн?

18. Что такое стоячая волна?

19. Как возникают электромагнитные волны?

20. Написать вектор Умова-Пойнтинга.

СОДЕРЖАНИЕ

ОБЩИЕ СВЕДЕНИЯ О КОЛЕБАНИЯХ. ОДНОМЕРНЫЙ КЛАССИЧЕСКИЙ

ГАРМОНИЧЕСКИЙ ОСЦИЛЛЯТОР……………………………………………… 3

Пружинный маятник…………………………………….………………… 6

Физический маятник ……………………………………………………… 7

Математический маятник ………………………………………………. 8

СЛОЖЕНИЕ КОЛЕБАНИЙ …………………………………………………………. 9

Векторная диаграмма ………………………………………………….. 9

Биения ………………………………………………………………………… 10

Сложение взаимноперпендикулярных колебаний …………. 12

ЗАТУХАЮЩИЕ КОЛЕБАНИЯ. ГАРМОНИЧЕСКИЙ ОСЦИЛЛЯТОР

ПРИ НАЛИЧИИ СИЛ СОПРОТИВЛЕНИЯ …………………………………….. 16

ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ ………………………………………………….. 20

АВТОКОЛЕБАНИЯ. ПАРАМЕТРИЧЕСКИЙ РЕЗОНАНС …………………. 27

СВОБОДНЫЕ ЭЛЕКТРИЧЕСКИЕ КОЛЕБАНИЯ В КОНТУРЕ

БЕЗ АКТИВНОГО СОПРОТИВЛЕНИЯ …………………………………………. 28

ЗАТУХАЮЩИЕ ЭЛЕКТРИЧЕСКИЕ КОЛЕБАНИЯ ………………………….. 32

ВЫНУЖДЕННЫЕ ЭЛЕКТРИЧЕСКИЕ КОЛЕБАНИЯ ………………………. 36

ПЕРЕМЕННЫЙ ТОК ………………………………………………………………… 42

УПРУГИЕ ВОЛНЫ …………………………………………………………………… 45

Уравнение упругой волны ………………………………………… 45

Принцип суперпозиции. Интерференция волн …………… 46

Стоячие волны …………………………………………………………. 47

ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ ………………………………………………. 49

ШКАЛА ЭЛЕКТРОМАГНИТНЫЪХ ВОЛН …………………………………… 53

ЛИТЕРАТУРА ………………………………………………………………………… 53

Егорова С.И., Егоров И.Н., Кунаков В.С.,

Лемешко Г.Ф., Наследников Ю.М.

КОЛЕБАНИЯ И ВОЛНЫ

Учебное пособие

Редактор О.А. Водолазова

Компьютерная обработка И.В.Кикичева

Тем план 2009, поз.

_______________________________________________________________ В печать

Объём 3,5 усл. п. л. Офсет. Формат 60х84/64.

Бумага тип №3. Заказ №43. Тираж 300. Цена «С».

Издательский центр ДГТУ

Адрес университета и полиграфического предприятия:

344000, г. Ростов-на-Дону, пл. Гагарина,1.