Гармонический осциллятор при наличии сил сопротивления

Как уже отмечалось, затухающие колебания возникают при наличии сил сопротивления (трения) и обусловлены рассеянием (диссипацией) энергии. Если убыль энергии не восполняется за счёт работы внешних сил, колебания будут затухать. В простейшем, и вместе с тем, наиболее часто встречающемся, случае сила сопротивления пропорциональна величине скорости:

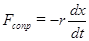, (30)

где 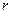- постоянная, называемая коэффициентом сопротивления. Знак минус обусловлен тем, что сила сопротивления и скорость имеют противоположные направления, следовательно, их проекции на ось 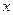имеют разные знаки.

Запишем уравнение второго закона Ньютона для движения груза на пружине при наличии сил сопротивления:

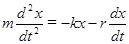. (31)

Введя обозначения: 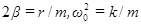, получим однородное дифференциальное уравнение затухающих колебаний:

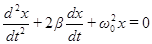, (32)

где 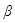- коэффициент затухания, 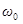- собственная частота колебаний, т.е. частота, с которой совершались бы свободные колебания системы в отсутствие сопротивления среды (при ).

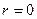Решение уравнения (32) проведем через анализ рассеяния энергии. Для этого сначала найдем полную энергию гармонического осциллятора при отсутствии сил сопротивления. Подставив в выражение для кинетической энергии скорость осциллятора (3), получим:

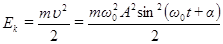. (33)

Потенциальная энергия упругой деформации после подстановки 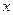из формулы (1) имеет следующий вид:

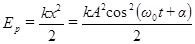. (34)

Выразив из формулы 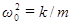коэффициент 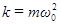и подставив его в (34), получим выражение для полной энергии гармонического осциллятора:

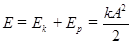. (35)

Полная энергия гармонического осциллятора сохраняется в отсутствие сил сопротивления и пропорциональна квадрату амплитуды колебаний. Таким образом, процесс колебаний связан с периодическим переходом энергии из потенциальной в кинетическую и обратно. Средние (за период колебаний) значения потенциальной и кинетической энергии одинаковы, и каждое из них равно .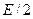

Выясним, как влияют силы сопротивления на энергию колебательной системы (осциллятора). Будем при этом считать, что сила сопротивления настолько мала, что вызываемые ею потери энергии за один период относительно малы. Потеря энергии телом определится как работа, произведённая силой сопротивления. За время 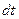эта работа, а с ней и потеря энергии 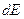равна произведению силы сопротивления 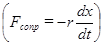на смещение тела ( ):

,

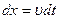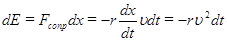откуда

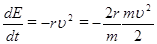. (36)

При сделанном нами предположении о малости сил сопротивления мы можем в (36) заменить кинетическую энергию половиной полной энергии осциллятора :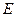

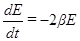. (37)

Перепишем это выражение в виде:

.

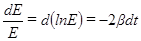Путем интегрирования находим, что 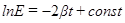, окончательно:

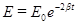, (38)

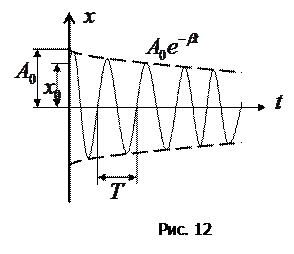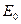где – значение энергии в начальный момент времени ( ).

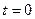Таким образом, энергия колебательной системы убывает из-за сил сопротивления по экспоненциальному закону. Вместе с энергией убывает и амплитуда колебаний. Поскольку энергия пропорциональна квадрату амплитуды, получаем

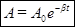. (39)

Таким образом, при не слишком большом затухании общее решение уравнения (32) имеет вид:

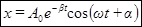. (40)

Здесь 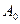– значение амплитуды в начальный момент времени, 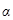- начальная фаза, 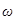- частота колебаний.

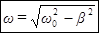. (41)

На рисунке 12 дан график функции (40). Пунктирными линиями показаны пределы, в которых находится смеще­ние 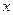колеблю­щейся точки. В соответствии с видом функции (40) движение системы можно рассматри­вать как гармони­ческое колебание частоты 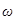с амплитудой, изменяющейся по закону, определяемому формулой (39). Верхняя из пунктирных кривых на рисунке 12 дает график функции A(t). Начальное смещение 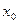зависит кроме 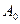также от начальной фазы :

.

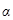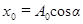Степень убывания амплитуды определяется коэффициентом затухания. За время 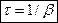амплитуда уменьшается в 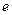раз - это время называется временем релаксации колебаний. Сделанное нами выше предположение о малости сил сопротивления означает, что 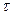предполагается большим по сравнению с периодом колебаний

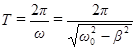, (42)

т.е. за время релаксации происходит большое число колебаний 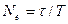. Величину, обратную N_e называют логарифмическим декрементом затухания :

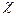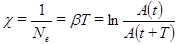. (43)

Итак, логарифмический декремент затухания обратен по величине числу колебаний, совершаемых за время релаксации. Кроме того, логарифмический декремент затухания часто определяют как натуральный логарифм отношения двух последующих амплитуд.

Для характеристики колебательной системы также вводят величину, называемую добротностью колебательной системы

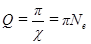. (44)

Из формулы (42) следует, что с ростом коэффициента затухания период колебаний увеличивается. При 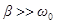движение перестаёт быть периодическим, происходит срыв колебаний, или движение носит апериодический (непериодический) характер - выведенная из положения равновесия система возвращается в положение равновесия, не совершая колебаний.

Вынужденные колебания

Пусть колебательная система, например шарик на пружине, подвергается действию внешней силы, изменяющейся со временем по гармоническому закону:

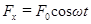. (45)

В этом случае уравнение второго закона Ньютона имеет вид:

.

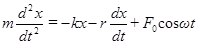Введя обозначения 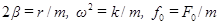, запишем это уравнение следующим образом:

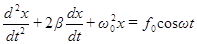. (46)

Мы получили неоднородное дифференциальное уравнение вынужденных колебаний. Общее решение неоднородного уравнения равно сумме общего решения соответствующего однородного уравнения и частного решения неоднородного уравнения. Общее решение однородного уравнения мы уже знаем (см. функцию (40), являющуюся общим решением уравнения (32)):

,

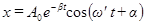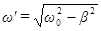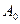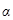где , и - произвольные постоянные.

Следует помнить, что это уравнение описывает затухающие колебания, которые представляют интерес только с точки зрения подхода к установившимся колебаниям. Нас же интересуют только установившиеся вынужденные колебания. Частное решение будем искать в виде:

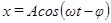. (47)

Воспользуемся помощью векторной диаграммы и метода подстановки решения (47) в исходное уравнение (46). При этом получаем:

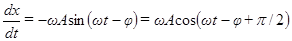; (48)

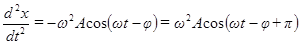. (49)

Подстановка выражений (47) - (49) в уравнение (46) приводит к соотношению:

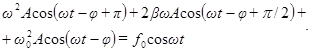(50)

Из (50) следует, что постоянные 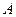и 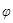должны иметь такие значения, чтобы гармоническая функция 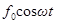была равна сумме трех гармонических функций, стоящих в левой части уравнения. Если изобразить функцию 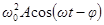вектором длиной 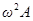, направленным вправо, то функция 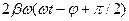изобразится вектором длиной 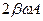(рис.13), повёрнутым относительно вектора 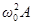против часовой стрелки на угол 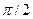, а функция 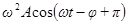- вектором длиной 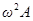, повернутым относительно вектора 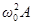на угол 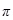. Для того, чтобы уравнение (50) было удовлетворено, сумма трех перечисленных векторов должна совпадать с вектором, изображающим функцию 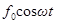. Из рисунка 13.a видно, что такое совпадение возможно лишь при значении амплитуды, которое определяется условием:

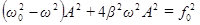, откуда

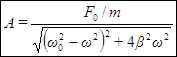. (51)

Мы заменили 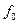отношением 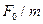. Рисунок отвечает случаю 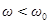. Из рисунка 13.б отвечающему случаю 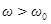получается такое же значение .

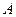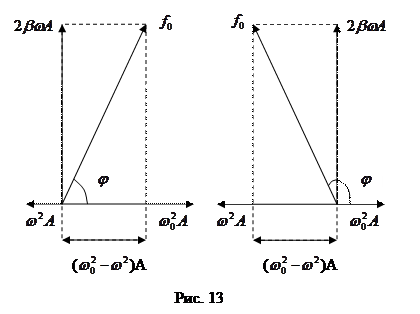
Рис. 13 позволяет получить также и значение 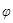, которое представляет собой величину отставания по фазе вынужденного колебания (47) от обусловившей его вынуждающей силы. Из рисунка видно, что

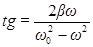. (52)

Подставив в (47) значения 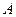из (51) и 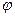из (52), получим функцию, являющуюся частным решением уравнения, описывающего установившиеся вынужденные колебания:

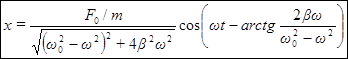. (53)

Зависимость амплитуды вынужденных колебаний от частоты вынуждающей силы приводит к тому, что при некоторой определенной для данной системы частоте амплитуда достигает максимального значения. Резкое возрастание амплитуды колебаний называется резонансом, а соответствующая частота, при которой амплитуда достигает максимального значения, называется резонансной частотой. .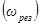

Для определения резонансной частоты нужно найти максимум функции (51) или, что то же самое, минимум выражения, стоящего под корнем в знаменателе. Продифференцировав это выражение по 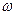и приравняв нулю, мы получим условие, определяющее резонансную частоту:

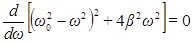
(54)

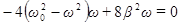
Уравнение (54) имеет три решения: 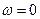и .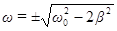

Решение, равное нулю, соответствует максимуму знаменателя. Из остальных двух решений отрицательное должно быть отброшено, как не имеющее физического смысла (частота не может быть отрицательной). Таким образом, для резонансной частоты получается одно значение.

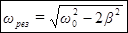(55)

Подставив это значение частоты в (51), получим выражение для амплитуды при резонансе

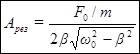(56)

Из (56) следует, что при отсутствии сопротивления среды амплитуда при резонансе обращалась бы в бесконечность. Согласно (55) резонансная частота при тех же условиях (при 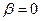) совпадает с собственной частотой колебания системы .

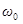Зависимость амплитуды вынужденных колебаний от частоты вынуждающей силы (или, что то же самое, от частоты колебаний) показана на рис. 14.

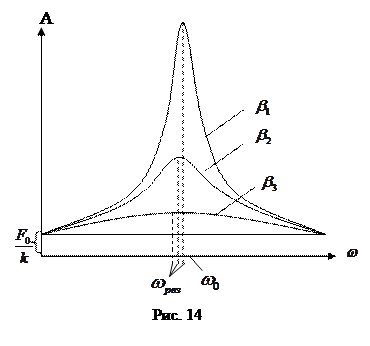
Отдельные кривые на графике соответствуют различным значениям параметра 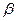. В соответствии с (55) и (56), чем меньше 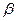, тем выше и правее лежит максимум данной кривой. При очень большом затухании (когда 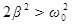) выражение для резонансной частоты становится мнимым. Это означает, что при этих условиях резонанс не наблюдается – с увеличением частоты амплитуда вынужденных колебаний монотонно убывает (см. нижнюю кривую на рис. 14). Изображенная на рис. 14 совокупность графиков функций (56), соответствующих различным значениям параметра 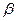, называется резонансными кривыми.

По поводу резонансных кривых можно сделать ещё следующие замечания. При стремлении 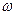к нулю все кривые приходят к одному и тому же, отличному от нуля, предельному значению, равному 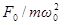, т.е. 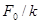. Это значение представляет собой смещение из положения равновесия, которое получает система под действием постоянной силы 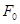. При стремлении 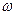к бесконечности все кривые асимптотически стремятся к нулю, так как при большой частоте сила так быстро изменяет своё направление, что система не успевает заметно сместиться из положения равновесия. Наконец, отметим, что чем меньше 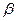, тем сильнее изменится с частотой амплитуда вблизи резонанса, тем острее получается максимум.

Из формулы (56) вытекает, что при малом затухании (т.е. при 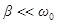) амплитуда при резонансе приближенно равна

.

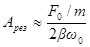Разделим это выражение на смещение 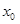от положения равновесия под действием постоянной силы 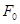, равной 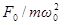. В результате получим:

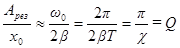(57)

Таким образом, добротность показывает, во сколько раз амплитуда в момент резонанса превышает смещение системы из положения равновесия под действием постоянной силы той же величины, что и амплитуда вынуждающей силы (это справедливо лишь при небольшом затухании).

Из рис. 13 видно, что вынужденные колебания отстают по фазе от вынуждающей силы, причем величина отставания 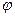лежит в пределах от 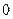до .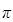

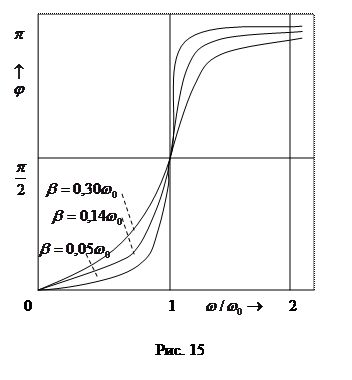
Зависимость 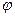от 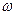при различных значениях 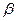показана графически на рис. 15. Частоте 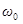соответствует 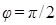. Из (55) видно, что резонансная частота меньше собственной. Следовательно, в момент резонанса 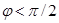. При слабом затухании 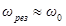и значение 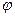при резонансе можно считать равным .

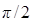С явлением резонанса приходится считаться при конструировании машин и различного рода сооружений. Собственная частота колебаний этих устройств ни в коем случае не должна быть близка к частоте возможных внешних взаимодействий. Например, собственная вибрация корпуса корабля или крыльев самолета должна сильно отличаться от частоты колебаний, которые могут быть возбуждены вращением гребного винта или пропеллера. В противном случае возникают вибрации, которые могут вызвать катастрофу. Известны случаи, когда обрушивались мосты при прохождении по ним марширующих колонн солдат. Это происходило потому, что собственная частота колебания моста была близка к частоте, с которой шагала колонна.

Вместе с тем явление резонанса часто оказывается весьма полезным, особенно в акустике, радиотехнике, и т.д.

Автоколебания.

Параметрический резонанс

Автоколебанияминазываются незатухающие колебания, обусловленные управляемым самой системой пополнением энергии от источника неколебательной природы. Любая автоколебательная система состоит из четырёх частей: колебательной системы, источника энергии неколебательной природы, клапана, регулирующего поступление энергии в колебательную систему, определенными порциями, обратной связи или устройства управления работой клапана за счет процессов в самой колебательной системе.

Обратная связь называется положительной (отрицательной), если в течение времени воздействия источника энергии на колебательную систему источник энергии производит над системой положительную (отрицательную) работу и передает ей (отнимает от нее) некоторый запас энергии. Положительная обратная связь используется для возбуждения автоколебаний. В случае отрицательной обратной связи усиливается затухание, и автоколебания подавляются.

Автоколебательными системами являются, например, часы, паровые машины и двигатели внутреннего сгорания, отбойные молотки, электрические звонки. Автоколебания совершают струны под действием смычка в скрипке, воздушные столбы в трубах духовых инструментов, язычки в баянах и аккордеонах, голосовые связки при разговоре или пении. Электрической автоколебательной системой является генератор незатухающих электрических колебаний. В ряде случаев механизм обратной связи автоколебательной системы замаскирован, и разбиение системы на основные части затруднительно.

В качестве примера автоколебательной системы рассмотрим часовой механизм. Маятник часов насажен на одну ось с изогнутым рычагом – анкером. На концах анкера имеются выступы специальной формы, называемые палеттами. Зубчатое ходовое колесо находится под воздействием цепочки с гирей или закрученной пружины, которые стремятся повернуть его по часовой стрелке. Однако большую часть времени колесо опирается на один из зубьев в боковую поверхность той или иной палетты, скользящей при качании маятника по поверхности зуба. Только в момент, когда маятник находится вблизи среднего положения, палетты перестают преграждать путь зубьям, и ходовое колесо поворачивается, толкая анкер зубом, скользящим своей вершиной по скошенному торцу палетты. За полный цикл качания маятника (период) ходовое колесо проворачивается на два зуба, причем каждый из палетт получает по толчку. Посредством этих толчков за счет энергии поднятой гири или закрученной пружины и восполняется убыль энергии маятника, возникающая вследствие трения. Итак, в часах колебательной системой является маятник. Источником энергии – поднятая вверх гиря или заведенная пружина. Клапаном является анкер. Обратная связь осуществляется взаимодействием анкера с ходовым колесом.

Существует еще один вид взаимодействия извне, с помощью которого можно сильно раскачать систему. Этот вид взаимодействия заключается в совершаемом в такт с колебаниями периодическом изменении какого-либо параметра системы, вследствие чего само явление называется параметрическим резонансом.

Возьмем для примера простейший маятник – шарик на нитке. Если периодически изменять длину маятника, увеличивая её в моменты, когда маятник находится в крайнем положении, и, уменьшая в моменты, когда маятник находится в среднем положении (рис. 16), то маятник сильно раскачается. Увеличение энергии маятника при этом происходит за счет работы, которую совершает сила, действующая на нить. Сила натяжения нити при колебаниях маятника непостоянна: она меньше в крайних положениях, когда скорость обращается в ноль, и больше в среднем положении, когда скорость маятника максимальна. Поэтому отрицательная работа внешней силы при удалении маятника оказывается меньше по величине, чем положительная работа, совершаемая при укорочении маятника. В итоге работа внешних сил за период оказывается больше нуля.