Теплота, сообщаемая системе, расходуется на изменение внутренней энергии системы и на совершение системой работы против внешних сил.

При осуществлении в системе произвольного процесса, в результате которого она вновь пришла бы в исходное состояние, изменения внутренней энергии не происходит. Математически это выражается следующим образом: 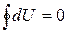. Тогда, согласно первому началу термодинамики:А = Q,то есть вечный двигатель первого рода - периодически действующий двигатель, который совершал бы работу большую, чем сообщенная ему извне энергия, невозможен.

Для работы, которая совершается при расширении или сжатии газа, заключенного в сосуд с подвижным поршнем, уравнение будет иметь следующий вид:

dА = р dV .

формула (3.4) справедлива не только для газа и жидкости, но и для твердых тел при их сжатии или растяжении под действием внешних сил, равномерно распределенных по поверхности тела.

Применение первого начала термодинамики

к изопроцессам

Изопроцессы – это процессы, при которых один из основных параметров состояния системы остается постоянным.

Изохорный (изохорический) процесс(V = const).При изохорном процессе газ не совершает работы над внешними телами, поэтому:

dА = р dV = 0.

Вся теплота, сообщаемая газу, идет на увеличение его внутренней энергии, первое начало термодинамики примет вид:

dQ = dU.

Диаграмма этого процесса – изохора в координатах р, V(рис. 3.1) изображается прямой, параллельной оси ординат.

Изобарный (изобарический) процесс(р = const). При изобарном процессе работа газа при увеличении объема от V₁ до V₂ равна

А = 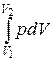= р(V₂-V₁)

и определяется площадью прямоугольника на рис. 3.2.

Тепло, переданное системе, идет на увеличение ее внутренней энергии и на совершение работы над внешними телами. Первое начало термодинамики запишется так:

dQ = dU + р dV .

Изотермический процесс (Т = const). Поскольку температура постоянна, следовательно, внутренняя энергия идеального газа не изменяется (см. стр. 16, 17). Отсюда следует, что все тепло, переданное системе, идет на совершение им работы против внешних сил. Первое начало термодинамики для изотермического процесса

dQ = dА = р dV.

Адиабатический процесс. Адиабатическим называется процесс, при котором отсутствует теплообмен(dQ = 0)между системой и окружающей средой. К таким процессам можно отнести все быстропротекающиепроцессы: быстрое сжатие или расширение газа (распространение звука в среде, двигатель внутреннего сгорания, холодильные установки).

При адиабатическом процессе первое начало записывается в виде:

dА + dU = 0,

или

dА = - dU, (3.11)
то есть внешняя работа совершается за счет убыли внутренней энергии системы.

Теплоемкость вещества

Теплоемкость удельная и молярная. Эксперименты показали, что количество тепла dQ, переданное телу или отнятое у него, пропорционально массе m тела и изменению его температуры dТ:

dQ = с m dТ,

где с – удельная теплоемкость вещества, следовательно, она выразится так:

,
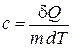то есть удельная теплоемкость вещества – величина, равная количеству теплоты, необходимой для нагревания 1 кг вещества на 1 К (Дж/кг×К).

Молярная теплоемкость вещества – величина, равная количеству теплоты, необходимому для нагревания 1 моля вещества на 1 К:

,

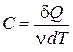где 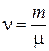–количество вещества.

Удельная теплоемкость связана с молярной теплоемкостью соотношением: С = с×m.

Различают теплоемкость при постоянном давлении С_P и теплоемкость при постоянном объеме С_V.

Первое начало термодинамики при постоянном объеме для одного моля газа:

С dТ = dU_m + р dV_m.

Если процесс изохорный, то сообщаемая газу теплота идет только на увеличение его внутренней энергии:

.

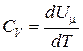Поскольку изменение внутренней энергии [см. формулу (1.14)]одного моля газа можно выразить формулой 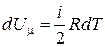, то

.

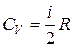Если газ нагревается при постоянном давлении, то теплоемкость моля газа

+ .

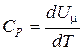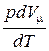Учитывая то, что внутренняя энергия газа не зависит ни от давления, ни от объема, а определяется только температурой и всегда равна С_V, продифференцировав уравнение Клапейрона-Менделеева по Т (р V_m = RТ, 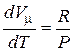), получим:

С_P = С_V +R. (3.1)

выражение (3.1) называется уравнением Майера. Оно показывает, что С_P всегда больше С_V на величину молярной газовой постоянной. Это объясняется тем, что при нагревании газа при постоянном давлении требуется еще дополнительное количество теплоты на совершение работы расширения газа, так как постоянство давления можно обеспечить только увеличением объема газа.

Это уравнение можно выразить также через число степеней свободы

.

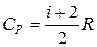При рассмотрении термодинамических процессов важно знать характерное для каждого газа соотношение С_P к С_V:

.

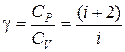Из этих формул следует, что молярные теплоемкости определяются лишь числом степеней свободы и не зависят от температуры. Однако это утверждение справедливо в широком интервале температур только для одноатомных газов. Для двухатомных молекул теплоемкость зависит от температуры. Так из качественной экспериментальной зависимости молярной теплоемкости водорода вытекает, что С_V следующим образом зависит от температуры (рис. 3.3).

Такую зависимость можно объяснить тем, что при низких температурах наблюдается только поступательное движение молекул газа. При комнатных – добавляется вращение, а при очень высоких – к этим двум видам движения добавляются еще и колебательные движения молекул.

Уравнение Пуассона. Политропный процесс

Рассмотрим уравнение, связывающее параметры газа при адиабатическом процессе. Поскольку при адиабатическом процессе dQ = 0, то первое начало термодинамики для одного моля газа примет вид:

С_V dТ + р dV ₀= 0. (3.2)

Напишем уравнение Клапейрона-Менделеева:рV₀ = RТ, выразим отсюда давление: р = RТ / V₀,и подставимего в уравнение (3.2):

.

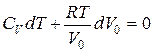Учитывая, что R = С_P - С_V[см. (3.1)], получим:

.

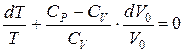Так как 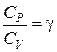[см. (3.22)], то последнее равенство можно записать в виде:

.

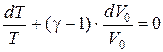Проинтегрировав это выражение, получим:

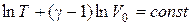
или .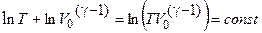

Поскольку величина, логарифм которой постоянен, тоже постоянная, то:

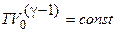. (3.3)

выражение (3.3) является уравнением адиабатического процесса,также ононазывается уравнением Пуассона.

Для перехода к другим переменным, например р и Т или р и V₀, исключим из уравнения (3.3) температуру или объем с помощью уравнения Клапейрона-Менделеева (1.8), получим соответственно:

,

.

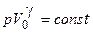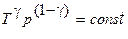В этих уравнениях безразмерная величина g называется показателем адиабаты, адиабатической постоянной или коэффициентом Пуассона. Диаграмма адиабатического процесса (адиабата) в координатах давления и объема изображена на рис. 3.4

Адиабата 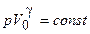,падает круче, чем изотерма 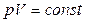.Это объясняется тем, что при адиабатическом сжатии 1 - 3 увеличение давления газа обусловлено не только уменьшением его объема, как при изотермическом процессе, но и повышением температуры.

Все рассмотренные выше процессы: изохорный, изобарный, , изотермический, адиабатический имеют одну общую особенность – каждый из них происходит при постоянной теплоемкости. Изохорный - приС_V, изобарный – при С_P, при изотермическом процессе теплоемкость равна ±¥, а в адиабатическом теплоемкость равна нулю.

Процесс, в котором теплоемкость остается постоянной, называется политропным. Исходя из первого начала термодинамики[см. (3.1), (3.2), (3,3)] при условии постоянства теплоемкости (C = const) можно вывести уравнение политропы:

,

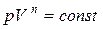где 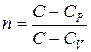– безразмерная постоянная величина называется показателем политропы. Четырем процессам, о которых говорилось выше, соответствуют различные значения показателя политропы.

Например, при: n=0 получим изобарный процесс (р = const);

n = 1 – изотермический процесс(pV = const);

n =± ¥ - изохорный процесс (V = const);

n =g - адиабатный процесс (С = 0).

Работа газа при изопроцессах

Изохорный процесс [см. формулу (1.5)]. При этом процессе работа газа равна нулю, поскольку V = const,тоdА = 0.

Изобарный процесс [см. формулу (1.4)]. При изменении объема газа от V₁ до V₂ совершается работа

А = 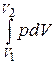= р (V₂ -V₁).

Если использовать уравнение Клапейрона-Менделеева для выбранных нами двух состояний, то

; ,

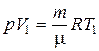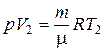откуда ,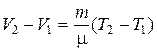

тогда выражение для работы изобарного расширения примет вид:

.

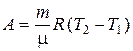Из этого выражения вытекает физический смысл молярной газовой постоянной: если разность температур равна 1 К, то для 1 моля газа R=A, то есть газовая постоянная Rчисленно равнаработе изобарного расширения 1 моля идеального газа при нагревании его на 1 К.

Изотермический процесс. Изотермический процесс описывается законом Бойля-Мариотта[см. формулу (1.1)].При изотермическом расширении газа работа равна:

А= = .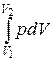

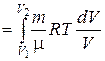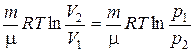Это и есть работа газа против внешних сил, причем вся теплота, сообщаемая газу, расходуется на совершение работы.

Адиабатический процесс. При адиабатическом процессе работа совершается за счет внутренней энергии. Если газ адиабатически расширяется от V₁ до V₂, то его температура уменьшается от Т₁ до Т₂.

Тогда выражение для работы расширения идеального газа можно записать в таком виде:

.

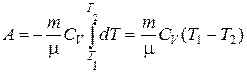Для того, чтобы перейти к другой переменной V,воспользуемся уравнением Клапейрона-Менделеева, а также тем, что

С_V = .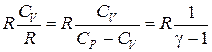

В результате получим выражение для работы при адиабатическом процессе для любой массы газа:

.

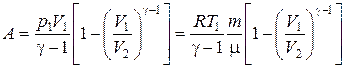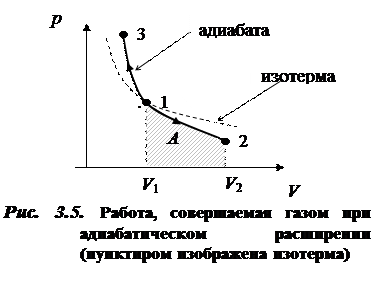Работа, совершаемая газом при адиабатическом расширении 1 ® 2, определяется площадью под кривой от точки 1 до точки 2 (рис. 3.5).

Видно, что работа, которая совершается при адиабатическом процессе меньше, чем при изотермическом. Это объясняется тем, что при адиабатическом расширении происходит охлаждение газа, тогда как при изотермическом – температура поддерживается постоянной за счет притока извне эквивалентного количества теплоты.

Обратимые и необратимые процессы. Циклы

Для описания термодинамических процессов одного первого начала термодинамики, которое устанавливает связь между теплотой, работой и изменением внутренней энергии, недостаточно, поскольку первое начало термодинамики не определяет направление тепловых процессов, а только выражает закон сохранения и превращения энергии. Ограниченность первого начала термодинамики привела к необходимости расширения теоретических основ термодинамики. Но для того, чтобы перейти к обсуждению сути и формулировки второго начала термодинамики, расширим свои представления о термодинамических процессах, в частности, познакомимся с циклами (круговыми процессами),обратимымиинеобратимымипроцессами, а также с понятием энтропии.

Круговым процессом или циклом называется процесс, при котором система, пройдя через ряд состояний, возвращается в исходное (рис. 3.6). На диаграмме процессов цикл изображается замкнутой кривой. Цикл, совершаемый идеальным газом, можно разбить на процессы расширения (1®2) и сжатия (2®1). Работа расширения газа положительна (dV > 0, площадь 1а2V₂V₁1), работа сжатия – отрицательна (dV < 0, площадь 2б1V₁V₂ 2).

Работа, совершаемая газом за цикл, определяется площадью, охватываемой замкнутой кривой. Если цикл протекает по часовой стрелке, то он называется прямым (совершается положительная работа). Если цикл протекает против часовой стрелки, то совершается отрицательная работа, цикл называется обратным.

Прямой цикл используется в тепловых двигателях (в теплоотдатчиках), а обратный - в холодильных установках (в теплоприемниках).

В результате кругового процесса система возвращается в исходное состояние, следовательно, полное изменение внутренней энергии газа равно нулю. Поэтому первое начало термодинамики для кругового процесса

Q = DU + А = А.

Работа, совершаемая за цикл, равна количеству полученной извне теплоты. Однако система может и отдавать теплоту, поэтому

Q = Q₁ - Q₂,

где Q₁ – количество теплоты, полученное системой,Q₂ - количество теплоты, отданное системой. Термический коэффициент полезного действия (к.п.д.) для кругового процесса выражается следующим образом:

.

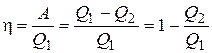Из определения кпд следует, что он не может быть больше единицы. например, кпд паровой турбины – 0,2; дизеля – 0,35.

Термодинамический процесс называется обратимым, если он может происходить как в прямом, так и в обратном направлении. Причем, если такой процесс происходит сначала в прямом, а затем в обратном направлении, то в окружающей среде и в самой системе не происходит никаких изменений.

Любой другой процесс, который не удовлетворяет этим условиям, называется необратимым. Всякий обратимый процесс является равновесным.

Примером обратимого процесса (до некоторой степени) могут служить незатухающие колебания, которые совершает в вакууме тело, подвешенное на абсолютно упругой пружине: изменения состояния системы связано только с изменением ее конфигурации и скорости движения, при этом механические колебания не вызывают теплового движения частиц. Примером необратимого процесса в механике является торможение тела под действием силы трения: энергия механического движения тела уменьшается и расходуется на увеличение теплового движения частиц самого тела и окружающей среды.

Примерами необратимых процессов в молекулярной физике могут служить расширение газа в пустоту и переход теплоты от более нагретого тела к менее нагретому. Однако надо всегда помнить, что обратимые процессы – это идеализация. Реальные процессы всегда сопровождаются диссипацией энергии. Но изучение обратимых процессов важно, поскольку обратимые процессы являются наиболее экономичными.

Второе начало термодинамики

Существует несколько формулировок второго начала термодинамики, две из которых приведены ниже:

· теплота сама собой не может переходить от тела с меньшей температурой к телу с большей температурой (формулировка Р. Клаузиуса);

· невозможен вечный двигатель второго рода, то есть такой периодический процесс, единственным результатом которого было бы превращение теплоты в работу вследствие охлаждения одного тела (формулировка Томсона).

Второй закон термодинамики указывает на неравноценность двух форм передачи энергии – работы и теплоты. Этот закон учитывает тот факт, что процесс перехода энергии упорядоченного движения тела как целого (механической энергии) в энергию неупорядоченного движения его частиц (тепловую энергию) необратим. Например, механическая энергия при трении переходит в теплоту без каких-либо дополнительных процессов. Переход же энергии неупорядоченного движения частиц (внутренней энергии) в работу возможен лишь при условии, что он сопровождается каким-либо дополнительным процессом. Так, тепловая машина, работающая по прямому циклу, производит работу только за счет подводимой от нагревателя теплоты, но при этом часть полученной теплоты передается холодильнику.

Энтропия.Кроме внутренней энергииU, которая является однозначной функцией параметров состояния системы, в термодинамике широко используются и другие функции состояния (свободная энергия, энтальпия и энтропия).

Понятие энтропии введено в 1865 году Рудольфом Клаузиусом. Это слово происходит от греч. entropia и в буквальном смысле означает поворот, превращение. в термодинамике этим термином пользуются при описании превращений различных видов энергии (механической, электрической, световой, химической) в тепловую, то есть в беспорядочное, хаотическое движение молекул. Собрать эту энергию и превратить ее снова в те виды, из которых она была получена, невозможно.

Для определения меры необратимого рассеяния или диссипации энергии и было введено это понятие. Энтропия S является функцией состояния. Она выделяется среди других термодинамических функций тем, что имеет статистическую, то есть вероятностную природу.

Если в термодинамической системе происходит процесс, связанный с получением или отдачей теплоты, то это ведет к превращению энтропии системы, которая может и возрастать, и убывать. В ходе необратимого цикла энтропия изолированной системы возрастает

dS > 0. (3.4)

Это означает, что в системе происходит необратимое рассеяние энергии.

Если в замкнутой системе происходит обратимый процесс, энтропия остается неизменной

dS = 0. (3.5)

Изменение энтропии изолированной системы, которой сообщено бесконечно малое количество тепла, определяется соотношением:

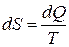. (3.6)

Это соотношение справедливо для обратимого процесса. Для необратимого процесса, происходящего в замкнутой системе, имеем:

dS > .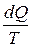

В незамкнутой системе энтропия всегда возрастает. Функция состояния, дифференциалом которой является 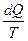, называется приведенной теплотой.

Таким образом, во всех процессах, происходящих в замкнутой системе, энтропия возрастает при необратимых процессах и остается неизменной при обратимых процессах. Следовательно, формулы (3.4) и (3.5)можно объединить и представить в виде

dS ³ 0.

Это статистическая формулировка второго начала термодинамики.

Если система совершает равновесный переход из состояния 1 в состояние 2, то согласно уравнению (3.6) , изменение энтропии

DS_1-2 = S₂ – S₁= .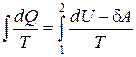

Физический смысл имеет не сама энтропия, а разность энтропий.

Найдем изменение энтропии в процессах идеального газа. Поскольку:

; ;

,

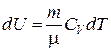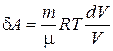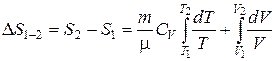или: 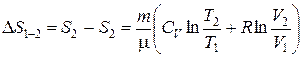. (3.7)

Отсюда видно, что изменение энтропии идеального газа при переходе из состояния 1 в состояние 2 не зависит от вида процесса перехода 1® 2.

Из формулы (3.7) следует, что при изотермическом процессе (Т₁ = Т₂):

.

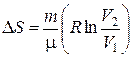При изохорном процессе изменение энтропии равно

.

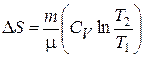Так как для адиабатического процессаdQ = 0, то иDS = 0, следовательно, обратимый адиабатический процесс протекает при постоянной энтропии. Поэтому его называют изоэнтропийным процессом.

Энтропия системы обладает свойством аддитивности, это означает, что энтропия системы равна сумме энтропий всех тел, которые входят в систему.

Смысл энтропии становится более понятным, если привлечь статистическую физику. В ней энтропия связывается с термодинамической вероятностью состояния системы. Термодинамическая вероятность W состояния системы равна числу всевозможных микрораспределений частиц по координатам и скоростям, которое обусловливает данное макросостояние: Wвсегда³ 1,то есть термодинамическая вероятность не есть вероятность в математическом смысле.

Л. Больцман (1872 г.) показал, что энтропия системы равна произведению постоянной Больцмана k на логарифм термодинамической вероятности W данного состояния

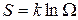(3.8)

Следовательно, энтропии можно дать следующее статистическое толкование: энтропия есть мера неупорядоченности системы. Из формулы (3.8) видно: чем больше число микросостояний, реализующих данное макросостояние, тем больше энтропия. Наиболее вероятное состояние системы – это равновесное состояние. Число микросостояний при этом максимально, следовательно, максимальна и энтропия.

Поскольку все реальные процессы необратимы, то можно утверждать, что все процессы в замкнутой системе ведут к увеличению энтропии – принцип возрастания энтропии.

При статистическом толковании энтропии это означает, что процессы в замкнутой системе идут в направлении от менее вероятных состояний к более вероятным состояниям до тех пор, пока вероятность состояний не станет максимальной.

Поясним на примере. Представим себе сосуд, разделенный перегородкой на две равные части А и Б. В части А находится газ, а в Б - вакуум. Если сделать отверстие в перегородке, то газ немедленно начнет «сам собою» расширяться и через некоторое время равномерно распределится по всему объему сосуда и это будет наиболее вероятное состояние системы. Наименее вероятным будет состояние, когда большая часть молекул газа вдруг самопроизвольно заполнит одну из половинок сосуда. Этого явления можно ждать сколь угодно долго, однако газ сам по себе не соберется вновь в части А. Для этого нужно совершить над газом некоторую работу: например, как поршень передвинуть правую стенку части Б. Таким образом, любая физическая система стремится перейти из состояния менее вероятного в состояние более вероятное. Равновесное состояние системы – более вероятное.

Используя понятие энтропии и неравенство Р. Клаузиуса, второе начало термодинамикиможно сформулировать какзакон возрастания энтропии замкнутой системы при необратимых процессах:

любой необратимый процесс в замкнутой системе происходит так, что система с большей вероятностью переходит в состояние с большей энтропией, достигая максимума в состоянии равновесия.Или иначе:

в процессах, происходящих в замкнутых системах, энтропия не убывает.

Следует обратить внимание на то, что речь идет только о замкнутых системах.

Итак, второй закон термодинамики является статистическим законом. Он выражает необходимые закономерности хаотического движения большого числа частиц, входящих в состав изолированной системы. Однако статистические методы применимы лишь в случае огромного количества частиц в системе. Для малого количества частиц (5-10) этот подход неприменим. В этом случае вероятность пребывания всех частиц в одной половине объема уже не равна нулю или другими словами - такое событие может реализоваться.

Тепловая смерть Вселенной. Р. Клаузиус, рассматривая Вселенную, как замкнутую систему, и, применяя к ней второе начало термодинамики, свел все к утверждению, что энтропия Вселенной должна достигнуть своего максимума. Это означает, что все формы движения должны перейти в тепловую, в результате чего температура всех тел во Вселенной со временем сравняется, наступит полное тепловое равновесие, и все процессы просто прекратятся: наступит тепловая смерть Вселенной.

Основное уравнение термодинамики. Это уравнение объединяет формулы первого и второго начала термодинамики:

dQ = dU + р dV, (3.9)

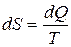. (3.10)

Подставимуравнение (3.9), выражающее второе начало термодинамики, в равенство (3.10):

.

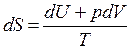Это и есть основное уравнение термодинамики.

В заключение еще раз отметим, что если первый закон термодинамики содержит энергетический баланс процесса, то второй закон показывает его возможное направление.

Третье начало термодинамики

Ещё один закон термодинамики был установлен в процессе исследования изменения энтропии химических реакций в 1906 г. В. Нернстом. Он носит название теорема Нернста или третье начало термодинамики и связан с поведением теплоемкости веществ при абсолютном нуле температур.

Теорема Нернста утверждает, что при приближении к абсолютному нулю энтропия системы также стремится к нулю, независимо от того, какие значения принимают все остальные параметры состояния системы:

.

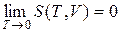Поскольку энтропия 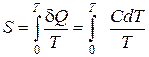, а температура Т стремится к нулю, теплоемкость вещества также должна стремиться к нулю, причем быстрее, чем Т. Отсюда следует недостижимость абсолютного нуля температуры при конечной последовательности термодинамических процессов, то есть конечного числа операций – циклов работы холодильной машины (вторая формулировка третьего начала термодинамики).

Реальные газы

Уравнение Ван-дер-Ваальса

Изменение состояния разреженных газов при достаточно высоких температурах и низких давлениях описывается законами идеального газа. Однако при увеличении давления и понижении температуры реального газа наблюдаются значительные отступления от этих законов, обусловленные существенными различиями между поведением реальных газов и поведением, которое приписывается частицам идеального газа.

Уравнение состояния реальных газов должно учитывать:

· конечное значение собственного объема молекул;

· взаимное притяжение молекул друг к другу.

Для этого Я. Ван-дер-Ваальс предложил включить в уравнение состояния не объем сосуда, как в уравнении Клапейрона-Менделеева (pV = RT), а объем моля газа, не занятый молекулами, то есть величину (V_m - b), где V_m – молярный объем. Для учета сил притяжения между молекулами Я. Ван-дер-Ваальс ввел поправку к давлению, входящему в уравнение состояния.

Внося поправки, связанные с учетом собственного объема молекул (сил отталкивания) и сил притяжения в уравнение Клапейрона-Менделеева, получим уравнение состояния моля реального газа в виде:

.

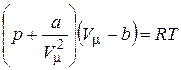Это уравнение Ван-дер-Ваальса, в котором постоянные а и b имеют разное значение для разных газов.

Лабораторная работа 9