Методы регистрации радиоактивного излучения

Эти методы основаны на исследовании тех следов, которые оставляют частицы при прохождении через вещество.

Заряженные частицы производят ионизацию молекул. Нейтральные могут быть обнаружены в момент распада на заряженные частицы или в момент соударения с ядром.

Приборы делятся на два класса:

1) приборы, которые регистрируют сам факт пролёта частицы и в некоторых случаях позволяют судить об энергии частицы (сцинтилляционный счётчик, счётчик Гейгера-Мюллера, черенковский счётчик и т.д.)

2) приборы, позволяющие наблюдать и фотографировать следы (треки), оставляемые частицей при прохождении через вещество (камера Вильсона, диффузионная камера, пузырьковая камера и т.д.)

Рассмотрим примеры счётчиков, относящихся к разным классам.

1. Счетчик Гейгера-Мюллера.

Счетчик Гейгера представляет собой тонкостенную металлическую трубку, по оси которой натянута проводящая нить (см. рис. 18). Между стенкой трубки и центральной нитью приложено напряжение порядка тысячи вольт. В трубке находится газ под пониженным давлением (100 ‑ 200 мм рт. ст). Ионизирующая частица проникает через поверхность трубки и вызывает ионизацию газа. Электроны под действием поля движутся к центральной нити. Поскольку нить малого диаметра, напряженность электри­ческого поля у ее поверхности очень велика, поэтому возникает коронный разряд, быстро распространяющийся по всей длине нити. В результате возникает импульс тока, который регистрируется соответствующим устройством.

Для счета 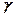-квантов трубку делают стеклянной, а внутреннюю поверхность покрывают тонким слоем металла.

Для счета 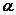-частиц трубку делают толстостенной, а торец покрывают тончайшей фольгой.

2. Камера Вильсона.

Камера Вильсона представляет собой цилиндр с поршнем (см. рис. 19). При резком опускании поршня происходит адиабатическое расширение и охлаждение газа. Пары жидкости переходят в пересыщенное состояние и легко конденсируются на ионах. Таким образом, если в этот момент через камеру пролетает частица, на ее пути образуются ионы, на которых конденсируются пары жидкости. По характеру следа можно определить тип частицы.

Если поместить камеру Вильсона в магнитное поле, то по искривлению траектории можно судить о знаке заряда, а если известны масса и заряд частицы, то по радиусу кривизны можно определить энергию частицы и т.д.

Ядерные реакции

Ядерной реакцией называется процесс взаимодействия ядра с элементарной частицей или с другим ядром, приводящий к преобразованию ядра. При этом взаимодействующие частицы должны сблизиться до расстояний порядка .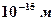

Ядерные реакции символически записывают в виде:

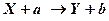
В качестве частиц 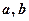могут быть нейтрон 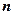, протон 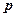, ядро тяжелого водорода 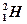- дейтрон, 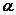-частицы, 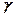-кванты. При этом реакции идут как с выделением, так и с поглощением тепла.

Реакции с медленными частицами

Реакции с медленными частицами идут по схеме:

.

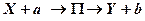Здесь 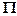‑ компаунд-ядро ‑ возбужденное ядро 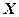, поглотившее частицу .

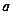Если 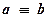, то такой процесс называют рассеянием частицы на ядре 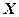. Если при этом энергии частиц равны, т.е. 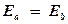, то такое рассеяние называется упругим рассеянием. Если же 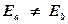, то такое рассеяние называется неупругим рассеянием.

Но рассеяние ‑ не ядерная реакция. Ядерная реакция будет тогда, когда частица 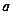не тождественна частице .

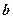Реакции с быстрыми нейтронами

Реакции с быстрыми нейтронами или дейтронами происходят без образования промежуточного ядра. Наибольшее значение имеют реакции, вызываемые нейтронами, т.к. нейтроны не имеют заряда и, следовательно, они могут обладать меньшей энергией. Но если меньше энергия нейтрона, то меньше и его скорость пролета вблизи ядра. Но при этом, соответственно, больше время нахождения нейтрона около ядра и, следовательно, больше вероятность захвата нейтрона ядром.

Следовательно, чем меньше энергия нейтрона, тем больше вероятность ядерной реакции. При определенной энергии нейтрона имеет место резонансное его поглощение. В частности, для ядра 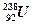эта резонансная энергия нейтрона равна .

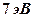Здесь имеет место процесс, аналогичный поглощению фотонов. Если энергия фотона соответствует разности энергий разрешенных уровней, то происходит интенсивное поглощение фотонов данной энергии.

Ядро также обладает разрешенными энергетическими уровнями и, следовательно, энергия нейтрона 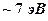соответствует разности уровней возбужденного ядра.

Деление тяжелых ядер

В 1938 г. немецкие физики О.Ган и Ф.Штрассман обнаружили, что при облучении урана нейтронами происходит деление ядер и образуются элементы из середины периодической таблицы Меделеева. Причем уран 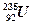делится на осколки, массы которых относятся как .

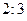Энергия связи, приходящаяся на один нуклон, больше для средних ядер, чем для тяжелых. Поэтому данная реакция должна идти с выделением энергии.

Но самым важным оказалось то, что при делении освобождаются еще несколько нейтронов. Дело в том, что, как уже отмечалось, у тяжелых ядер относительное число нейтронов больше, чем у средних ядер. Следовательно, осколки ядра переобогащены нейтронами, поэтому осколки испытывают ядерные превращения, испуская нейтроны, которые в свою очередь вызывают деление новых ядер 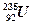. В среднем, на каждый акт деления приходится 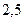выделившихся нейтронов.

Кроме 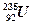при облучении нейтронами делятся плутоний ‑ 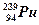, торий ‑ 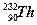и другие элементы.

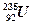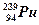Ядра и делятся нейтронами любых энергий, но особенно хорошо медленными или тепловыми энергией не меньше 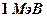. При меньших энергиях происходит просто захват нейтрона.

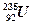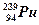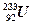Возникающие при делении ядер , и нейтроны делают возможным осуществление цепной реакции.

Пусть произошло деление только одного ядра. При этом вылетело 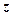нейтронов. Эти 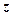нейтронов вызвали деление 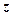ядер. При этом будет испущено 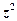нейтронов. Они вызовут деление 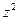ядер, которые испустят 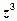нейтронов и т.д. Получается геометрическая прогрессия.

Но это ‑ идеальный случай. В реальной ситуации часть нейтронов покинет зону реакции прежде, чем будут захвачены каким-либо ядром и вызовут его деление. Часть нейтронов поглотится ядрами неделящихся примесей, и выйдут из игры.

Если даже взять чистый уран 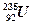, очищенный от 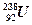(в природной руде урана 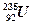содержится 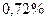, а 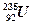‑ 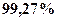), то и здесь необходима некоторая критическая масса, чтобы пошла реакция деления.

По расчетам для 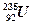критическая масса составляет около 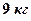. Критические размеры ‑ шар, диаметром около .

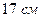Ядерное оружие и ядерная энергетика

Таким образом, если масса урана 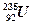превысит критическую массу, то начнется цепная реакция с выделением большого количества энергии. Это обстоятельство используют для создания атомной бомбы (см. рис. 20).

Две полукритические массы 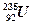или 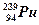находятся на безопасном расстоянии друг от друга. Прочность оболочки рассчитана на взрыв обычной бомбы и не разрушается при этом. При взрыве обычной бомбы происходит очень быстрое сближение полукритических масс 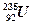, их результирующая масса превышает критическую и начинается цепная реакция.

Высвобождается огромная энергия при цепной реакции деления. Температура продуктов взрыва превышает миллион градусов. Весь заряд мгновенно испаряется, и большая часть ядерного горючего разлетается в стороны, не претерпев деления.

В природной руде урана, как мы отмечали, существует преобладание изотопа 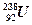( 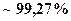) над изотопом 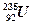, которого в руде всего 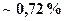. Поэтому в природном уране реакция деления не идет.

Первые атомные котлы начали строить в США приблизительно в 1942 – 1944 годах. Атомный котел служит для получения ядерного горючего - плутония. Дело в том, что экономически выгоднее получать плутоний для использования в плутониевых бомбах, чем производить химическое разделение изотопов 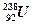и 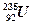. Первую атомную бомбу взорвали США в 1945 г.

Затем появились исследовательские реакторы для получения потока быстрых нейтронов. И только затем появились энергетические атомные реакторы, служащие, например, для получения электрической энергии.

Первая атомная электростанция в СССР была пущена в 1954 г. Потом появились мобильные атомные электростанции, атомные двигатели на транспорте (атомные ледоколы). Позже появились атомные электростанции, непосредственно преобразующие атомную энергию в электрическую, путем использования полупроводников.

Кроме того, необходимо отметить применение так называемых «меченых атомов» в технике, в сельском хозяйстве, медицине и т.д.

Термоядерные реакции

Как мы уже отмечали, энергетически возможны ядерные реакции синтеза легких ядер. Но для этого необходимо преодолеть силы кулоновского отталкивания, чтобы сблизить ядра на расстояния радиуса действия ядерных сил. Необходимая для этого энергия должна иметь величину:

.

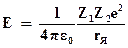Оценим порядок необходимой энергии для случая :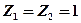

.

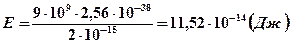Оценим теперь температуру, при которой могут быть достигнуты такие энергии, учитывая, что 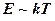( 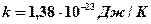- постоянная Больцмана) и на долю каждого сталкивающегося ядра приходится энергия :

.

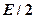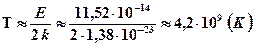Видим, что для сближения ядер на такие расстояния необходима температура порядка нескольких миллиардов градусов. Такие температуры реализуются в частности в звездах. При этом там идут реакции выгорания водорода и образования гелия. Эта реакция идет в три этапа.

На первом этапе идет реакция слияния водорода с образованием дейтерия, позитрона и нейтрино:

.

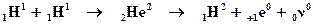На втором этапе идет реакция синтеза водорода и дейтерия с образованием изотопа гелия и 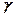-квантов:

.

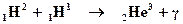На третьем этапе идет реакция синтеза изотопов гелия с образованием гелия и водорода:

.

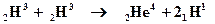Кроме того, возможны реакции с участием ядер катализаторов.

Водородная бомба

Расчеты показывают, что легче всего идет реакция:

.

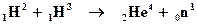Но для этого, как отмечалось, необходима очень высокая температура. Поэтому вначале в очень прочной оболочке взрывают атомную бомбу, при этом развиваются необходимые температуры и начинает идти реакция неуправляемого ядерного синтеза ‑ термоядерный взрыв.

Управляемые термоядерные реакции

Для реакции синтеза легких ядер необходимо создать и поддерживать в некотором объёме температуру порядка 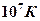. Однако следует учесть, что при данной температуре существуют частицы, скорость которых больше средней скорости частиц при данной температуре. Поэтому условия для ядерного синтеза могут реализоваться и при более низких температурах.

В 1964 году удалось получить плазму, температура которой порядка нескольких десятков миллионов. Однако для управляемого термоядерного синтеза предстоит решить еще очень много проблем. Например, где, в какой емкости должна идти эта реакция. Ведь при температуре в несколько миллионов градусов стенки реактора мгновенно превратятся в пар. Существуют также и другие проблемы.

1. Элементы квантовой механики

Гипотеза Луи де Бройля

Французский физик Луи де Бройль в 1924 году выдвинул гипотезу об универсальности корпускулярно-волнового дуализма. Де Бройль утверждал, что не только фотоны, но и электроны и любые элементарные частицы наряду с корпускулярными обладают также волновыми свойствами.

По де Бройлю с каждым микрообъектом связываются характеристики: корпускулярные – энергия 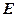и импульс 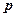; волновые – частота и длина волны . Однако, электроны и большинство других элементарных частиц имеют массу покоя, а фотоны «в покое» не существуют.

Любой микрочастице, обладающей импульсом 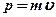, сопоставляют волну, длина которой вычисляется по формуле де Бройля. Длина волны де Бройля:

,

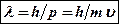где 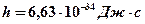– постоянная Планка, 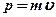– импульс частицы.

Гипотеза де Бройля была подтверждена экспериментально.

В 1927 г. американские физики Девиссон и Джермер обнаружили, что пучок электронов, рассеивающийся от естественной дифракционной решетки (кристалле никеля) дает отчетливую дифракционную картину, аналогичную той, которая имеет место от рентгеновских лучей. Дифракционные максимумы соответствовали формуле Вульфа – Брэгга, а длина волны оказалась равной длине волны, вычисленной по де Бройлю.

Советский ученый Тартаковский наблюдал дифракционную картину при прохождении пучка быстрых электронов через металлическую фольгу.

Штерн и его сотрудники показали, что дифракционные явления обнаруживаются также у атомных, молекулярных и нейтронных пучков.

Таким образом, микрочастицы обладают волновыми свойствами.

Соотношение неопределенностей

В классической механике всякая частица движется по определенной траектории, так что в любой момент времени точно фиксированы ее координата и импульс. Микрочастицы в виду наличия у них волновых свойств не имеют траектории, и неправомерно говорить об одновременных точных значениях ее координаты и импульса.

В. Гейзенберг, учитывая волновые свойства микрочастиц, пришел в 1927 году к выводу, что объект микромира невозможно одновременно с одинаковой степенью точности характеризовать его координатой и импульсом.

Согласно соотношению неопределенностей Гейзенберга, микрочастица не может иметь одновременно определенные координату ( 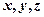), и соответствующую проекцию импульса ( 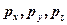), причем неопределенности в значениях этих величин удовлетворяют условиям

,

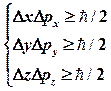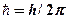
где 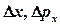, , 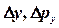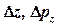- соответственно неопределенности координат и импульсов.

В квантовой теории рассматривается соотношение неопределенностей для энергии 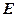и времени 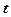, т.е. неопределенности в значениях этих величин удовлетворяют условию

.

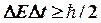Следовательно, система, имеющая среднее время жизни 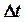, не может быть охарактеризована определенным значением энергии. Разброс значений энергии 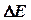возрастает с уменьшением среднего времени жизни.

Так как в классической механике принимается, что измерение координаты и импульса может быть произведено с любой точностью, то соотношение неопределенностей является квантовым ограничением применимости классической механики к микрообъектам.

Волновая функция и ее статистический смысл

Квантовая механика описывает законы движения и взаимодействия микрочастиц с учетом их волновых свойств.

Согласно волновым представлениям о природе света, интенсивность дифракционной картины пропорциональна квадрату амплитуды световой волны. С точки зрения корпускулярной теории интенсивность определяется числом фотонов, попадающих в данную точку дифракционной картины. Следовательно, дифракционная картина для микрочастиц является проявлением статистической (вероятностной) закономерности, согласно которой частицы попадают в те места, где интенсивность волн де Бройля наибольшая.

В квантовой механике состояние микрочастицы описывается волновой функцией 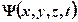. Квадрат модуля волновой функции 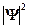определяет вероятность 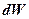нахождения частицы в момент времени 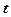в элементе объема 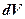. 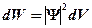, отсюда 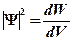- имеет смысл плотности вероятности.

Вероятность найти частицу в момент времени 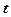в конечном объеме 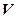равна .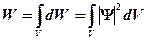

Если объем равен бесконечности, т.е. частица находится где-то в пространстве, то выполняется условие нормировки вероятности:

,

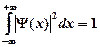
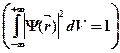где 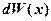– вероятность того, что частица может быть обнаружена вблизи точки с координатой 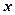на участке 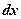, 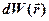- вероятность обнаружения микрочастицы в объёме .

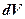Свойства волновой функции:

Функция 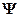, характеризует вероятность обнаружения микрочастицы в элементе объема, поэтому должна быть конечной .

Функция 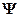должна быть однозначной, так как вероятность не может быть неоднозначной величиной.

Функция 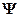должна быть непрерывной, так как вероятность не может изменяться скачком.

Функция 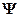удовлетворяет принципу суперпозиции (если система может находиться в различных состояниях, описываемых волновыми функциями 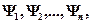то она также может находиться в состоянии 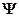, описываемом линейной комбинацией этих функций: ).

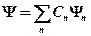Уравнение Шредингера

Микрочастицы обладают волновыми свойствами, поэтому классическая механика не может дать правильного описания их поведения. Квантовая механика создана Э.Шредингером, В.Гайзенбергом, П.Дираком и другими учеными. Основное уравнение нерелятивистской квантовой механики в 1926 году сформулировано Э. Шредингером.

Нестационарное (общее) уравнение Шредингера:

,

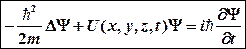где 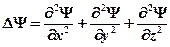- оператор Лапласа (записан в декартовых координатах), 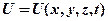- потенциальная энергия частицы в силовом поле, 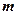– масса микрочастицы, 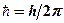, 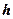– постоянная Планка, 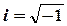- мнимая единица. Уравнение справедливо для любой частицы, движущейся с малой (по сравнению со скоростью света) скоростью.

Рассмотрим свободно движущуюся частицу, которой, согласно идее де Бройля, сопоставляется плоская волна. Уравнение плоской волны, распространяющейся вдоль оси 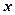, имеет вид:

.

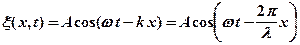Это выражение в комплексном виде: ,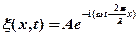

где 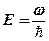- полная энергия частицы; 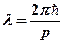- длина волны, 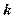- волновое число.

Получим для одномерного случая свободно движущейся частицы волновую функцию

.

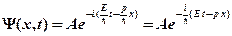Зависимость энергии от импульса: 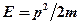. (26)

Дифференцируя функцию 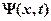один раз по 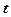и дважды по 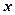, получим:

; .

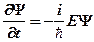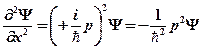Из этих соотношений найдем 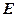и 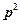через функцию 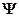и ее производную:

, .

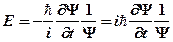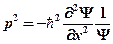Подставляя эти выражения в (26), получим дифференциальное уравнение:

.

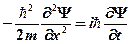Если направление волны не совпадает с осью 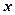, фаза колебаний будет зависеть от координат ( 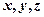). Для этого случая уравнение имеет вид:

.

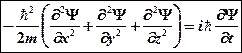С учетом (26), получим стационарное уравнение для свободной частицы:

.

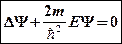Это уравнение совпадает с уравнением Шредингера для случая 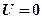, так как мы рассматривали свободную частицу.

Если частица движется в силовом поле, характеризуемом потенциальной энергией 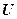, то полная энергия 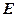складывается из кинетической и потенциальной энергий.

Полная энергия микрочастицы:

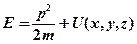, где 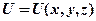не зависит явно от времени.

Уравнение Шредингера для стационарных состояний

.
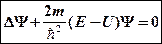