Сила трения действует в общей касательной плоскости к поверхностям соприкасающихся тел и противоположна тому направлению, в котором активно действующие силы стремятся сдвинуть тело.

2. Модуль силы трения при покое принимает всякий раз значение, необходимое для предотвращения проскальзывания тела по поверхности, но не может превзойти некоторого предельного значения, которое достигается на грани перехода тела от состояния покоя к состоянию скольжения: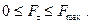

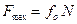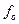3. Максимальное значение силы трения при покое пропорционально нормальному давлению тела на поверхность: , где – коэффициент трения при покое, который определяется экспериментально. Коэффициент 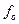зависит от материала тел, шероховатости, влажности, температуры трущихся поверхностей, но на его значение в широких пределах не влияют размеры площадки контакта тел.

4. При скольжении тела по шероховатой поверхности сила трения пропорциональна силе нормальной реакции поверхности: 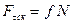и направлена в сторону, противоположную скольжению. Динамический коэффициент трения 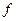(коэффициент трения скольжения), помимо прочего, может зависеть от относительной скорости скольжения.

Пример 3.1.

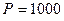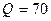Установить, будет ли находиться в покое тело, изображённое на Рис. 3.1, если Н; Н;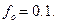

Предположим, что тело находится в покое; тогда уравнения равновесия имеют вид:

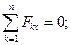
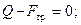
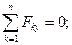
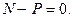
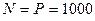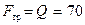Отсюда: Н; Н.

Вычислим максимально возможную силу трения: 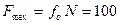Н.

В рассматриваемом случае вычисленная из уравнений равновесия сила трения оказалась меньше максимально возможной, следовательно, условие равновесия 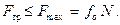выполнено и тело находится в покое и 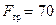Н.

Пример 3.2.

Сохраняя условия предыдущего примера, положим 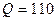Н.

Аналогично примеру 3.1, вычисляем 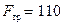Н; 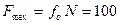Н. Очевидно, что покой нарушится, так как необходимая для предотвращения скольжения сила оказалась больше максимально возможной силы трения. Таким образом, нарушено условие равновесия 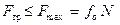, тело придёт в движение, а сила трения примет максимальное значение: 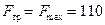Н.

Пример 3.3

Однородный стержень 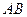опирается на гладкую стену и негладкий пол, образуя с полом угол 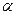(Рис. 3.2). Вес стержня 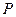. В точке привязан трос, протянутый по полу, который растягивается гирей весом 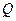. Коэффициент трения 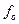. Определить, при каких значениях 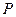возможно равновесие. Трением на блоке 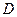пренебречь.

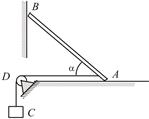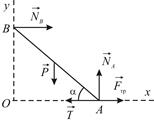Рис. 3.2		Рис. 3.3

При потере равновесия возможно скольжение точки по полу как влево, так и вправо. Найдём сначала минимальное значение 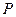, при котором ещё возможно равновесие. Если разгружать тело 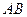(уменьшать 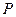), то при потере равновесия точка будет скользить влево. Силовая схема представлена на Рис. 3.3. Составим условия равновесия:

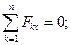
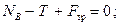
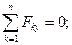
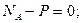
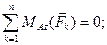
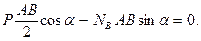
При потере равновесия 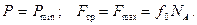Разрешим полученную систему уравнений относительно 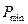. Учитывая, что 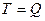, находим: .

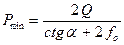При определении 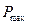заметим, что при потере равновесия точка будет скользить вправо и, следовательно, направление силы трения следует изменить на противоположное, что соответствует изменению знака перед силой трения в полученном выше решении:

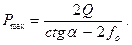
Таким образом, равновесие стержня 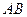возможно, если его вес заключён в пределах

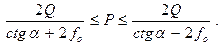
Пример 3.4

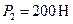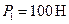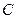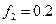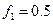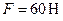На верхней грани прямоугольного бруса , вес которого , находится прямоугольный брус веса . Брус опирается своей нижней гранью на горизонтальную поверхность , причём коэффициент трения между ними (Рис. 3.4). Коэффициент трения между телами и равен . На брус действует сила , образующая с горизонтом угол 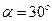. Будет ли брус двигаться относительно ? Будет ли брус двигаться относительно плоскости ?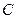

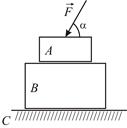Рис. 3.4

Предположим, что верхний брус находится в покое относительно бруса . Уравнения равновесия имеют вид (Рис. 3.5):

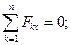
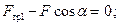
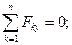
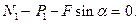
Отсюда: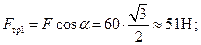

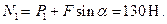
Вычислим максимальную силу трения:

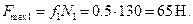
Как видно, сила трения, найденная из уравнений равновесия, т.е. необходимая для обеспечения равновесия тела, меньше максимально возможной силы трения. Следовательно, условие равновесия 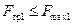выполнено, тело будет покоиться относительно тела , а сила трения оказывается равной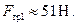

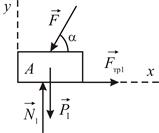Рис. 3.5		Рис. 3.6

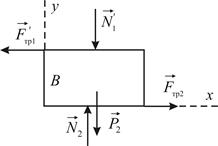
Предположим теперь, что брус покоится относительно опорной плоскости 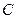. Уравнения равновесия имеют вид (Рис. 3.6):

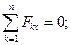
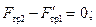
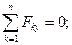
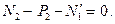
Отсюда, учитывая, что 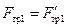и 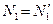, получаем:

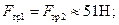
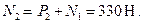
Максимально возможная сила трения равна: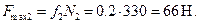

Как видно, сила трения, найденная из уравнений равновесия, т.е. необходимая для обеспечения равновесия тела, меньше максимально возможной силы трения. Следовательно, условие равновесия 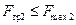выполнено, тело будет покоиться относительно плоскости 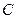, а сила трения оказывается равной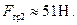

Пример 3.5

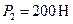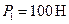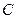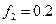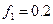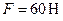На верхней грани прямоугольного бруса , вес которого , находится прямоугольный брус веса . Брус опирается своей нижней гранью на горизонтальную поверхность , причём коэффициент трения между ними (Рис. 3.5). Коэффициент трения между телами и равен . На брус действует сила , образующая с горизонтом угол 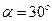. Будет ли брус двигаться относительно ? Будет ли брус двигаться относительно плоскости ?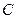

Как видно, по сравнению с предыдущим примером изменился коэффициент трения между телами и . Ход решения задачи остаётся прежним, но изменяются числовые результаты.

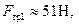Теперь сила трения, необходимая для обеспечения покоя тела относительно тела , осталась прежней – а максимально возможная сила трения оказывается равной

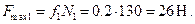
Следовательно, условие равновесия 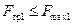не выполнено, тело будет скользить по верхней грани бруса , а сила трения при этом будет максимальной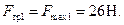

Для бруса получаем: 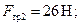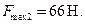Условие равновесия 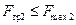выполнено, тело будет покоиться относительно плоскости .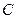

ВОПРОСЫ ДЛЯ САМОКОНТРОЛЯ:

1. Как вычисляется сила трения при относительном покое тел?
2. Как вычисляется сила трения при относительном скольжении тел?

ЗАДАЧИ, РЕКОМЕНДУЕМЫЕ ДЛЯ РАЗБОРА В АУДИТОРИИ И ДЛЯ ЗАДАНИЯ НА ДОМ:

Из сборника задач И.В.Мещерского: 5.2; 5.6; 5.7; 5.9; 5.28; 5.29.

Из учебника «ТЕОРЕТИЧЕСКАЯ МЕХАНИКА - теория и практика»: комплекты СР-12;

СР-13.

ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 8

СИСТЕМА СИЛ В ПРОСТРАНСТВЕ

Для равновесия произвольной системы сил необходимо и достаточно, чтобы сумма проекций всех сил на каждую из трёх взаимно перпендикулярных осей координат равнялась нулю и сумма моментов всех сил системы относительно каждой из этих осей равнялась нулю:

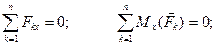
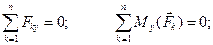
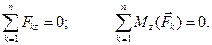
Проведём через точку 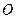, относительно которой вычисляется момент силы, какую-либо ось.