Если система сил имеет равнодействующую, то момент равнодействующей относительно любого центра (любой оси) равен сумме моментов всех сил системы относительно этого центра (этой оси)
Записывая эту теорему для системы сил 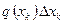 в проекциях на ось
в проекциях на ось 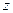 и переходя к пределу при длине отрезков, стремящейся к нулю, получаем:
и переходя к пределу при длине отрезков, стремящейся к нулю, получаем:
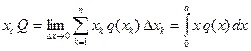
Очевидно, модуль равнодействующей численно равен площади эпюры распределённой нагрузки, а точка её приложения совпадает с центром тяжести однородной пластины, имеющей форму эпюры распределённой нагрузки.
Отметим два часто встречающихся случая.
Равномерно распределённая нагрузка, 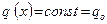 (Рис. 1.30). Модуль равнодействующей и координата её точки приложения определяются по формулам:
(Рис. 1.30). Модуль равнодействующей и координата её точки приложения определяются по формулам:
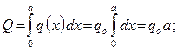
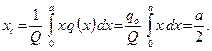
В инженерной практике такая нагрузка встречается довольно часто. Равномерно распределённой в большинстве случаев можно считать весовую и ветровую нагрузку.
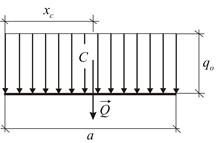 | 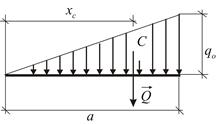 | |
| Рис. 1.30 | Рис. 1.31 |
Линейно распределённая нагрузка, 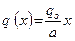 (Рис. 1.31). В этом случае:
(Рис. 1.31). В этом случае:
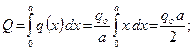
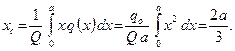
В частности, давление воды на вертикальную стенку прямо пропорционально глубине 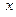 .
.
Пример 1.5
Определить реакции опор  и
и  балки, находящейся под действием двух сосредоточенных сил и равномерно распределённой нагрузки. Дано:
балки, находящейся под действием двух сосредоточенных сил и равномерно распределённой нагрузки. Дано: 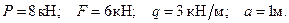
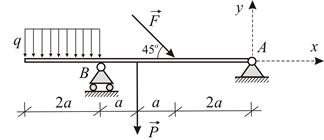 |
| Рис. 1.32 |
Найдём равнодействующую распределённой нагрузки. Модуль равнодействующей равен
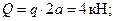
плечо силы 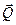 относительно точки
относительно точки  равно
равно 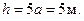 Рассмотрим равновесие балки. Силовая схема представлена на Рис. 1.33.
Рассмотрим равновесие балки. Силовая схема представлена на Рис. 1.33.
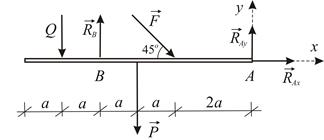 |
| Рис. 1.33 |
Условия равновесия в рассматриваемом случае имеют вид:
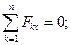
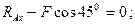
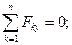
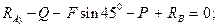
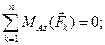
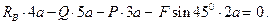
Пример 1.6
Определить реакцию заделки консольной балки, находящейся под действием сосредоточенной силы, пары сил и распределённой нагрузки (Рис. 1.34).
Дано: 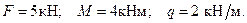
Заменим распределённую нагрузку тремя сосредоточенными силами. Для этого разобъём эпюру распределённой нагрузки на два треугольника и прямоугольник. Находим
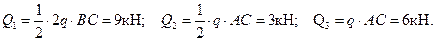
Силовая схема представлена на Рис. 1.35.
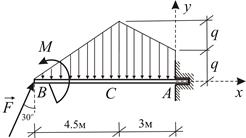 | 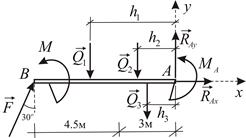 | |
| Рис. 1.34 | Рис. 1.35 |
Вычислим плечи равнодействующих относительно оси 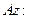
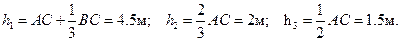
Условия равновесия в рассматриваемом случае имеют вид:
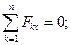
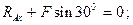
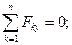
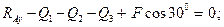
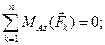
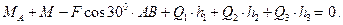
ВОПРОСЫ ДЛЯ САМОКОНТРОЛЯ:
1. Что называется интенсивностью распределённой нагрузки?
2. Как вычислить модуль равнодействующей распределённой нагрузки?
3. Как вычислить координату точки приложения равнодействующей распределённой
нагрузки?
4. Чему равен модуль и какова координата точки приложения равномерно распределённой нагрузки?
5. Чему равен модуль и какова координата точки приложения линейно распределённой нагрузки?
ЗАДАЧИ, РЕКОМЕНДУЕМЫЕ ДЛЯ РАЗБОРА В АУДИТОРИИ И ДЛЯ ЗАДАНИЯ НА ДОМ:
Из сборника задач И.В.Мещерского: 4.28; 4.29; 4.30; 4.33; 4.34.
Из учебника «ТЕОРЕТИЧЕСКАЯ МЕХАНИКА - теория и практика»: комплекты СР-2; СР-3.
ПРАКТИЧЕСКИЕ ЗАНЯТИЯ № 4-5
СТАТИЧЕСКИЙ РАСЧЁТ КУНСТРУКЦИЙ
Равновесие составных тел
При решении задач об определении опорных реакций может оказаться, что из составленных условий равновесия невозможно определить все неизвестные величины, так как их число больше числа уравнений, в которые эти неизвестные входят. Подобное может произойти по двум основным причинам.
Во-первых, на рассматриваемое тело могут быть наложены лишние связи, ненужные для обеспечения равновесия абсолютно твёрдого тела, но необходимые для предотвращения недопустимо больших деформаций. В этом случае задача определения реакций опор является статически неопределимой в том смысле, что невозможно определить реакции связей без учёта деформаций тела, т.е. оставаясь в рамках модели абсолютно твёрдого тела. Такие задачи в теоретической механике не рассматриваются.
Во-вторых, в качестве тела, равновесие которого рассматривается, может быть выбрана конструкция, состоящая из двух или более тел, соединённых между собой внутренними связями. На такую конструкцию заведомо приходится накладывать дополнительные связи, обеспечивающие равновесие конструкции. Основная особенность решения таких задач состоит в том, что необходимо рассматривать равновесие нескольких тел данной конструкции.
Рассмотрим, например, трёх шарнирную арку 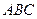 , нагруженную активными силами
, нагруженную активными силами  и
и 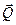 (Рис. 2.1). Можно рассмотреть равновесие арки в целом. Тогда в систему внешних сил войдут заданные силы
(Рис. 2.1). Можно рассмотреть равновесие арки в целом. Тогда в систему внешних сил войдут заданные силы  и
и 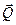 и силы реакций внешних опор – шарниров
и силы реакций внешних опор – шарниров  и
и  . Соответствующая силовая схема представлена на Рис. 2.2.
. Соответствующая силовая схема представлена на Рис. 2.2.
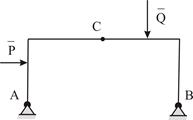 | 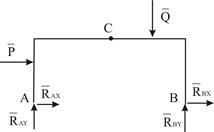 | |
| Рис. 2.1 | Рис. 2.2 |
Хотя такая арка не является абсолютно твёрдым телом, заранее известно, что она покоится и, следовательно, приложенные к ней силы удовлетворяют условиям равновесия. Наличие шарнира 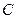 позволяет двум частям арки поворачиваться друг относительно друга. Для предотвращения такого поворота приходится усиливать одну из опор, например, ставить в точке
позволяет двум частям арки поворачиваться друг относительно друга. Для предотвращения такого поворота приходится усиливать одну из опор, например, ставить в точке  шарнирно неподвижную опору вместо шарнирно подвижной. При этом число неизвестных составляющих сил реакций увеличивается – появляется
шарнирно неподвижную опору вместо шарнирно подвижной. При этом число неизвестных составляющих сил реакций увеличивается – появляется 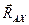 . Трёх уравнений равновесия недостаточно для определения четырёх неизвестных. Поэтому приходится рассматривать равновесие ещё какой-либо части конструкции, например, стержня
. Трёх уравнений равновесия недостаточно для определения четырёх неизвестных. Поэтому приходится рассматривать равновесие ещё какой-либо части конструкции, например, стержня 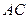 .
.
Для стержня 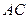 шарнир
шарнир 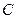 является внешней опорой, поэтому его реакция входит в систему внешних сил, действующих на
является внешней опорой, поэтому его реакция входит в систему внешних сил, действующих на 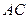 (Рис. 2.3). Для стержня
(Рис. 2.3). Для стержня 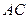 можно составить ещё три уравнения равновесия, которые вместе с уравнениями равновесия, составленными для арки
можно составить ещё три уравнения равновесия, которые вместе с уравнениями равновесия, составленными для арки 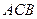 , образуют систему шести уравнений, содержащих шесть
, образуют систему шести уравнений, содержащих шесть
неизвестных.
Можно рассмотреть равновесие правого стержня 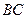 (Рис. 2.4). При этом следует учитывать, что силы взаимодействия в шарнире
(Рис. 2.4). При этом следует учитывать, что силы взаимодействия в шарнире 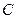 подчиняются третьему закону Ньютона:
подчиняются третьему закону Ньютона: 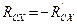 ;
; 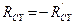 . Для решения поставленной задачи достаточно рассмотреть равновесие только двух из трёх тел в любой комбинации. Условия равновесия третьего тела могут быть использованы для проверки полученных результатов.
. Для решения поставленной задачи достаточно рассмотреть равновесие только двух из трёх тел в любой комбинации. Условия равновесия третьего тела могут быть использованы для проверки полученных результатов.
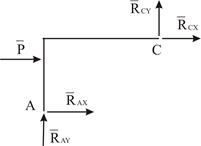 | 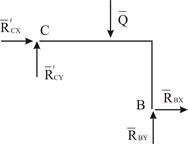 | |
| Рис. 2.3 | Рис. 2.4 |
Универсальный метод решения подобных задач состоит в том, что конструкция разбивается на отдельные абсолютно твёрдые тела и рассматривается равновесие каждого из этих тел. Однако, во многих случаях такой подход оказывается нерациональным, поскольку приводит к необходимости решения системы уравнений, каждое из которых может содержать несколько неизвестных. Причём в уравнения может входить значительное число лишних неизвестных, которые не требуется определять по условиям решаемой задачи. Приобретя определённые навыки, можно поставить целью поиск наиболее рационального способа решения задачи, в основе которого лежит идея использования минимального числа уравнений, каждое из которых, по возможности, содержит только одну неизвестную.
В заключение подчеркнём ещё раз – необходимо рисовать отдельную силовую схему для каждого тела, равновесие которого рассматривается.
Пример 2.1.
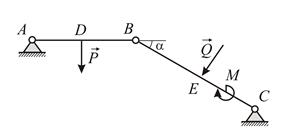 |
| Рис. 2.5 |
Стержневая конструкция нагружена силами  ;
; 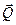 и парой сил с моментом
и парой сил с моментом 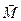 ( Рис. 2.5).
( Рис. 2.5).
Дано: 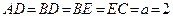 м;
м; 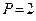 кН;
кН; 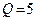 кН;
кН; 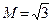 кН м;
кН м; 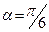 . Определить усилия в шарнирах
. Определить усилия в шарнирах 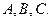
Нужно определить шесть составляющих реакций шарниров. Для получения необходимых для этого шести уравнений можно рассмотреть равновесие всей конструкции и одного из стержней или равновесие каждого из стержней. С точки зрения удобства вычисления плеч сил, предпочтительнее рассмотреть равновесие каждого из стержней.
Рассмотрим равновесие стержня 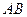 . Силовая схема представлена на Рис. 2.7. Можно составить "стандартную" систему уравнений равновесия:
. Силовая схема представлена на Рис. 2.7. Можно составить "стандартную" систему уравнений равновесия:
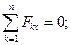
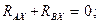
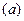
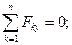
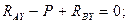
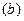
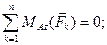
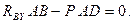
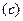
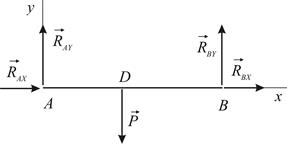 | 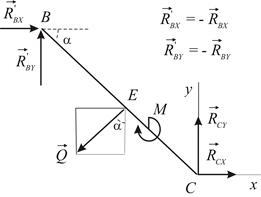 | |
| Рис. 2.6 | Рис. 2.7 |
Нетрудно видеть, что только последнее уравнение 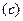 системы позволяет сразу определить неизвестную
системы позволяет сразу определить неизвестную
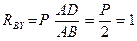 кН
кН
Однако, если составить уравнение
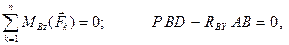
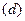
то сразу определяется вторая неизвестная
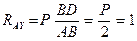 кН
кН
Надобность в уравнении 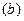 пропадает, уравнение
пропадает, уравнение 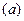 используем в дальнейшем для определения
используем в дальнейшем для определения 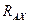 .
.
Рассмотрим равновесие стержня 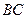 . (При составлении уравнений равновесия учитывается, что
. (При составлении уравнений равновесия учитывается, что 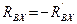 ;
; 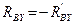 .) Силовая схема представлена на Рис.4.7. Прежде всего, определим
.) Силовая схема представлена на Рис.4.7. Прежде всего, определим 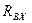 . Для этого составим уравнение
. Для этого составим уравнение
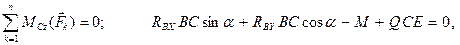
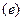
Отсюда
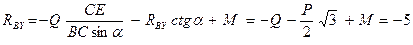 кН.
кН.
Теперь можно использовать уравнение ( 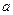 ):
): 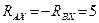 кН Для определения оставшихся неизвестных используем уравнения
кН Для определения оставшихся неизвестных используем уравнения
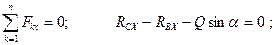
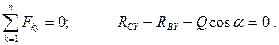
Отсюда: 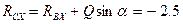 кН;
кН; 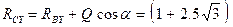 кН.
кН.
Пример 2.2.
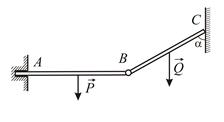 |
| Рис. 2.8 |
Однородные балки 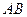 весом
весом 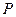 и
и 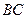 весом
весом 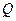 соединены между собой шарниром
соединены между собой шарниром  (Рис. 2.8). Балка
(Рис. 2.8). Балка 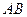 горизонтальна, её левый конец заделан в стену. Балка
горизонтальна, её левый конец заделан в стену. Балка 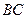 опирается на гладкую вертикальную стену, с которой образует угол
опирается на гладкую вертикальную стену, с которой образует угол 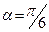 . Дано:
. Дано: 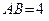 м;
м; 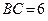 м;
м;  H;
H; 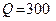 H. Определить реакции опорных стен.
H. Определить реакции опорных стен.
Поскольку по условию задачи не требуется определять усилия во внутреннем шарнире  , имеет смысл рассмотреть равновесие всей конструкции (Рис. 2.9). Составим уравнения равновесия:
, имеет смысл рассмотреть равновесие всей конструкции (Рис. 2.9). Составим уравнения равновесия:
 (
( 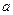 )
)
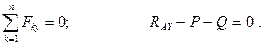 (
( 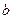 )
)
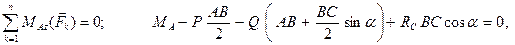 (
( 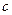 )
)
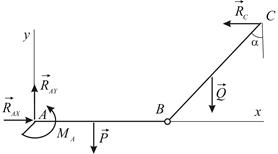 | 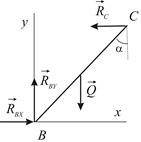 | |
| Рис. 2.9 | Рис. 2.10 |
Только уравнение ( 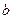 ) позволяет сразу определить
) позволяет сразу определить 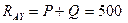 Н. Для вычисления других неизвестных необходимо определить
Н. Для вычисления других неизвестных необходимо определить 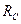 . Рассмотрим равновесие
. Рассмотрим равновесие 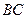 (Рис. 2.10). Составим уравнение:
(Рис. 2.10). Составим уравнение:
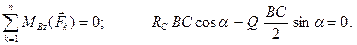
Отсюда:
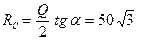 Н.
Н.
Из уравнений ( 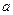 ) и (
) и ( 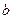 ) находим:
) находим:
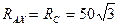 Н;
Н; 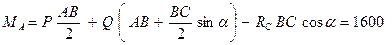 Нм.
Нм.
Пример 2.3.
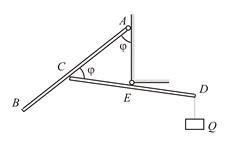 |
| Рис. 2.11 |
Однородный стержень 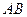 весом
весом 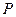 может вращаться вокруг шарнира
может вращаться вокруг шарнира  . Он опирается на такой же стержень
. Он опирается на такой же стержень 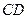 , который может вращаться вокруг оси
, который может вращаться вокруг оси 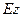 , проходящей через его середину (Рис. 2.11). Точки
, проходящей через его середину (Рис. 2.11). Точки  и
и 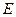 лежат на одной вертикали.
лежат на одной вертикали. 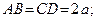
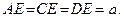 В точке
В точке 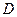 подвешен груз
подвешен груз 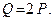 Определить угол
Определить угол 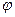 , образуемый стержнем
, образуемый стержнем 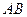 с вертикалью в положении равновесия. Трением пренебречь.
с вертикалью в положении равновесия. Трением пренебречь.
Особенностью задачи является то обстоятельство, что требуется определить только одну неизвестную 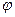 . Другими возможными неизвестными являются четыре составляющие реакций шарниров
. Другими возможными неизвестными являются четыре составляющие реакций шарниров  и
и 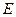 , а также сила взаимной реакции стержней в точке
, а также сила взаимной реакции стержней в точке 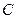 . Для решения задачи принимаем следующую схему.
. Для решения задачи принимаем следующую схему.
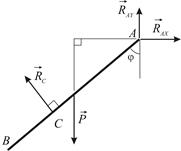
Рассмотрим равновесие стержня 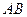 (Рис. 2.12). Составим уравнение моментов относительно оси
(Рис. 2.12). Составим уравнение моментов относительно оси 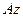 :
:
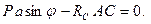
Величину 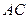 найдём как основание равнобедренного треугольника
найдём как основание равнобедренного треугольника 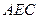 :
:
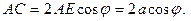
Таким образом,
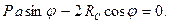 (
( 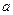 )
)
 |  | |
| Рис. 2.12 | Рис. 2.13 |
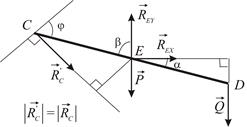
Рассмотрим равновесие стержня 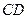 (Рис. 2.13). Составим уравнение моментов относительно оси
(Рис. 2.13). Составим уравнение моментов относительно оси 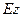 :
:
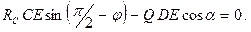
или
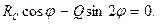 (
( 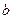 )
)
так как
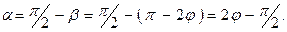
Исключая из уравнений ( 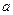 ) и (
) и ( 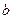 )
) 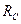 , получаем:
, получаем:
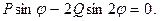 или
или 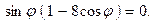
Интерес представляет решение 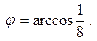
Пример 2.4.
Стержень 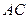 жёстко закреплён в точке
жёстко закреплён в точке  и соединён шарниром
и соединён шарниром 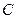 со стержнем
со стержнем 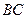 . В точке
. В точке  установлен подвижный шарнир. На стержень
установлен подвижный шарнир. На стержень 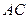 действует линейно распределённая нагрузка максимальной интенсивности
действует линейно распределённая нагрузка максимальной интенсивности 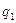 и сила
и сила  . На стержень
. На стержень 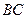 действует однородная распределённая нагрузка интенсивности
действует однородная распределённая нагрузка интенсивности 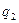 и пара сил с моментом
и пара сил с моментом 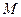 . Размеры указаны на чертеже (Рис. 2.14). Определить реакции опор.
. Размеры указаны на чертеже (Рис. 2.14). Определить реакции опор.
Рассмотрим равновесие всей конструкции. Внешними опорами для 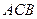 будут жёсткая заделка в точке
будут жёсткая заделка в точке  и шарнир
и шарнир  . Распределённую нагрузку заменяем равнодействующими
. Распределённую нагрузку заменяем равнодействующими 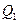 и
и 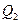 . Силовая схема представлена на Рис. 2.15. Условия равновесия имеют вид:
. Силовая схема представлена на Рис. 2.15. Условия равновесия имеют вид:
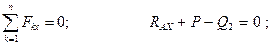
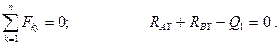
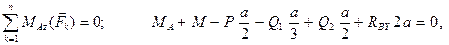
причём, 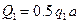 и
и 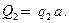
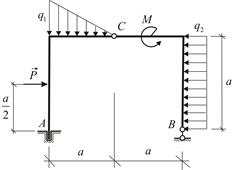 | 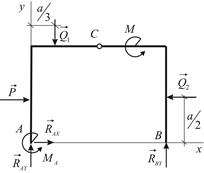 | |
| Рис. 2.14 | Рис. 2.15 |
Полученные три уравнения содержат четыре неизвестные. Это объясняется тем, что условия, являющиеся достаточными для равновесия абсолютно твёрдого тела, использованы для тела деформируемого, для которого они являются только необходимыми. Для получения достаточного количества уравнений рассмотрим равновесие одной из частей конструкции, например, левого стержня 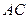 . Для этого стержня внешними силами, помимо прочего, будет и реакция шарнира
. Для этого стержня внешними силами, помимо прочего, будет и реакция шарнира 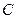 (Рис. 2.16).
(Рис. 2.16).
Условия равновесия имеют вид:
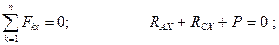
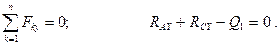
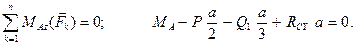
Решая полученную систему уравнений, находим все неизвестные.
Подобная схема решения применима для любых задач о равновесии сочленённых тел. Нетрудно, однако, заметить, что решение полученной системы уравнений связано с определёнными трудностями, поскольку в большинстве уравнений содержится более одной неизвестной. Приобретя определённые навыки в составлении уравнений равновесия, можно поставить задачу составления в каждом конкретном случае наиболее просто решаемой системы уравнений.
Обратимся к разобранному примеру. Можно предложить следующую схему решения задачи.
Тело 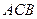 :
: 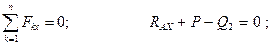
Отсюда: 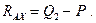
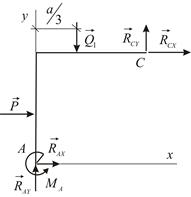 | 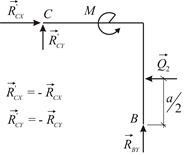 | |
| Рис. 2.16 | Рис. 2.17 |
Тело 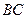 (Рис. 2.17). Учитывая, что
(Рис. 2.17). Учитывая, что 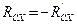 ;
; 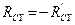 , получаем:
, получаем:
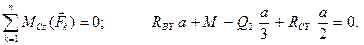
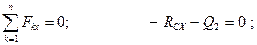
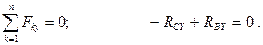
Отсюда: 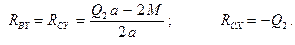
Тело 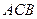 :
:
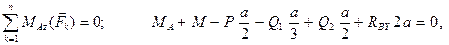
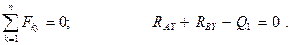
Отсюда: 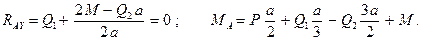
Как видно, таким способом мы можем последовательно определить все неизвестные.
ЗАДАЧИ, РЕКОМЕНДУЕМЫЕ ДЛЯ РАЗБОРА В АУДИТОРИИ И ДЛЯ ЗАДАНИЯ НА ДОМ:
Из сборника задач И.В.Мещерского: 4.32; 4.35; 4.36; 4.37; 4.38; 4.41; 4.42; 4.43; 4.44; 4.53; 4.54; 4.55; 4.56.
Из учебника «ТЕОРЕТИЧЕСКАЯ МЕХАНИКА - теория и практика»: комплекты СР-5; СР-6; СР-7.
ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 6
Расчёт ферм
Особое место в ряду статических задач занимает расчёт ферм. Фермой называется жёсткая конструкция из прямолинейных стержней. Если все стержни фермы и вся приложенная к ней нагрузка расположены в одной плоскости, ферма называется плоской. В дальнейшем будем рассматривать только плоские фермы. Соединения стержней называются узлами фермы.
В результате полного расчёта фермы необходимо определить реакции опор и усилия во всех стержнях фермы.
При расчёте ферм приложенную внешнюю нагрузку (включая весовую нагрузку) заменяют эквивалентной системой, силы которой приложены к узлам фермы. В реальных фермах соединения стержней, как правило, жёсткие (сварка, клёпка и т.д.), так что они не допускают относительного поворота стержней. В расчётной схеме крепления стержней считаются шарнирными, причём, трение в шарнирах считается пренебрежимо малым.
В результате сделанных упрощающих предположений оказывается, что каждый стержень находится в равновесии под действием двух сил, приложенных к его концам. Эти силы должны иметь общую линию действия, т.е. они направлены вдоль стержня. Таким образом, считается, что каждый стержень фермы работает или на растяжение, или на сжатие, но не может испытывать кручения или изгиба. Усилие в стержне считается положительным, если он растянут.
Для определения усилий в стержнях фермы используются два основных метода.
Пример
Рассчитать ферму, изображённую на Рис. 2.18.
Дано: 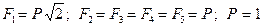 кН;
кН; 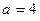 м.
м.
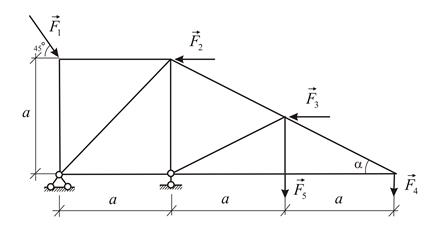 |
| Рис. 2.18 |
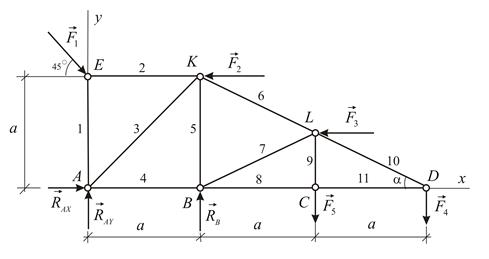
Прежде всего обозначим все узлы и все стержни фермы. Определим реакции опор. Для этого рассмотрим равновесие фермы в целом (Рис. 2.19). Составим условия равновесия:
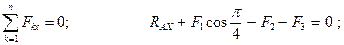
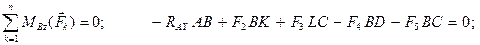
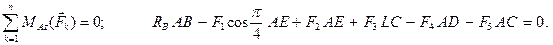
Отсюда:
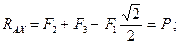
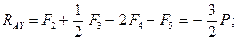
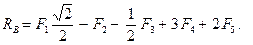
 |
| Рис. 2.19 |
Поскольку вычисленные величины опорных реакций определяют весь дальнейший расчёт, имеет смысл проверить полученные результаты, составив, например, уравнение моментов относительно оси 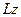 (чтобы в это уравнение вошли все вычисленные величины):
(чтобы в это уравнение вошли все вычисленные величины):
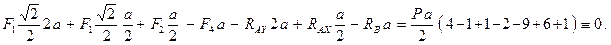
Для определения усилий в стержнях фермы используются два основных метода.
Метод вырезания узлов. Метод состоит в том, что рассматривается равновесие каждого узла фермы в определённой последовательности. На узел действует плоская система сходящихся сил, для которой можно составить два уравнения равновесия, что позволяет определить две неизвестные. Поэтому расчёт начинают с узла, соединяющего два стержня фермы. Затем переходят к соседним узлам в определённой последовательности, которая позволяет на каждом шаге определять усилия в очередных двух стержнях. Первоначально предполагается, что стержни растянуты, т.е. их реакции направлены от узлов. Если усилие в каком-либо стержне оказывается отрицательным, то это означает, что данный стержень сжат.
Заметим, что уравнения равновесия фермы в целом являются прямым следствием полной системы уравнений равновесия узлов, так что методом вырезания узлов можно определить в том числе и реакции опор фермы. Но в этом случае часто приходится совместно решать систему, содержащую значительное число уравнений. Предварительное определение реакций опор упрощает решение задачи, а неиспользованные уравнения равновесия узлов можно рассматривать как проверочные.
Рассмотрим равновесие узла 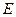
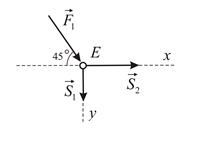
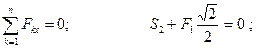
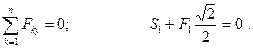
Отсюда: 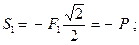 (стержень сжат)
(стержень сжат)
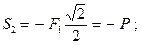 (стержень сжат).
(стержень сжат).
Рассмотрим равновесие узла 
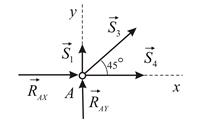
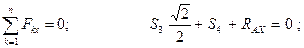
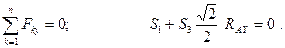
Отсюда:
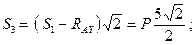 (стержень растянут)
(стержень растянут)
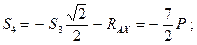 (стержень сжат).
(стержень сжат).
Рассмотрим равновесие узла 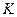
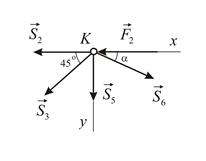
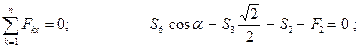
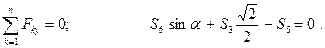
Значения тригонометрических функций определим из треугольника 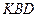 :
:
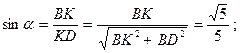
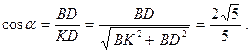
Таким образом,
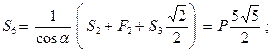 (стержень растянут)
(стержень растянут)
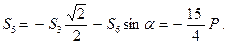 (стержень сжат).
(стержень сжат).
Рассмотрим равновесие узла 
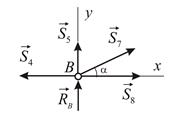
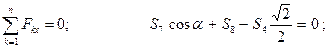
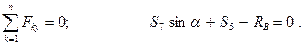
Отсюда:
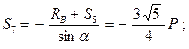 (стержень сжат).
(стержень сжат).
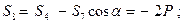 (стержень сжат).
(стержень сжат).
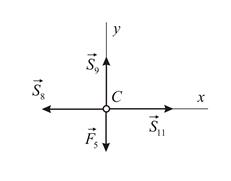 Рассмотрим равновесие узла
Рассмотрим равновесие узла 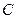
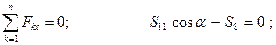

Отсюда:
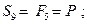 (стержень растянут)
(стержень растянут)
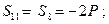 (стержень сжат).
(стержень сжат).
Рассмотрим равновесие узла 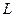
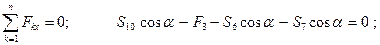
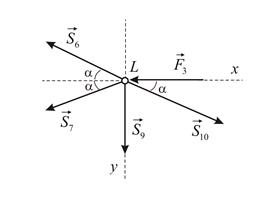
Отсюда:
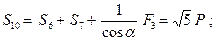 (стержень растянут)
(стержень растянут)
Таким образом, определены усилия во всех стержнях фермы. Оставшиеся уравнения используем для проверки полученных результатов.
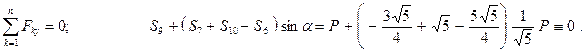
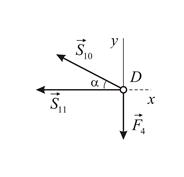 Рассмотрим равновесие узла
Рассмотрим равновесие узла 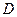
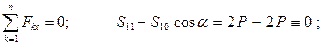
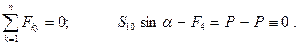
Метод сквозных сечений (метод Риттера). Этим методом удобно пользоваться для определения усилий в отдельных стержнях фермы, в частности для проверочных расчётов. Идея метода состоит в том, что ферма разделяется сечением на две части и рассматривается равновесие одной из этих частей. Сечение проводится по трём стержням фермы, в которых (или в одном из которых) требуется определить усилие. Действие отброшенной части фермы заменяют соответствующими реакциями, направляя их вдоль разрезанных стержней от узлов, т.е. считая стержни растянутыми (как и в методе вырезания узлов). Условия равновесия составляются так, чтобы в каждое уравнение входила только одна неизвестная величина.
Если сечение проводится более, чем по трём стержням, то усилия в "лишних" стержнях должны быть определены предварительно. В противном случае будет необходимо рассмотреть комбинацию из нескольких сечений или комбинацию метода сечений и метода вырезания узлов.
В качестве примера проведём сечение через шестой, седьмой и восьмой стержни. Рассмотрим равновесие правой части фермы (Рис. 2.20).
Уравнения равновесия имеют вид:
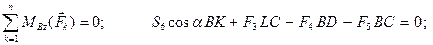
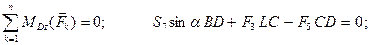
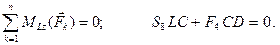
Отсюда:
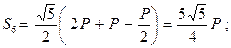
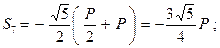
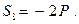
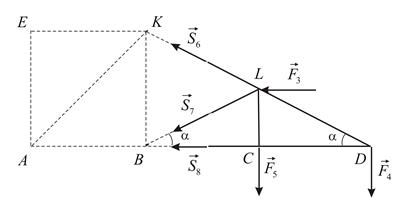 |
| Рис. 2.20 |
Условие жёсткости фермы. Найдём минимальное число стержней 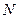 , которое необходимо для образования плоской фермы, имеющей
, которое необходимо для образования плоской фермы, имеющей 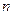 узлов. Простейшая ячейка фермы (треугольник) имеет три стержня и три узла. Для присоединения каждого из оставшихся
узлов. Простейшая ячейка фермы (треугольник) имеет три стержня и три узла. Для присоединения каждого из оставшихся 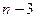 узлов необходимо два стержня. Таким образом, условие жёсткости фермы имеет вид:
узлов необходимо два стержня. Таким образом, условие жёсткости фермы имеет вид: 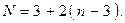
Условие статической определимости фермы. Ферма является статически определимой, если число неизвестных совпадает с числом независимых уравнений равновесия, в которые эти неизвестные входят. Для плоской фермы, имеющей 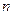 узлов, можно составить
узлов, можно составить 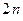 уравнений равновесия, три из которых расходуются на определение трёх составляющих реакций опор. Для определения усилий в стержнях фермы остаётся
уравнений равновесия, три из которых расходуются на определение трёх составляющих реакций опор. Для определения усилий в стержнях фермы остаётся 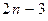 уравнения. Таким образом, условие статической определимости фермы совпадает с условием её жёсткости.
уравнения. Таким образом, условие статической определимости фермы совпадает с условием её жёсткости.
Методы расчёта фермы рассмотрим на примере.
ВОПРОСЫ ДЛЯ САМОКОНТРОЛЯ:
- В чём суть упрощающих предположений, принимаемых при расчёте фермы?
- В чём состоит метод вырезания узлов?
- В чём состоит метод сквозных сечений?
- Каково условие жёсткости фермы?
- Каково условие статической определимости фермы?
ЗАДАЧИ, РЕКОМЕНДУЕМЫЕ ДЛЯ РАЗБОРА В АУДИТОРИИ И ДЛЯ ЗАДАНИЯ НА ДОМ:
Из сборника задач И.В.Мещерского: 4.66; 4.67; 4.68; 4.70; 4.71; 4.73; 4.74.
Из учебника «ТЕОРЕТИЧЕСКАЯ МЕХАНИКА - теория и практика»: комплекты СР-8; СР-9; СР-10; СР-11.
ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 7
СИЛА ТРЕНИЯ
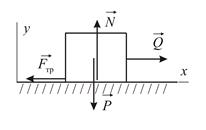 |
| Рис. 3.1 |
Свойства силы трения устанавливаются по результатам следующего эксперимента. На горизонтальной поверхности находится тело, к которому приложены две активные силы: нормальная к поверхности сила  , модуль которой в ходе эксперимента не изменяется (например, сила тяжести), и сила
, модуль которой в ходе эксперимента не изменяется (например, сила тяжести), и сила 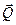 направленная параллельно поверхности, модуль которой в ходе эксперимента постепенно увеличивается (Рис. 3.1). Со стороны поверхности возникают в ответ нормальная реакция
направленная параллельно поверхности, модуль которой в ходе эксперимента постепенно увеличивается (Рис. 3.1). Со стороны поверхности возникают в ответ нормальная реакция 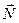 и сила трения
и сила трения 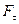 .
.
Установленные в результате обработки описанного эксперимента закономерности сводятся к следующим положениям (законы Амантона-Кулона).
