Учёт пары сил при составлении уравнений равновесия

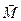Рассмотрим особенности решения задач, в которых наряду с силами на тело действует пара сил с моментом , расположенная в координатной плоскости .

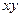При составлении уравнений равновесия следует учитывать, что в условия равенства нулю суммы проекций всех сил на любую координатную ось входящие в пару силы 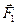и 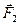никакого вклада не внесут, так как сумма проекций этих сил на любую координатную ось равна нулю ( ).

Вычислим сумму моментов сил, образующих пару, относительно оси 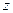(Рис. 1.21).

Рис. 1.21

Таким образом, в уравнении моментов к моментам прочих сил алгебраически прибавляется момент пары, точнее проекция на ось 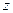вектора момента пары, взятая с соответствующим знаком. Проекция момента пары положительна, если с положительного конца оси 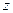поворот пары виден против хода часовой стрелки.

Пример 1.3

Однородная балка 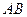весом 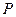, шарнирно закреплённая в точке , удерживается в горизонтальном положении при помощи троса. Балка нагружена парой сил с моментом 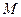(Рис. 1.22). Дано: Н; Нм; м; 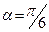. Определить давление на шарнир и натяжение троса.

Рассмотрим равновесие балки 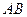. Силовая схема представлена на Рис. 1.23. Заметим, что необходимо определить силы, приложенные не к балке 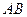, а к другим телам – шарниру и тросу. Мы рассматриваем равновесие балки и поэтому ввели силы реакции шарнира и реакции троса . Но эти реакции, согласно третьему закону Ньютона, равны по модулю и противоположны по направлению искомым силам.

Рис. 1.22		Рис. 1.23

При составлении уравнения моментов за моментную примем точку и заметим, что поворот, создаваемый парой сил, виден по ходу часовой стрелки.

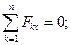
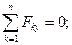
Отсюда:

Н; Н; Н.

Давление на шарнир определим по формуле:

Н.

Жёсткая заделка.

Рассмотрим балку, один конец которой заделан в стену (Рис. 1.24). Подобно неподвижному шарниру, жёсткая заделка препятствует любым перемещениям конца балки и, следовательно, создаёт неизвестную по модулю и направлению силу реакции. Но в отличие от шарнира, заделка препятствует любым поворотам балки, создавая кроме силы реакции ещё и пару сил, направление и модуль момента которой заранее неизвестны. Таким образом, в общем случае получаем в качестве неизвестных три проекции силы реакции на координатные оси и три момента реакции относительно координатных осей.

Рис. 1.24		Рис. 1.25

Особый интерес представляет случай, когда система активных сил расположена в одной плоскости (например, в координатной плоскости 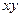. В этом случае система сил реакций также будет плоской и реакция заделки будет представлена двумя составляющими силы и и одной составляющей момента (Рис. 1.25). Неизвестными величинами в таком случае будут проекции этих составляющих на соответствующие координатные оси.

Пример 1.4

Однородная балка 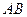весом 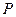, защемлена в стене в сечении . Балка нагружена силой 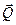, приложенной в точке (Рис. 1.26). Определить составляющие реакции заделки.

Рис. 1.26		Рис. 1.27

Рассмотрим равновесие балки 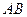. Силовая схема представлена на Рис. 1.27.

Условия равновесия имеют вид:

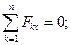
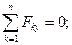
ВОПРОСЫ ДЛЯ САМОКОНТРОЛЯ:

1. Какой вклад вносит пара сил в уравнения равновесия?

2. Какими составляющими представляется реакция жёсткой заделки?

ЗАДАЧИ, РЕКОМЕНДУЕМЫЕ ДЛЯ РАЗБОРА В АУДИТОРИИ И ДЛЯ ЗАДАНИЯ НА ДОМ:

Из сборника задач И.В.Мещерского: 4.25; 4.27.

Из учебника «ТЕОРЕТИЧЕСКАЯ МЕХАНИКА - теория и практика»: комплекты СР-2; СР-3

ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 3

Распределённая нагрузка

Поверхностные и объёмные силы представляют собой нагрузку, распределённую по некоторой поверхности или объёму. Такая нагрузка задаётся интенсивностью , которая представляет собой силу, приходящуюся на единицу некоторого объёма, или некоторой площади, или некоторой длины.

Особое место при решении ряда практически интересных задач занимает случай плоской распределённой нагрузки, приложенной по нормали к некоторой балке. Если вдоль балки направить ось 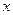, то интенсивность будет функцией координаты 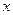и измеряется в Н/м. Интенсивность представляет собой силу, приходящуюся на единицу длины.

Плоская фигура, ограниченная балкой и графиком интенсивности нагрузки, называется эпюрой распределённой нагрузки (Рис. 1.28). Если по характеру решаемой задачи можно не учитывать деформации, т.е. можно считать тело абсолютно твёрдым, то распределённую нагрузку можно (и нужно) заменить равнодействующей.

Рис. 1.28		Рис. 1.29

Разобьём балку на 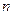отрезков длиной , на каждом из которых будем считать интенсивность постоянной и равной , где – координата отрезка . При этом кривая интенсивности заменяется ломаной линией, а нагрузка, приходящаяся на отрезок , заменяется сосредоточенной силой 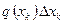, приложенной в точке (Рис. 1.29). Полученная система параллельных сил имеет равнодействующую, равную сумме сил, действующих на каждый из отрезков, приложенную в центре параллельных сил.

Понятно, что такое представление тем точнее описывает реальную ситуацию, чем меньше отрезок , т.е. чем больше число отрезков 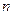. Точный результат получаем, переходя к пределу при длине отрезка , стремящейся к нулю. Предел, получаемый в результате описанной процедуры, представляет собой интеграл. Таким образом, для модуля равнодействующей получаем:

Для определения координаты точки 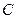приложения равнодействующей используем теорему Вариньона: