Четырёхполюсник – общее обозначение

Схемы замещения четырёхполюсников

Коэффициенты уравнений четырёхполюсников

Системы уравнений четырёхполюсников

ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ ЧЕТЫРЁХПОЛЮСНИКОВ

ЛЕКЦИЯ 19

План лекции:

19.1. Основные определения и классификация четырёхполюсников

19.1. Основные определения и классификация четырёхполюсников

Электрическую цепь или её часть, рассматриваемые относительно двух пар выводов, называют четырёхполюсником (рис. 19.1).

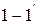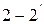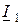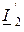Входную (первичную) пару выводов четырёхполюсника обозначают цифрами , выходную (вторичную) – . В качестве положительных принимают направления напряжений от верхних выводов к нижним, а токов – втекающими. В отдельных случаях положительными считают вытекающие токи. Вариант с положительными токами и называют прямой передаче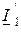й, и 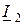– обратной, втекающими токам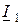и и 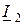– комбинированной. Сочетание токов 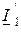и 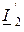специального названия не имеет и применяется редко.

В случае гармонических сигналов теория четырёхполюсников позволяет производить анализ и синтез цепей различных как по структуре и сложности, так и по принципу работы, не рассчитывая токи и напряжения всех реальных элементов внутри четырёхполюсников, что весьма упрощает и ускоряет получение результата. Например, сложную электрическую цепь можно представить в виде совокупности соединённых друг с другом исходных четырёхполюсников. Теория позволяет найти параметры эквивалентного обобщающего четырёхполюсника и рассчитать его входные и выходные сопротивления по известным параметрам исходного четырёхполюсника.

Различают линейные и нелинейные четырёхполюсники.

Четырёхполюсник называют линейным, если в его состав входят элементы только с линейными вольтамперными характеристиками. Четырёхполюс­ник называют нелинейным, если он содержит хотя бы один нелинейный элемент.

По наличию или отсутствию внутренних источников энергии четы­рёхполюсники делят на активные (автономные и неавтономные) и пассивные.

Активными автономныминазывают четырёхполюсники, содержащие независимые некомпенсированные источники эдс или тока. Независимыми называют источники, которые создают в ветвях четырёхполюсника токи и напряжения при отсутствии внешнего сигнала. Источник называют некомпенсированным, если между выводами четырёхполюсника существуют напряжения при отсутствии внешних цепей.

Активными неавтономными называют четырёхполюсники, содержащие зависимые источники эдс или тока как в сочетании с независимыми компенсированными источниками, так и без них. Генераторы эдс и тока, действие которых проявляется только при наличии внешних источников сигнала, называют зависимыми или неавтономными. К активным неавтономным относят, например, четырёхполюсники, содержащие транзисторы.

Четырёхполюсники называют пассивными, если они не содержат источников электрической энергии или являются линейными и содержат независимые компенсированные источники. При отсутствии внешних сигналов у пассивных четырёхполюсников напряжения между двумя любыми выводами равны нулю.

Четырёхполюсники делят на обратимые и необратимые.

Четырёхполюсник называют обратимымили взаимным, если для него выполняется принцип взаимности: отношение напряжения на входе к току на выходе не зависит от того, какая из двух пар выводов является входной и какая выходной.

Четырёхполюсники могут быть симметричными и несимметричными.

Четырёхполюсник называют симметричным, если перемена местами его входных и выходных зажимов не изменяет токов и напряжений во внешних цепях. Симметричные четырёхполюсники всегда обратимы. Электрическая симметрия не требует геометрической (топологической) симметрии его схемы. Однако если обратимый четырёхполюсник имеет топологическую симметрию, то одновременно обязательно существует электрическая симметрия.

Пассивные линейные четырёхполюсники всегда являются обратимыми.

Активные четырёхполюсники могут быть как обратимыми, так и необратимыми, причём активные несимметричные четырёхполюсники являются необратимыми.

Характеристики четырёхполюсника полностью описываются входными и выходными токами и напряжениями. Выбирая две любые из этих величин в качестве независимых, две оставшиеся можно выразить через них в виде системы из двух линейных алгебраических уравнений. Систему уравнений четырёхполюсника можно записать в виде одной из шести форм, что определяется выбранным сочетанием независимых величин.

1. ФормаY-параметров или, более кратко, форма .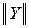

Здесь независимыми считают напряжения 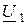и 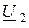, а зависимыми – ток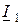и и :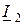

или в матричной записи

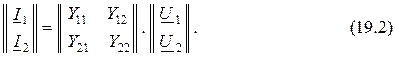
2. ФормаZ-параметров или :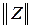

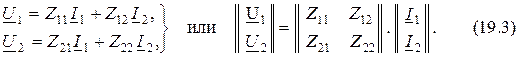
3. Форма A-параметров или :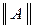

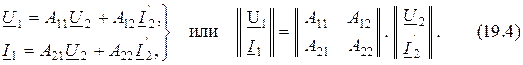
4. ФормаH-параметров или :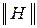

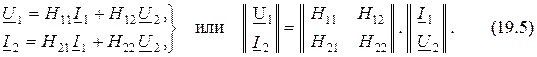
Если в качестве независимых выбраны 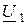и 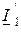, то система уравнений будет записана в 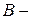параметрах, если независимыми являются 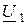и 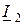, то – в 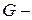параметрах.

Коэффициенты уравнений четырёхполюсника являются его первичными параметрами.

Выбор системы уравнений определяется в основном удобством экспериментального нахождения параметров. А именно, в качестве независимых токов и напряжений принимают те, которые для данного четырёхполюсника наиболее удобно изменять в процессе измерений, что однозначно определяет тип параметров и форму системы уравнений.

Чаще других применяют 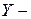, , 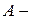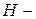и 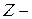параметры. Например, свойства транзисторов в справочниках описывают через 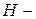параметры, так как наиболее удобно изменять ток базы 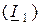и напряжение между коллектором и эмиттером .

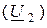Коэффициенты одной системы уравнений могут быть выражены через коэффициенты любой другой.

Пусть, например, известны 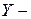параметры четырёхполюсника, а требуется найти его 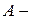параметры.

Для решения задачи преобразуем второе уравнение системы (19.1) к виду (19.4)

Подставим это уравнение в первое выражение из (19.1) и после преобразования получим

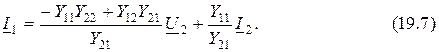
Сравнивая уравнения (19.6) и (19.7) с системой уравнений (19.4) и учитывая, что 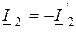, получаем

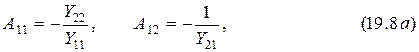
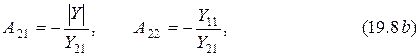
где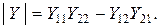

Поэтому достаточно знать параметры четырёхполюсника в какой-либо одной форме записи, чтобы получить их в любой другой. В литературе [1] и [3] имеются таблицы, облегчающие переход от одного вида параметров к другому.

К теме 1.4