Метод эквивалентных сопротивлений и его применений для расчета электрических цепей

Метод эквивалентных сопротивлений и его применений для расчета электрических цепей

И 2 законы Кирхгофа и их применение для расчета электрических цепей

Первый закон Кирхгофа вытекает из закона сохранения заряда. Он состоит в том, что алгебраическая сумма токов, сходящихся в любом узле, равна нулю.

где – число токов, сходящихся в данном узле. Например, для узла электрической цепи (рис. 1) уравнение по первому закону Кирхгофа можно записать в виде I1 - I2 + I3 - I4 + I5 = 0

Рис. 1

В этом уравнении токи, направленные к узлу, приняты положительными.

Первое правило Кирхгофа гласит, чтоалгебраическая сумматоковветвей, сходящихся в каждом узле любой цепи равна нулю. При этом направленный к узлу ток принято считать положительным, а направленный от узла — отрицательным: Алгебраическая сумма токов, направленных к узлу, равна сумме направленных от узла.

{\displaystyle \sum \limits _{j=1}^{n}I_{j}=0.}

Иными словами, сколько тока втекает в узел, столько из него и вытекает. Это правило следует из фундаментальногозакона сохранения заряда.

Второй закон Кирхгофа:алгебраическая сумма падений напряжений на отдельных участках замкнутого контура, произвольно выделенного в сложной разветвленной цепи, равна алгебраической сумме ЭДС в этом контуре

Где k – число источников ЭДС; m – число ветвей в замкнутом контуре; Ii, Ri – ток и сопротивление i-й ветви.

Рис. 2

Так, для замкнутого контура схемы (рис. 2) Е1 - Е2 + Е3 = I1R1 - I2R2 + I3R3 - I4R4

Второе правило Кирхгофа (правило напряжений Кирхгофа) гласит, что алгебраическая сумма напряжений на резистивных элементах замкнутого контура, равна алгебраической сумме ЭДС, входящих в этот контур. Если в контуре нет источников ЭДС (идеализированных генераторов напряжения), то суммарное падение напряжений равно нулю:

для постоянных напряжений {\displaystyle \sum _{k=1}^{n}E_{k}=\sum _{k=1}^{m}U_{k}=\sum _{k=1}^{m}R_{k}I_{k};}

для переменных напряжений {\displaystyle \sum _{k=1}^{n}e_{k}=\sum _{k=1}^{m}u_{k}=\sum _{k=1}^{m}R_{k}i_{k}+\sum _{k=1}^{m}u_{L\,k}+\sum _{k=1}^{m}u_{C\,k}.}

Метод суперпозиции

Применяется только для линейных цепей. Основан на использовании принципа суперпозиции.

1. Принцип суперпозиции: ток, протекающий под воздействием нескольких ЭДС, равен алгебраической сумме частичных токов, протекающих от каждой из ЭДС в отдельности.

Алгоритм:

1. Оставляем в цепи одну ЭДС, все остальные полагаем равными нулю, и рассчитываем частичные токи, протекающие под воздействием этой ЭДС.

2. Оставляем в цепи другую ЭДС, остальные полагаем равными нулю, и рассчитываем частичные токи.

3. И так далее столько раз, сколько ЭДС.

4. Действительный ток, протекающий под воздействием всех ЭДС, определяем как алгебраическую сумму частичных токов.

Этот метод рационально использовать, когда число ЭДС много меньше числа ветвей.
Рассмотрим пример расчета:

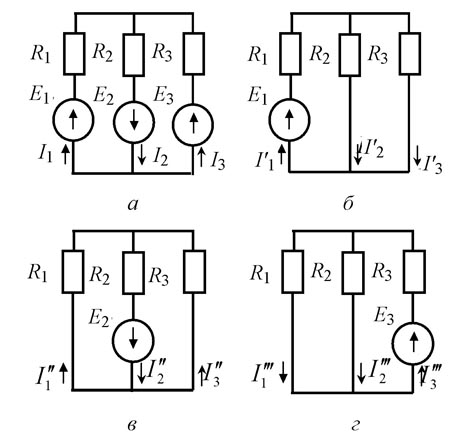
Рис. 1.9. Исходная схема (а) и схемы для определения
частичных токов (б – г)

– рассчитываем цепь и находим 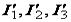(рис. 1.9, б);
– рассчитываем цепь и находим 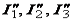(рис. 1.9, в);
– рассчитываем цепь и находим 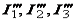(рис. 1.9, г);
– на заключительном этапе определяем

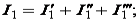
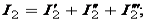
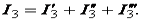
Знаки у частичных токов берем с учетом их направления.

4. Соединение проводников треугольником и звездой и методы их эквивалентных преобразований

Соединение треугольником

При соединении треугольником конец одной обмотки соединяется с началом другой. Таким образом, образуется замкнутый контур.

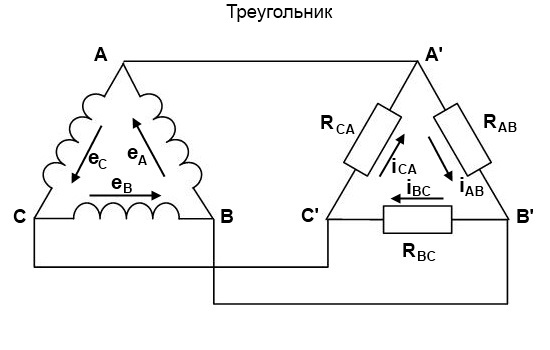В таком соединении каждая фаза находится под линейным напряжением, то есть линейные и фазные напряжения равны

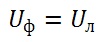
А фазные и линейные токи соотносятся как

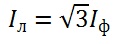
Соединение звездой

При соединении обмоток звездой все три фазы имеют одну общую точку – ноль. При этом такая система может быть трехпроводной или четырехпроводной. В последнем случае используется нулевой провод. Нулевой провод не нужен, если система симметрична, то есть токи в фазах такой системы одинаковы. Но если нагрузка несимметрична, то фазные токи различны, и в нулевом проводе возникает ток, который равен векторной сумме фазных токов

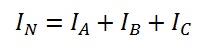
Также, нулевой провод может выступать в роле одной из фаз, если она выйдет из строя, это предотвратит выход из строя всей системы. Правда нужно учитывать, что нулевой провод не рассчитан на подобные нагрузки, и в целях экономии металла и изоляции он изготавливает под более малые токи, чем в фазах.

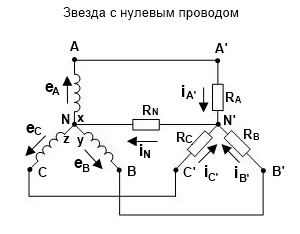
В трехфазных цепях существуют так называемые фазные и линейные напряжения и токи.

Фазное напряжение – это разность потенциалов между нулевой точкой и линейным проводом. То есть, проще говоря, фазное напряжение - это напряжение на фазе.

Линейное напряжение – это разность потенциалов между линейными проводами.

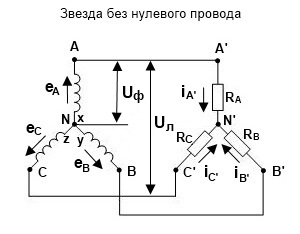
При соединении звездой фазные и линейные напряжения соотносятся как

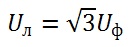
А фазные и линейные токи при симметричной нагрузке одинаковы

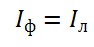
К теме1.3

Основные понятия

Контурный ток - это величина, которая одинакова во всех ветвях данного контура. Обычно в расчетах они обозначаются двойными индексами, например I₁₁, I₂₂ и тд.

Действительный ток в определенной ветви определяется алгебраической суммой контурных токов, в которую эта ветвь входит. Нахождение действительных токов и есть первоочередная задача метода контурных токов.

Контурная ЭДС - это сумма всех ЭДС входящих в этот контур.

Собственным сопротивлением контура называется сумма сопротивлений всех ветвей, которые в него входят.

Общим сопротивлением контура называется сопротивление ветви, смежное двум контурам.

Общий план составления уравнений

1 – Выбор направления действительных токов.

2 – Выбор независимых контуров и направления контурных токов в них.

3 – Определение собственных и общих сопротивлений контуров

4 – Составление уравнений и нахождение контурных токов

5 – Нахождение действительных токов

Итак, после ознакомления с теорией предлагаем приступить к практике! Рассмотрим пример.

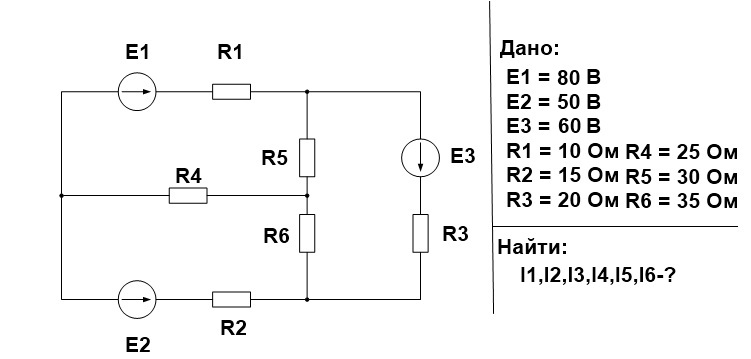
Выполняем все поэтапно.

1. Произвольно выбираем направления действительных токов I₁-I₆.

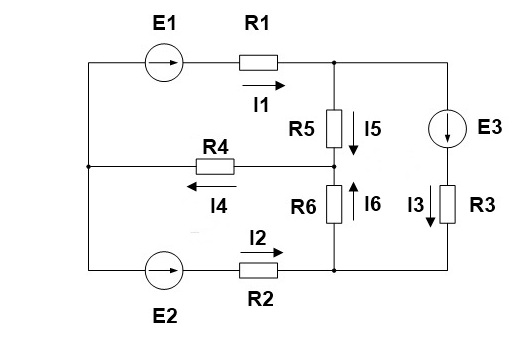
2.Выделяем три контура, а затем указываем направление контурных токов I₁₁,I₂₂,I₃₃. Мы выберем направление по часовой стрелке.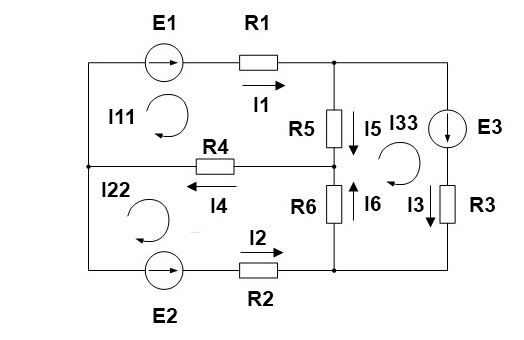

3. Определяем собственные сопротивления контуров. Для этого складываем сопротивления в каждом контуре.

R₁₁=R₁+R₄+R₅=10+25+30= 65 Ом

R₂₂=R₂+R₄+R₆=15+25+35 = 75 Ом

R₃₃=R₃+R₅+R₆=20+30+35= 85 Ом

Затем определяем общие сопротивления, общие сопротивления легко обнаружить, они принадлежат сразу нескольким контурам, например сопротивление R₄ принадлежит контуру 1 и контуру 2. Поэтому для удобства обозначим такие сопротивления номерами контуров к которым они принадлежат.

R₁₂=R₂₁=R₄=25 Ом

R₂₃=R₃₂=R₆=35 Ом

R₃₁=R₁₃=R₅=30 Ом

4. Приступаем к основному этапу – составлению системы уравнений контурных токов. В левой части уравнений входят падения напряжений в контуре, а в правой ЭДСисточников данного контура.

Так как контура у нас три, следовательно, система будет состоять из трех уравнений. Для первого контура уравнение будет выглядеть следующим образом:

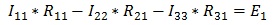
Ток первого контура I₁₁, умножаем на собственное сопротивление R₁₁ этого же контура, а затем вычитаем ток I₂₂, помноженный на общее сопротивление первого и второго контуров R₂₁ и ток I₃₃, помноженный на общее сопротивление первого и третьего контура R₃₁. Данное выражение будет равняться ЭДС E₁ этого контура. Значение ЭДС берем со знаком плюс, так как направление обхода (по часовой стрелке) совпадает с направление ЭДС, в противном случае нужно было бы брать со знаком минус.

Те же действия проделываем с двумя другими контурами и в итоге получаем систему:

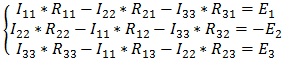
В полученную систему подставляем уже известные значения сопротивлений и решаем её любым известным способом.

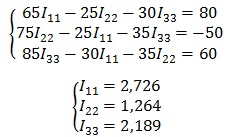
5. Последним этапом находим действительные токи, для этого нужно записать для них выражения.

Контурный ток равен действительному току, который принадлежит только этому контуру. То есть другими словами, если ток протекает только в одном контуре, то он равен контурному.

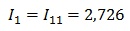
Но, нужно учитывать направление обхода, например, в нашем случае ток I2 не совпадает с направлением, поэтому берем его со знаком минус.

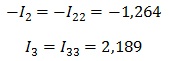
Токи, протекающие через общие сопротивления определяем как алгебраическую сумму контурных, учитывая направление обхода.

Например, через резистор R₄ протекает ток I₄, его направление совпадает с направлением обхода первого контура и противоположно направлению второго контура. Значит, для него выражение будет выглядеть

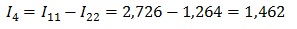
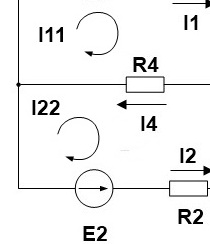
А для остальных

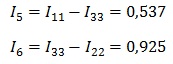
Так решаются задачи методом контурных токов. Надеемся что вам пригодится данный материал, удачи!

Метод узловых потенциалов

Метод узловых потенциалов – один из методов анализа электрической цепи, который целесообразно использовать, когда количество узлов в цепи меньше или равно числу независимых контуров. Данный метод основан на составлении уравнений по первому закону Кирхгофа. При этом, потенциал одного из узлов цепи принимается равным нулю, что позволяет сократить число уравнений до n-1.

Рассмотрим пример

1 – Для начала примем узел 4 за базовый и будем считать его потенциал равным нулю.

2 - Составим уравнения по первому закону Кирхгофа для узла 1,2,3 (для узла 4 не составляем, так как это не требуется)

3 – Используя обобщённый закон Ома составим уравнения для нахождения каждого из токов (за ϕ_i берем потенциал узла из которого ток выходит, а за ϕ потенциал узла в который ток входит) G_i – проводимость i-ой ветви.

4 – Подставим полученные выражения для токов в уравнения из пункта 2, получим

Данная система уравнений записана для цепи состоящей из 4 узлов, а для n узлов справедливо

Проводимости G₁₁,G₂₂ и т.д. – сумма проводимостей сходящихся в узле (собственные проводимости), всегда берутся со знаком плюс. Проводимости G₁₂,G₂₁ и т.д. проводимости ветвей соединяющих узлы (общие проводимости), всегда берутся со знаком минус.

Если источник тока или ЭДС направлен к узлу, то берем со знаком плюс, в противном случае со знаком минус.

5 – Решив систему уравнений из пункта 4 любым доступным способом, найдем неизвестные потенциалы в узлах, а затем определим с помощью них токи.

Правильность решения проверим с помощью баланса мощностей

Эквивалентный генератор. Определение ЭДС и внутреннего сопротивления эквивалентного генератора(ЭГ). Расчет цепей методом ЭГ

Р е ш е н и е.

а) Расчет режима холостого хода.

Убираем третью ветвь, оставляя зажимы m и n разомкнутыми (рис. 1.21, а). Напряжение между ними, равное U_X, находится как падение напряжения на сопротивлении R2:

б) Расчет режима короткого замыкания. Замыкаем накоротко зажимы m и n (рис. 1.21, б). Ток короткого замыкания:Ik=E1/R1=75 (A)

Внутреннее сопротивление эквивалентного генератора: Rэ=Ux/Ik=2 (Oм).

Величину Rэ можно найти и другим способом. Оно равно входному сопротивлению двухполюсника при равенстве нулю всех его ЭДС. Если на рис. 1.21, а мысленно закоротить зажимы ЭДС Е1, то сопротивления R1 и R2 окажутся соединенными параллельно, и входное сопротивление цепи относительно зажимов m и n будет равно:

Ток в полученной неразветвленной цепи (рис. 1.20, б) определяется по закону Ома:

Подставляя в последнюю формулу требуемые значения сопротивления R3, вычисляем ток и строим график (рис. 1.22).

Данную задачу целесообразно решать именно методом эквивалентного генератора. Применение другого метода, например метода контурных токов, потребует решать систему уравнений столько раз, сколько значений тока необходимо найти. Здесь же всю цепь мы рассчитываем только два раза, определяя Еэ и Rэ, а многократно используем лишь одну простую формулу (1.13).

Уравнения четырехполюсника.

Четырехполюсником называется часть электрической цепи или схемы, содержащая два входных вывода (полюса) для подключения источника энергии и два выходных вывода для подключения нагрузки. К четырехполюсникам можно отнести различные по назначению технические устройства: двухпроводную линию, двухобмоточный трансформатор, фильтры частот, усилители сигналов и др.

Теория четырехполюсников устанавливает связь между режимными параметрами на входе (U1, I1) и режимными параметрами на его выходе (U2, I2), при этом процессы, происходящие внутри четырехполюсника, не рассматриваются. Таким образом, единая теория четырехполюсника позволяет анализировать различные по структуре и назначению электрические цепи, которые могут быть отнесены к классу четырехполюсников.

Если четырехполюсник не содержит внутри себя источников энергии, то он называется пассивным (обозначается буквой П), если внутри четырехполюсника имеются источники, то он называется активным(обозначается буквой А).

В настоящей главе анализируются пассивные линейные четырехполюсники. На электрических схемах четырехполюсники условно обозначаются прямоугольником с двумя парами выводов: 1 и 1' - входные выводы, 2 и 2' - выходные выводы (рис. 75.1). Соответственно напряжение и ток на входе индексируются цифрой 1 (U1, I1) , а на выходе - цифрой 2 (U2, I2).

Установим связь между параметрами режима входа (U1, I1) и выхода (U2, I2). Для этой цели согласно теореме о компенсации заменим нагрузку Z2 источником ЭДС Е2 = U2 = I₂Z₂ и найдем токи по методу наложения от каждого ис=точника в отдельности (рис. 75.2 а, б):

где Y₁₁, Y₂₂ – входные проводимости входа и выхода, Y₁₂ = Y₂₁ – взаимная проводимость между входом и выходом.

Выразим из полученных уравнений режимные параметры на входе:

С учетом принятых обозначений система основных уравнений четырехполюсника получит вид:

Уравнения четырехполюсника часто записывают в матричной форме:

Выразим соотношение между коэффициентами четырехполюсника:

A•D - B•C=1 – уравнение связи между коэффициентами. Уравнение связи показывает, что независимыми являются только три из четырех коэффициентов четырехполюсника.

Поменяем местами в схеме рис. 75.1 источник и приемник энергии. В новой схеме рис. 75.3 направления токов изменятся на противоположные.

Уравнения четырехполюсника с учетом изменения направлений токов примут вид:

Преобразуем полученную систему уравнений следующим образом. Умножим члены уравнения (1) на D, члены уравнения (2) на В и вычтем почленно из 1-го уравнения 2-ое. В результате получим:

Умножим члены уравнения (1) на С, члены уравнения (2) на А и вычтем из 1-го уравнения 2-ое. В результате получим:

Новая система уравнений четырехполюсника получила название формы В:

Четырехполюсник называется симметричным, если перемена местами входных и выходных выводов не влияет на режим остальной цепи, частью которой является четырёхполюсник. Для симметричного четырёхполюсника выполняются следующие условия:

Кроме названных форм уравнений четырехполюсника А и В применяются на практике еще четыре формы, а именно формы Z, Y, H и G. Структура этих уравнений приведена ниже:

Для уравнений формы Z, Y, H и G принята следующая ориентация токов и напряжений относительно выводов четырехполюсника (рис.75.3).

Соотношения между коэффициентами четырехполюсника различных форм приводятся в справочной литературе, однако их нетрудно получить, выполнив преобразование одной формы уравнений в другую. Например, пусть заданы коэффициенты формы А (А, В, С, D) и требуется определить коэффициенты формы Z(Z₁₁, Z₁₂, Z₂₁, Z₂₂). Для этого в уравнениях формы A изменим знак тока I2 и решим их относительно переменных U1 и U2:

Сравнивая полученные выражения с уравнениями четырехполюсника формы Z, находим соотношения между коэффициентами двух форм:

ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ ЧЕТЫРЁХПОЛЮСНИКОВ

ЛЕКЦИЯ 19

План лекции:

19.1. Основные определения и классификация четырёхполюсников

19.1. Основные определения и классификация четырёхполюсников

Электрическую цепь или её часть, рассматриваемые относительно двух пар выводов, называют четырёхполюсником (рис. 19.1).

Входную (первичную) пару выводов четырёхполюсника обозначают цифрами 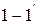, выходную (вторичную) – 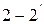. В качестве положительных принимают направления напряжений от верхних выводов к нижним, а токов – втекающими. В отдельных случаях положительными считают вытекающие токи. Вариант с положительными токам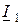и и 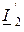называют прямой передаче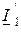й, и 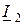– обратной, втекающими токам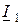и и 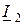– комбинированной. Сочетание токов 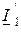и 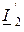специального названия не имеет и применяется редко.

В случае гармонических сигналов теория четырёхполюсников позволяет производить анализ и синтез цепей различных как по структуре и сложности, так и по принципу работы, не рассчитывая токи и напряжения всех реальных элементов внутри четырёхполюсников, что весьма упрощает и ускоряет получение результата. Например, сложную электрическую цепь можно представить в виде совокупности соединённых друг с другом исходных четырёхполюсников. Теория позволяет найти параметры эквивалентного обобщающего четырёхполюсника и рассчитать его входные и выходные сопротивления по известным параметрам исходного четырёхполюсника.

Различают линейные и нелинейные четырёхполюсники.

Четырёхполюсник называют линейным, если в его состав входят элементы только с линейными вольтамперными характеристиками. Четырёхполюс­ник называют нелинейным, если он содержит хотя бы один нелинейный элемент.

По наличию или отсутствию внутренних источников энергии четы­рёхполюсники делят на активные (автономные и неавтономные) и пассивные.

Активными автономныминазывают четырёхполюсники, содержащие независимые некомпенсированные источники эдс или тока. Независимыми называют источники, которые создают в ветвях четырёхполюсника токи и напряжения при отсутствии внешнего сигнала. Источник называют некомпенсированным, если между выводами четырёхполюсника существуют напряжения при отсутствии внешних цепей.

Активными неавтономными называют четырёхполюсники, содержащие зависимые источники эдс или тока как в сочетании с независимыми компенсированными источниками, так и без них. Генераторы эдс и тока, действие которых проявляется только при наличии внешних источников сигнала, называют зависимыми или неавтономными. К активным неавтономным относят, например, четырёхполюсники, содержащие транзисторы.

Четырёхполюсники называют пассивными, если они не содержат источников электрической энергии или являются линейными и содержат независимые компенсированные источники. При отсутствии внешних сигналов у пассивных четырёхполюсников напряжения между двумя любыми выводами равны нулю.

Четырёхполюсники делят на обратимые и необратимые.

Четырёхполюсник называют обратимымили взаимным, если для него выполняется принцип взаимности: отношение напряжения на входе к току на выходе не зависит от того, какая из двух пар выводов является входной и какая выходной.

Четырёхполюсники могут быть симметричными и несимметричными.

Четырёхполюсник называют симметричным, если перемена местами его входных и выходных зажимов не изменяет токов и напряжений во внешних цепях. Симметричные четырёхполюсники всегда обратимы. Электрическая симметрия не требует геометрической (топологической) симметрии его схемы. Однако если обратимый четырёхполюсник имеет топологическую симметрию, то одновременно обязательно существует электрическая симметрия.

Пассивные линейные четырёхполюсники всегда являются обратимыми.

Активные четырёхполюсники могут быть как обратимыми, так и необратимыми, причём активные несимметричные четырёхполюсники являются необратимыми.

Характеристики четырёхполюсника полностью описываются входными и выходными токами и напряжениями. Выбирая две любые из этих величин в качестве независимых, две оставшиеся можно выразить через них в виде системы из двух линейных алгебраических уравнений. Систему уравнений четырёхполюсника можно записать в виде одной из шести форм, что определяется выбранным сочетанием независимых величин.

1. ФормаY-параметров или, более кратко, форма .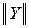

Здесь независимыми считают напряжения 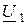и 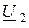, а зависимыми – ток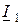и и :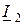

или в матричной записи

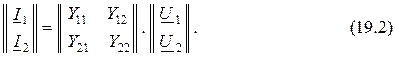
2. ФормаZ-параметров или :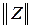

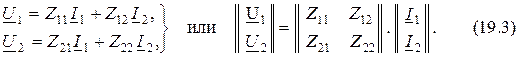
3. Форма A-параметров или :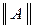

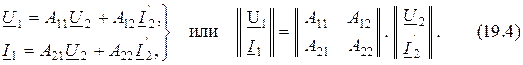
4. ФормаH-параметров или :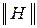

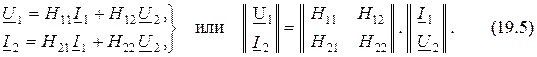
Если в качестве независимых выбраны 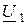и 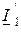, то система уравнений будет записана в 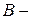параметрах, если независимыми являются 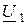и 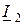, то – в 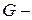параметрах.

Коэффициенты уравнений четырёхполюсника являются его первичными параметрами.

Выбор системы уравнений определяется в основном удобством экспериментального нахождения параметров. А именно, в качестве независимых токов и напряжений принимают те, которые для данного четырёхполюсника наиболее удобно изменять в процессе измерений, что однозначно определяет тип параметров и форму системы уравнений.

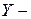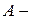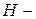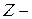Чаще других применяют , , и параметры. Например, свойства транзисторов в справочниках описывают через 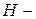параметры, так как наиболее удобно изменять ток базы 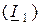и напряжение между коллектором и эмиттером .

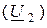Коэффициенты одной системы уравнений могут быть выражены через коэффициенты любой другой.

Пусть, например, известны 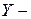параметры четырёхполюсника, а требуется найти его 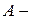параметры.

Для решения задачи преобразуем второе уравнение системы (19.1) к виду (19.4)

Подставим это уравнение в первое выражение из (19.1) и после преобразования получим

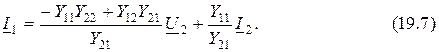
Сравнивая уравнения (19.6) и (19.7) с системой уравнений (19.4) и учитывая, что 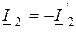, получаем

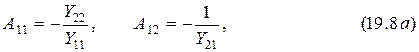
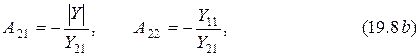
где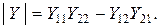

Поэтому достаточно знать параметры четырёхполюсника в какой-либо одной форме записи, чтобы получить их в любой другой. В литературе [1] и [3] имеются таблицы, облегчающие переход от одного вида параметров к другому.

К теме 1.4

Магнитный гистерезис

Магнитный гистерезис— явление зависимостивектора намагничиванияи вектора магнитной индукции в веществе не только от приложенного внешнего поля, но и от истории данного образца. Магнитный гистерезис обычно проявляется вферромагнетиках—Fe,Co,Niи сплавах на их основе. Именно магнитным гистерезисом объясняется существованиепостоянных магнитов.

Теория явления гистерезиса учитывает конкретную магнитную доменную структуру образца и её изменения в ходе намагничивания и перемагничивания. Эти изменения обусловлены смещением доменных границ и ростом одних доменов за счёт других, а также вращением вектора намагниченности в доменах под действием внешнего магнитного поля. При полной ориентации всех доменов в направлении внешнего поля (ферромагнетик становится «однодоменным») достигается состояние насыщения. При выключении внешнего поля происходит некоторое уменьшение намагниченности вследствие теплового движения в кристалле, однако ферромагнетик остается намагниченным, так как при невысоких температурах энергия теплового движения сравнительно невелика и ее недостаточно для полной разориентации доменов.

Эти процессы требуют больших энергетических затрат и являются нелинейными. Кривая размагничивания ферромагнетика не совпадает с кривой намагничивания. Изменение намагниченности ферромагнетика (и индукции поля в нем) запаздывает по отношению к изменению напряженности внешнего поля. Это явление называетсягистерезисом.При уменьшении напряженности внешнего поля до нуля, индукция поля в магнетике не равна нулю, ее величина называетсяостаточной индукциейВ_о. Чтобы полностью размагнитить магнетик, надо изменить направление внешнего поля на противоположное, и увеличивать его. При некотором значении напряженности «обратного» поля Н_с, называемомкоэрцитивной силой,магнетик полностью размагничивается. Замкнутая кривая, отражающая процесс перемагничивания ферромагнетиков, называетсяпетлей гистерезиса(рис.1).

Рис.1. Петля гистерезиса

На данном графике точки В и С характеризуют состояние насыщения. Величина остаточной индукции характеризуется отрезком B₀.

Коэрцитивная сила определяется точкой пересечения петли гистерезиса с осью напряженности магнитного поля. По величине коэрцитивной силы ферромагнетики разделяются на мягкие и жесткие магнитные материалы.

Жесткие ферромагнетики используются для постоянных магнитов, они имеют большую остаточную намагниченность и широкую петлю гистерезиса.

Мягкие ферромагнетики применяются в приборах и установках, работающих с переменными электромагнитными полями, где требуется частое перемагничивание при минимальных энергетических потерях (например, в сердечниках трансформаторов). Для них характерна небольшая остаточная намагниченность и узкая петля гистерезиса.

Описание установки

Опытная установка состоит из модуля ФПЭ-07, генератора сигналов ФГ-100 и осциллографа. Модуль содержит тороидальный трансформатор с исследуемым ферромагнитным сердечником в форме кольца, резисторы R_1, R₂и конденсатор С. С выхода генератора переменное напряжение через резисторR₁ подается на первичную обмотку трансформатора, а затем - на вход «Х» осциллографа. Напряженность магнитного поля, создаваемого током первичной обмотки, пропорциональна напряжению на нейU_x. С вторичной обмотки трансформатора через цепь, содержащую резисторR₂и конденсатор С, сигнал подается на вход «Y» осциллографа. Индукция магнитного поля, возникающего в ферромагнитном сердечнике, пропорциональна напряжению на вторичной обмотке трансформатораU_y.

К теме 1.5

ТАБЛИЦА № 1

МАТЕРИАЛ	Удельное сопротивление	Удельная проводимость
Серебро	0,016	62,5
Медь	0,01786
Золото	0,024	41,6
Алюминий	0,0286
Вольфрам	0,055
Латунь	0.071	14,1
Железо	0,1 - 0,15	10 - 7
Свинец	0,21	4,8
Платиноиридиевый сплав	0,25
Никелин	0,43	2,3
Константан	0,5
Хромоникель	1,1	0,91
Графит		0,08
Уголь		0,025
Твердые изоляторы	От 10(в степени 6) и выше	10(в степени минус 6)
Фарфор	10(в степени 19)	10(в степени минус 19)
Эбонит	10(в степени 20)	10(в степени минус 20)
Жидкие изоляторы	От 10(в степени 10) и выше	10(в степени минус 10)
Газообразные	От 10(в степени 14) и выше	10(в степени минус 14)

Из таблицы можно видеть, что самыми проводящими материалами являются – серебро, золото, медь и алюминий. В силу высокой стоимости серебро и золото применяется только в высокотехнологичных схемах. А медь и алюминий получили широчайшее применение в качестве проводников.
Еще видно, что нет абсолютно проводящих материалов, поэтому при расчетах всегда надо учитывать, что в проводах теряется ток и падает напряжение.
Есть еще одна, довольно большая и "интересная" группа материалов – полупроводники. Проводимость этих материалов изменяется в зависимости от условий окружающей среды. Полупроводники начинают лучше или, наоборот, хуже проводить ток, если их подогреть/охладить, или осветить, или согнуть, или, например, ударить током.

К теме 1.6

34.Условие и способы получения резонанса. Резонансная частота

Явление резонанса. Электрическая цепь, содержащая индуктивность и емкость, может служить колебательным контуром, где возникает процесс колебаний электрической энергии, переходящей из индуктивности в емкость и обратно. В идеальном колебательном контуре эти колебания будут незатухающими. При подсоединении колебательного контура к источнику переменного тока угловая частота источника ? может оказаться равной угловой частоте ?0, с которой происходят колебания электрической энергии в контуре. В этом случае имеет место явление резонанса, т. е. совпадения частоты свободных колебаний ?0, возникающих в какой-либо физической системе, с частотой вынужденных колебаний ?, сообщаемых этой системе внешними силами.

Резонанс в электрической цепи можно получить тремя способами: изменяя угловую частоту ? источника переменного тока, индуктивность L или емкость С. Различают резонанс при последовательном соединении L и С — резонанс напряжений и при параллельном их соединении — резонанс токов. Угловая частота ?0, при которой наступает резонанс, называется резонансной, или собственной частотой колебаний резонансного контура.

35. Резонанс в последовательном колебательном контуре. Добротность, векторная диаграмма. Характеристическое сопротивление, затухание контура.

Резонанс напряжений – явление, при котором цепь содержащая активные и реактивные сопротивления, будет только активное сопротивление (XL - XC = 0). При этом ток в цепи совпадает по фазе с напряжением. Условие возникновение резонанса напряжений – равенство нулю реактивного сопротивления.

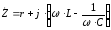
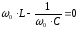
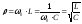- характеристическое сопротивление контура.

Таким образом:

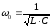–резонансная частота

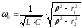-резонансная для парралельного

При резонансе напряжений ток максимален, так как сопротивление минимально, а

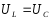
и таким образом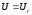

Добротностью контура называется отношение м