Вопрос – 2. Симметрия и структура кристаллов. Индексы Миллера.

Кристаллы – это тела, в которых составляющие их частицы (атомы, молекулы) образуют упорядоченную периодическую структуру. Вследствие закономерности в своем строении кристаллы однородны и анизотропны. Идеальный кристалл можно построить путем бесконечного повторения в пространстве его структурной единицы, называемой элементарной ячейкой, выбор которой неоднозначен. В общем случае элементарная ячейка имеет форму параллелепипеда (рис. 1) и характеризуется 6 параметрами: длинами ребер a, b, c и углами между ними α, β, γ. В элементарной ячейке может содержаться один атом, тогда ее называют примитивной, или больше одного, тогда это ячейка с базисом.   Рис.1. Элементарная ячейка.     При описании симметрии любого кристалла используется фундаментальное понятие решетки Бравэ, которое характеризует периодическую структуру, образуемую повторяющимися элементами кристалла. Решеткой Бравэ называется множество точек в пространстве с радиус-векторами Rn = n1a1 +n2a2 +n3a3, где a1, a2, a3 – тройка линейно независимых векторов, называемых основными векторами решетки, 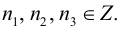В зависимости от отношения величин и взаимной ориентации основных трансляций a1, a2, a3 получаются решетки, отличающиеся друг от друга по своей симметрии. Математически доказано, что всего существует 14 типов таких различных по симметрии трансляционных решеток. Следует отличать понятия кристаллическая структура и кристаллическая решетка. Структура кристалла – это физическая реальность, характерное для данного твердого тела распределение частиц в пространстве. Совокупность атомов, содержащихся внутри объема элементарной ячейки, называют базисом. Пространственная решетка – это математическая абстракция, используемая для описания симметрийных свойств кристалла. Справедливо определение:     Решетка + Базис = Кристаллическая структура.   Наряду с трансляционной симметрией, связанной с переносом тела как целого, кристаллы обладают также точечной симметрией. Точечной группой симметрии называется множество точечных операций симметрии, совмещающих решетку саму с собой, к ним относят отражения в зеркальных плоскостях и повороты. Совокупность элементов точечной и трансляционной групп симметрии образует пространственную группу симметрии кристалла. В кристаллографии существуют понятия кристаллографических плоскостей и направлений. Расположение атомных плоскостей имеет значение, например, при описании дифракции рентгеновских лучей в кристалле. Кристаллографическая плоскость (узловая плоскость) – это плоскость, проходящая не менее чем через три узла решетки, не лежащие на одной прямой. Система параллельных узловых плоскостей, расположенных на одинаковом межплоскостном расстоянии d друг от друга, образует семейство плоскостей. Любая пространственная решетка может быть представлена семействами узловых плоскостей неограниченным числом способов. Семейство параллельных узловых плоскостей характеризуется тремя взаимно простыми числами (hkl) – индексами Миллера, которые удовлетворяют соотношению: (a/x):(b/y):(c/z) = h:k:l, где x, y, z – длины отрезков, отсекаемых плоскостью (hkl), ближайшей к началу координат, на осях, параллельных ребрам элементарной ячейки. Кристаллографическое направление (узловая прямая) – это прямая, проходящей не менее чем через два узла решетки. Направления в кристаллах принято характеризовать символом узла, через который проходит данная узловая прямая и ближайшего к узлу, в котором находится начало системы координат: [mnp]. При анализе многих явлений в физике твердого тела играет важную роль так называемая обратная решетка. Основные векторы обратной решетки biопределяются соотношениями (ai,bk) = 2πδik (i, k = 1, 2, 3), где ai – основные векторы прямой решетки. Таким образом, обратная решетка – это множество точек с радиус-векторами Gn = n1b1+n2b2+n3b3, где ni – целые числа. В отличие от реальной кристаллической решетки, никаких частиц в узлах обратной решетки реально не существует, она является удобной абстракцией, позволяющей математически просто описывать определенные свойства кристалла.

Вопрос – 3 Дифракционные методы определения параметров кристаллов.

Сведения о структуре кристаллов можно получить из изучения внешней морфологии (строения) образца. С помощью оптического прибора гониометра определяют углы между плоскостями кристалла. По отражению света от поверхности образца можно определить кристаллографическую ориентацию монокристалла с известной структурой (например, Si или Ge).

Однако для исследования внутренней структуры кристалла используют различные дифракционные методы, для этого необходимо излучение, сравнимое с межатомными расстояниями (порядка 0,1 нм).

а) Электромагнитное рентгеновское излучение (оценки для l = 1 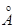= 0,1 нм)

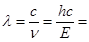0,1 нм (2.4)

Для получения такой длины волны энергия ускорения электронов должна быть Е = 12 кэВ.

Рентгеновские лучи хорошо проникают в кристалл, но не годны для исследования легких атомов (так как рассеиваются электронными оболочками, которые у легких атомов содержат малое количество электронов).

б) Ускоренные электроны как квантовые частицы:

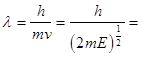0,1 нм (2.5)

Для получения такой длины волныпотребуется ускоряющая энергия, равная Е ~ 150 эВ; v ~ 7×10⁶ м/с.

Поскольку электроны заряжены и легко поглощаются поверхностью, они хороши для исследования тонких пленок. За счет взаимодействия с заряженными ядрами обладают большой интенсивностью дифракции (в 10⁶ раз сильнее, чем дифракция рентгеновских лучей).

в) Поток нейтронов

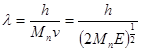(2.6)

Для получения излучения с длиной волны l ~ 0,1 нмнеобходима энергия Е ~ 0,08 эВ; v ~ 4×10³ м/с.

Нейтроны нейтральны, рассеиваются на ядрах любых атомов, в том числе на легких. Глубоко проникают в объем кристалла.

Используя любой вид излучения, можно получить дифракционную картину на трехмерной решетке, которой является кристалл.

Условие дифракции Брэгга. Рентгеновские лучи отражаются от межатомных плоскостей, приобретают разность хода и интерферируют (рис. 2.7). Если разность хода D равна целому числу l, то наблюдается интерференционный максимум. Условие Вульфа–Брэгга:

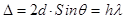, (2.7)

где h – целое число (h = 1, 2, ...).

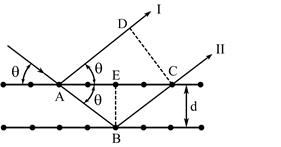
Рис. 2.7. Дифракция рентгеновских лучей в кристалле

В соответствии с рис. 2.7.

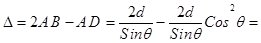
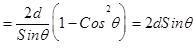(2.8)

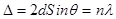(2.9)

Узость рентгеновского луча, обусловленная малой диафрагмой, и большой размер зерна фотоэмульсии пленки, на которой наблюдаются условия дифракции, позволяют отказаться от фокусировки.

Измерив угол максимального отражения q, можно определить d для разных плоскостей, а по ним найти h k l:

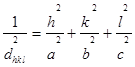. (2.10)

Для куба a = b = c:

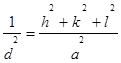. (2.11)