Уравнение первого закона термодинамики для потока газа

Ранее было показано, что dq = di – vdP. Т.к. 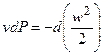, то

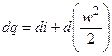. (6.8)

При адиабатном течении газа dq = 0, и для этого случая:

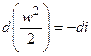, (6.9)

Если газ при течении по каналу совершает техническую работу l_тех, то уравнение первого закона имеет вид:

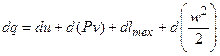, или

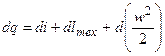. (6.10)

При адиабатном течении газа dq = 0, отсюда:

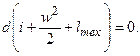(6.11)

После интегрирования:

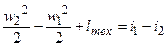. (6.12)

Располагаемая работа газа в потоке

Ранее было показано, l₀ – располагаемая работа равна: l₀ = -vdP, но 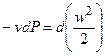, т.е. располагаемая работа l₀при течении газа равна его кинетической энергии:

l₀ = 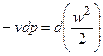. (6.13)

Из уравнения видно, что при обратимом процессе увеличение скорости w связано с уменьшением давления, и наоборот, уменьшение скорости сопровождается повышением давления.

Сопла – это каналы, в которых происходит расширение газа с уменьшением давления (dP< 0) и увеличением скорости (dw > 0).

Диффузоры- это каналы, в которых происходит сжатие газа с увеличением давления (dP > 0) и уменьшением скорости (d w < 0).

Как известно, располагаемая работа l₀ зависит от вида процесса. Причем располагаемая работа может быть больше, меньше работы расширения или равна ей.

Для адиабатного процесса расширения газа l₀ = kl, или

.

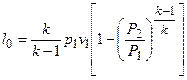Для адиабатного течения газа располагаемая работа может быть определена через энтальпию. Т.к.

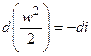, а

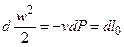, то 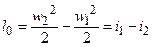. (6.14)

Уравнение неразрывности

Рассмотрим движение потока газа через трубу переменного сечения (рис. 6.3). Если течение газа установившееся, то через любое произвольное поперечное сечение трубы в единицу времени протекает одна и та же масса газа.

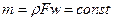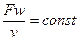, или и 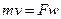, где (6.15)

r - плотность; F – площадь поперечного сечения трубы; w - скорость; v – удельный объем.

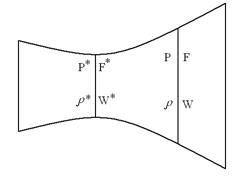
Рисунок 6.3 - К выводу уравнения неразрывности

Уравнение 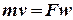называется уравнением неразрывности или сплошностипотока.

При течении сжимаемого газа профиль сопла при данном расходе газа m = const будет зависеть не только от характера изменения скорости w, но и от плотности r (удельного объема v), который изменяется по закону адиабаты.

Логарифмируя и дифференцируя уравнение сплошности (при m = const) получаем:

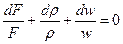
Это уравнение неразрывности в дифференциальной форме, которое с помощью уравнения Бернулли может быть приведено к форме

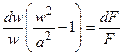, или 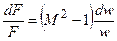, (6.16)

где а – местная скорость звука.

Отношение скорости газа w к местной скорости звука а в этом же сечении канала

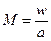
называют числом Маха. Различают дозвуковую и сверхзвуковую скорости газа. При М > 1- сверхзвуковая, при М < 1 - дозвуковая скорости течения.

Скорость истечения

Чтобы найти скорость истечения газа через сопло, нужно проинтегрировать уравнение:

; ,

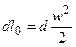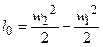где w ₁ и w ₂ – значения скорости в конце и начале процесса.

Для случаев, когда , w ₂ >> w ₁, то членом w₁ можно пренебречь, получаем:

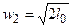, (6.17)

но т.к. l₀ связано с параметрами 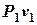, можно записать:

,

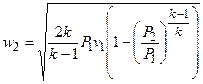или

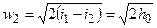(6.18)

При истечении газа в вакуум (P₂ = 0) скорость истечения будет максимальная.

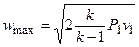. (6.19)