Расчет основных параметров влажного воздуха

Основными характеристиками влажного воздуха являются абсолютная и относительная влажность, влагосодержание и степень насыщения.

Абсолютной влажностью воздуханазывается количество водяного пара (кг), содержащегося в 1м³ влажного воздуха. Абсолютная влажность может быть выражена в виде плотности пара r_п в смеси при своем парциальном давлении Р_п и температуре смеси:

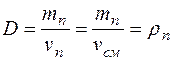(5.42)

Относительной влажностью воздуханазывается отношение действительной абсолютной влажности воздуха r_п к максимально возможной абсолютной влажности r_s при той же температуре:

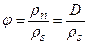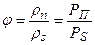, или . (5.43)

Точка росы характеризуется конденсацией части пара (образование капелек жидкости), содержащегося во влажном воздухе.

Влагосодержание d оценивается отношением количества 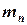водяного пара (в кг), содержащегося в сухом воздухе, к количеству 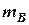воздуха:

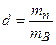. (5.44)

Так как объем пара 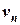, содержащегося в воздухе, и объем воздуха 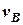равны объему смеси 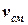, то выражение (8.4) можно представить в виде:

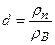. (5.45)

Основные параметры влажного воздуха (плотность, газовая постоянная и др.) могут быть подсчитаны по формулам смеси идеальных газов.

5.11.3 di-диаграмма влажного воздуха

di-диаграмма влажного воздуха предложена в 1918 г. Л.К. Рамзиным и применяется для определения параметров влажного воздуха при расчетах процессов сушки, вентиляции и отопления. При построенииdi-диаграммы используются косоугольные координаты, при которых прямые i=const проводятся под углом 135° к оси ординат (рис. 8.1). Ось влагосодержания dусловно проводится к оси ординат под углом 90°.

На диаграмму наносят сетку изотерм. На каждой изотерме находят точки с одинаковыми значениями 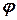, соединив которые, получают сетку кривых относительных влажностей воздуха 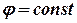. Кривая 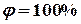- геометрическое место точек росы и является пограничной кривой, разделяющей область ненасыщенного влажного воздуха (сверху) и область тумана (снизу), в которой влага частично находится в капельном состоянии.

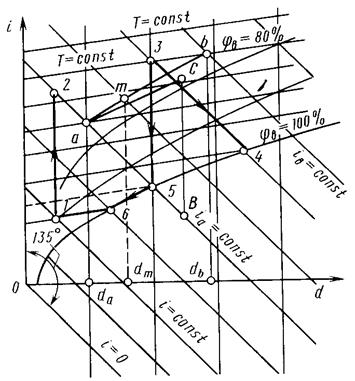
Рисунок 5.12 - di-диаграмма влажного воздуха (диаграмма Рамзина)

При помощи di-диаграммы можно проводить следующие расчеты:

· Подогрев и охлаждение влажного воздуха, находящегося в калорифере, происходит при постоянном влагосодержании – соответственно вертикали 1-2 и 3-5. По мере охлаждения в точке 5 ранее перегретый пар становится сухим; при дальнейшем охлаждении часть пара конденсируется, и влагосодержание воздуха уменьшается. Процесс 5-6 происходит по кривой 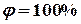. Количество сконденсировавшейся влаги равно: .

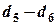· Процесс испарения 3-4 определяется при условии 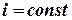. С испарением влаги встречаются при сушке материалов перегретым воздухом. Испарение влаги происходит за счет теплоты воздуха. При этом влагосодержание воздуха увеличивается, а температура понижается. Энтальпия остается постоянной, т.к. теплота, затраченная на испарение влаги, возвращается обратно во влажный воздух с испарившейся влагой.

· В результате смешения двух потоков влажного воздуха с параметрами, характеризуемыми точкам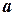и и 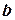, получаем поток влажного воздуха с параметрами, характеризуемыми точкой 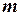. Для этого соединим точк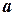и и 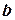прямой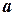 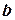, и при помощи массовых долей смешиваемых потоков, т.е. точка 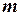делит прямую смешения в отношении 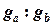. Координаты (влагосодержание и энтальпия) точки 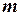определяются по формулам:

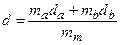; (5.46)

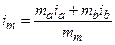, (5.47)

где 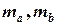- массы потоков; 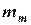- масса потока после смешения.

Литература: [2], с. 49-56; [5], с. 20-25; [6], с. 48-70; [8], с. 346-352, 568-580.

Вопросы для самоконтроля

1. Изобразите процесс парообразования на vP- и sT-диаграммах.

2. Какой пар называется влажным? Сухим? Перегретым?

3. Какой пар называется насыщенным? Чему равна его степень сухости?

4. Покажите на is-диаграмме критическую точку, - чем она характеризуется?

5. Почему на теплоэлектростанциях с повышением давления перегретого пара возникает экономия топлива?

6. Какими параметрами можно охарактеризовать состояние влажного, сухого и перегретого пара?

7. Что такое скрытая теплота парообразования? Покажите ее на sT- и is-диаграммах для какого-либо одного давления.

8. Дайте определение влажного воздуха.

9. Что такое абсолютная влажность воздуха? В каких единицах она измеряется?

10.Что такое влагосодержание воздуха? В каких единицах оно измеряется?

11.Что такое относительная влажность воздуха?

12.Что такое точка росы?

13.В каких пределах может измеряться влагосодержание?

14.Как изменяется влагосодержание воздуха при его охлаждении?

15.Как изменяется влагосодержание при нагреве воздуха?

16.Покажите на id-диаграмме, как определяется парциальное давление водяных паров.

17.Какие процессы можно построить на id-диаграмме влажного воздуха?

6 Течение, истечение и нагнетание газов и паров

Процессы течения газов в каналах различной формы встречаются при проектировании различных технологических устройств. Расчет таких процессов базируется на основных уравнениях газовой динамики. Применение этих уравнений и остальных законов термодинамики позволяет определить значение скоростей и остальных параметров потока в любом сечении канала. В настоящей лекции рассматриваются процессы течения газа в рамках установившейся и одномерной модели потока.

Установившееся (стационарное) течение – это течение, при котором в каждой точке пространства параметры потока не изменяются во времени. Одномерное течение – течение, при котором параметры газа изменяются только в одном направлении, т.е. в каждом поперечном сечении потока все параметры, а также скорость являются постоянными. Однако известно, что вследствие вязкости газа скорость его в пределах поперечного сечения несколько изменяется (рис. 6.1). Максимальная скорость имеет место на оси канала, у стенки скорость газа равна нулю. При допущении одномерности течения газа его действительные параметры в каждом поперечном сечении заменяются их усредненными значениями, что упрощает вид основных уравнений газовой динамики.

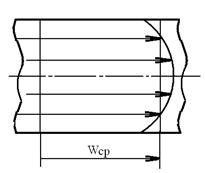
Рисунок 6.1 - Эпюра распределения скоростей в канале

Если течение газа происходит без теплообмена с окружающей средой и без трения, то такое движение называется адиабатным течением.

При исследовании одномерного течения определяют изменение давления и плотности 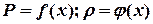по сечениям вдоль потока. Для описания течения газов обычно применяют систему уравнений, включающих уравнения движения, неразрывности, первого закона термодинамики и состояния газа, движение которого изучается.

Уравнения движения

Рассмотрим движение потока идеального газа через трубу переменного сечения (рис. 6.2).

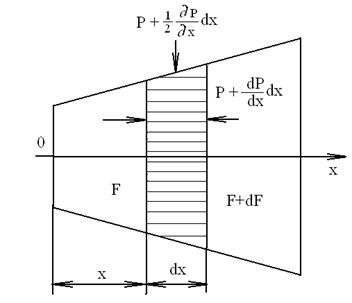
Рисунок 6.2 - К выводу уравнения движения

Выделим в произвольный момент времени t объем газа между двумя близкими сечениями трубы F и F+dF, находящимися на расстоянии dх. Если пренебречь силой вязкости, то объем газа движется в направлении оси х со скоростью w под действием поверхностных сил от давления. Согласно второму закону механики, уравнение движения газа, находящегося в объеме Fdх, имеет вид:

,

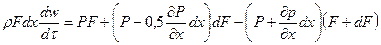или:

.

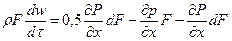С точностью до малых первого порядка:

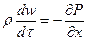, (6.1)

где давление P = f(x,t); плотность r = j(x,t) и скорость w = w(x,t). В последнем уравнении 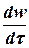- полная производная, то есть:

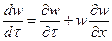, (6.2)

отсюда

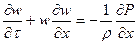. (6.3)

Для установившегося движения 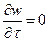, и поэтому

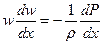, или 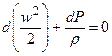, (6.4)

где Р, r, w являются функциями только координаты х. Последнее уравнение называется уравнением Бернулли в дифференциальной форме. Если r = const, то после интегрирования получим:

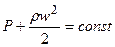, (6.5)

где 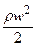- скоростной напор.

Если плотность r зависит от давления r = r(Р), то уравнение Бернулли можно записать в интегральной форме:

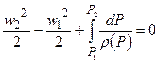. (6.6)

Для вычисления интеграла давления

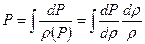
необходимо знать зависимость r = r(Р) или Р = Р(r).

С учетом соотношения 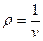получаем:

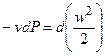. (6.7)