Аналитическое выражение II закона термодинамики.

Для обратимого цикла Карно имеем:

,

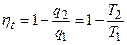тогда 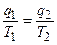или .

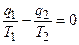Если учесть в этом соотношении, чтоq₁ >0 (теплота подводится к рабочему телу) и q₂<0 (теплота отводится от рабочего тела), то

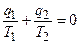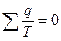или (4.6)

Отношение подводимой или отводимой теплоты к соответствующей абсолютной температуре называется приведенной теплотой. Выражение (6.6) показывает, что алгебраическая сумма приведенных теплот для обратимого цикла Карно равна нулю, т.е.

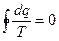. (4.7)

Отношение 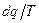считают полным дифференциалом функции состояния 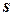, называемой энтропией. Т.к. dq = Tds, то

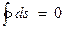(4.8)

Таким образом, алгебраическая сумма приведенных теплот для любого обратимого цикла равна нулю. Энтропия рабочего тела в результате совершения произвольного обратимого цикла не изменяется.

Уравнение (4.8), выведенное Клаузиусом в 1854 году, представляет собой аналитическое выражение второго закона термодинамики для произвольного обратимого цикла и называется первым интегралом Клаузиуса.

В цикле с необратимыми процессами при прочих равных условиях работа, совершаемая рабочим телом меньше, чем в цикле с обратимым процессом, и при одинаковх температурах источника теплоты и холодильника

h _tнеобр<h_t.

Поэтому при наличии в цикле необратимых процессов:

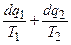<0 (4.9)

или после интегрирования по контуру

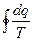<0(4.10)

Это неравенство представляет собой аналитическое выражение второго закона термодинамики для произвольного необратимого цикла и называется вторым интегралом Клаузиуса.

Объединяя (4.7) и (4.10), можно записать одно уравнение второго закона термодинамики для обратимых (=) и необратимых (<) циклов:

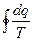£0 (4.11)

Энтропия есть функция состояния рабочего тела, поэтому изменение энтропии как для обратимого, так и необратимого процессов будет одним и тем же.

Для элементарного необратимого процесса

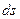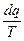> (4.12)

В общем виде для любого процесса изменение энтропии удовлетворяет соотношению

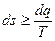, (4.13)

где dq - количество теплоты, полученное телом от источника теплоты;

Т- абсолютная температура источника теплоты.

Знак равенства относится к обратимым, знак неравенства - к необратимым процессам.

Следует различать понятия энтропия телаи энтропия системы.

Энтропия не является функцией состояния системы, состоящей из нескольких тел (рабочее тело, холодильники и источники теплоты), каждое из которых характеризуется своими параметрами. Поэтому на изменение энтропии системы влияет характер процесса теплообмена между рабочим телом и источником теплоты. При протекании обратимых процессов энтропия системы остается постоянной; при необратимых процессах энтропия системы возрастает.

Если в адиабатной изолированной системе протекают только обратимые процессы, то

ds = dq/T,

для адиабатной системы это уравнение принимает вид: dq = Tds = 0

Так как Т ¹ 0, то для всей системы ds = 0 и s = const.

Таким образом, если в изолированной адиабатной системе протекают только обратимые процессы, то энтропия всей системы остается величиной постоянной.

Для адиабатной системы при наличии в ней необратимых процессов:

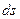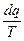> .(4.14)

Т.к.dq = 0, то для адиабатной изолированной системы ds ³ 0, т.е. происходит увеличение энтропии.

В термодинамике большое значение имеет понятие работы, которую совершает система при изменении своего состояния и условий, при которых получается максимальная работа.

Максимальная работоспособность системы, получаемая в обратимом цикле Карно в температурном интервале от 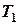до 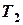, называется эксергией (ex).

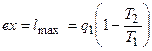. (4.15)

Работа необратимого цикла Карно, в котором теплота 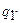передается рабочему телу при температуре 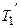ниже температуры нагревателя :

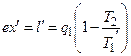. (4.16)

Потеря работы :

. (4.17)

Эксергия является обобщенной качественной и количественной характеристикой для потока теплоты и потока вещества, зависящей одновременно от параметров системы и окружающей среды. В отличие от энергии в реальных процессах, эксергия количественно не сохраняется. Всякая необратимость в системе приводит к уменьшению работоспособности, т.е. к потерям энергии. Уменьшение работы ведет к увеличению энтропии :

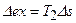. (4.18)

Уравнение (4.18) называют уравнением Гюи-Стодолы.