Вычисление энтропии идеального газа
Формулы для вычисления изменения энтропии идеального газа могут быть получены из уравнения первого закона термодинамики:

В процессе при v=const , в котором тело не совершает внешней работы

Или, заменив Р на  из уравнения Клапейрона, получим
из уравнения Клапейрона, получим

Разделив обе части последнего уравнения на Т, имеем:

Так как  , то
, то
 (3.1)
(3.1)
Интегрируя (3.1) при cv=const, найдем

Таким образом, получено уравнение для вычисления энтропии как функции температуры и удельного объема 
Для получения изменения энтропии как функции температуры и давления  следует из уравнения (5.1) исключить
следует из уравнения (5.1) исключить  .
.
Из уравнения Клапейрона после дифференцирования получаем
 ;
;
 ;
;
 .
.
Так как  ,то
,то

Или, разделив на  :
:
 .
.
Подставляя из последнего выражения  в уравнение (5.1) и учитывая, что из уравнения Майера
в уравнение (5.1) и учитывая, что из уравнения Майера  , найдем:
, найдем:
 . (3.2)
. (3.2)
Интегрируя последнее уравнение при  const, получаем выражение для определения изменения энтропии как функции температуры и давления
const, получаем выражение для определения изменения энтропии как функции температуры и давления
 .
.
Для получения изменения энтропии как функции давления и удельного объема следует из уравнения (5.2) исключить  .
.
 ;
;
 ;
;
 (3.3)
(3.3)
Изохорный процесс
Термодинамический процесс, протекающий при  =const или
=const или  , называется изохорным, а кривая процесса – изохорой.
, называется изохорным, а кривая процесса – изохорой.
Таблица 3.2 – Исследование изохорного процесса
| Метод исследования | Формулы |
1. Уравнение кривой процесса в  - диаграмме - диаграмме |  , ,  |
2. График процесса в  и и 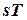 - координатах - координатах | |
Изохора 1-2 – вертикальная прямая, параллельная оси  В процессе 1-2 теплота подводится к газу, давление повышается. В обратном процессе 2-1 теплота от газа отводится, давление понижается. В процессе 1-2 теплота подводится к газу, давление повышается. В обратном процессе 2-1 теплота от газа отводится, давление понижается. |  |
Pис. 3.1 - Изохорный процесс в  координатах координатах |
Продолжение таблицы 3.2
Площадь под изохорным процессом в 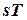 -диаграмме (пл. 1234) численно равна количеству теплоты, которая расходуется на изменение внутренней энергии рабочего тела, а подкасательная к кривой в любой точке дает значение истинной теплоемкости cv. Чем больше объем газа, тем дальше находится изохора от оси координат. -диаграмме (пл. 1234) численно равна количеству теплоты, которая расходуется на изменение внутренней энергии рабочего тела, а подкасательная к кривой в любой точке дает значение истинной теплоемкости cv. Чем больше объем газа, тем дальше находится изохора от оси координат. |  |
Pис. 3.2 - Изохорный процесс в 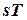 - координатах - координатах | |
| 3. Изохорный процесс описывается уравнением состояния в виде: При изохорном процессе давление газа пропорционально абсолютной температуре (закон Шарля): |  |
| 4. Изменение внутренней энергии газа при постоянной теплоемкости |  |
5. Внешняя работа газа при  =constравна нулю, так как =constравна нулю, так как  =0. =0. |   |
| 6. Удельная располагаемая работа в изохорном процессе: |  |
| 7. Вся подведенная теплота в рассматриваемом процессе идет на изменение внутренней энергии рабочего тела. |  |
| 8. Изменение энтальпии в процессе: |  , , |
| 9. Изменение удельной энтропии в обратимом изохорном процессе определяется по формуле: |   . .  . . |
Продолжение таблицы 3.2
10. Так как в изохорном процессе  , то доля теплоты, расходуемая на изменение внутренней энергии, равна: , то доля теплоты, расходуемая на изменение внутренней энергии, равна: |  |
| 11. Доля теплоты, расходуемая на совершение работы |  |
Изобарный процесс
Процесс, протекающий при постоянном давлении  или
или  , называется изобарным, а кривая процесса – изобарой.
, называется изобарным, а кривая процесса – изобарой.
Таблица 3.3 – Исследование изобарного процесса
| Метод исследования | Формулы |
1. Уравнение кривой процесса в  - диаграмме - диаграмме |  , , 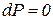 , , |
2. График процесса в  и и 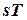 - координатах - координатах |  |
Pисунок 3.3. - Изобарный процесс в  координатах координатах | |
3. Площадь под изохорным процессом в 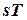 -диаграмме (пл. 1234) численно равна количеству теплоты, которая расходуется на изменение энтльпии рабочего тела, а подкасательная к кривой в любой точке дает значение истинной теплоемкости cv. Изобарный процесс на -диаграмме (пл. 1234) численно равна количеству теплоты, которая расходуется на изменение энтльпии рабочего тела, а подкасательная к кривой в любой точке дает значение истинной теплоемкости cv. Изобарный процесс на 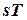 -диаграмме протекает более полого, чем изохорный процесс того же газа. -диаграмме протекает более полого, чем изохорный процесс того же газа. |  |
Рисунок 3.4 - Изохорный процесс в 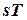 - координатах - координатах | |
| 4. Изобарный процесс описывается уравнением состояния в виде: |  |
Продолжение таблицы 3.3
| 5. Изменение внутренней энергии газа при постоянной теплоемкости |  |
6. Удельная работа изменения объема Или с учетом уравнения состояния  |    |
| 7. Удельная располагаемая работа в изобарном процессе: |  , т.к. , т.к.  |
| 8. Основное уравнение первого закона термодинамики для изобарного процесса имеет вид: |  |
| 9. Удельное количество теплоты, сообщенное телу в изобарном процессе, равно разности энтальпий конечного и начального состояний тела: |  |
| 10. Изменение удельной энтропии в обратимом изобарном процессе определяется по формулам: |     |
11. Доля теплоты, расходуемая на изменение внутренней энергии в изобарном процессе: Для двухатомных газов  , тогда , тогда |   |
| 12. Доля теплоты, расходуемая на совершение работы Для двухатомных газов |   |
Изотермический процесс
Изотермический процесс протекает в условиях постоянной температуры, т.е. при  или
или  .
.
Таблица 3.4 – Исследование изотермического процесса
| Метод исследования | Формулы | ||
1. Уравнение кривой процесса в  - диаграмме - диаграмме |  ; ;  . . | ||
2. График процесса в  и и 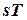 - координатах - координатах | |||
В  диаграмме изотермический процесс представляет собой равнобокую (равностороннюю) гиперболу. Чем выше температура диаграмме изотермический процесс представляет собой равнобокую (равностороннюю) гиперболу. Чем выше температура  , тем выше в , тем выше в  диаграмме располагается изотерма. диаграмме располагается изотерма. |  |  | |
Pисунок 3.5 - Изотермический процесс в  координатах координатах | Pисунок 3.6 - Изотермический процесс в 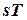 - координатах - координатах | ||
| 3. Изотермический процесс описывается уравнением состояния в виде: |  | ||
4. Изменение внутренней энергии равно нулю, т.е.  |  | ||
| 5. Удельная работа в изотермическом процессе: |     | ||
| 6. Удельная располагаемая работа Следовательно, в изотермическом процессе для идеального газа располагаемая работа l0 равна работе процесса l. |   | ||
| 7. Уравнение первого закона термодинамики для изотермического процесса имеет вид: |  или или  | ||
| 8. При T = const dT = 0: |  ,т.е. ,т.е.   |
Прдолжение таблицы 3.4
| 9.Изменение удельной энтропии: |   |
| 10.Доля теплоты, расходуемая на изменение внутренней энергии в изотермическом процессе: |  |
| 11. Доля теплоты, расходуемая на совершение работы |  |
Адиабатный процесс
Адиабатный процесс- это процесс без теплообмена с внешней средой. При адиабатном процессе энергообмен рабочего тела с окружающей средой происходит только в форме работы, энергообмена в форме теплоты нет. Эти условия выражаются соотношением:  . Тогда уравнение первого закона термодинамики для адиабатного процесса имеет вид:
. Тогда уравнение первого закона термодинамики для адиабатного процесса имеет вид:
 . (3.4)
. (3.4)
Из этого уравнения видно, что работа адиабатного процесса расширения совершается вследствие уменьшения внутренней энергии газа и, следовательно, температура газа уменьшается. Работа адиабатного сжатия полностью идет на увеличение внутренней энергии газа, то есть на повышение его температуры. Таким образом, изменение внутренней энергии и работа в адиабатном процессе эквивалентны по величине и противоположны по знаку.
Выведем уравнение адиабаты для идеального газа. Воспользуемся уравнением первого закона термодинамики:

т.к.  , то
, то
 (3.5)
(3.5)
Разделив переменные, получим:
 (3.6)
(3.6)
Интегрируя (5.6) при k = const, получим  , откуда
, откуда
 (3.7)
(3.7)
Уравнение (3.7) является уравнением адиабаты.
На рис. 3.7 приведен адиабатный процесс расширения газа в  -диаграмме.
-диаграмме.
Из уравнения (3.7) следует:
 , (3.8)
, (3.8)
то есть при адиабатном расширении давление падает, а при сжатии возрастает.

Рисунок 3.7 - Адиабата идеального газа
Учитывая, что в адиабатном процессе изменяются все три параметра состояния, необходимо выявить зависимости между v и T, p и T.
Зависимость между температурой T и объемом v можно получить из уравнения (5.8) и уравнений состояния, записанных для точек процесса 1 и 2: Р1v1 = RT1 и Р2v2=RT2, откуда
 (3.9)
(3.9)
Из уравнений (3.8) и (3.9) следует: 
 (3.10)
(3.10)
Далее из уравнений (3.8) и (3.10) следует: 
 (3.11)
(3.11)
При k = const для вычисления работы адиабатного процесса можно записать несколько формул. Из уравнения  при cv = const имеем:
при cv = const имеем:
 (3.12)
(3.12)
Учитывая соотношения (3.10) и (3.11), уравнение (3.12) запишем в виде:

(3.13)

Располагаемая работа в адиабатном процессе определим из соотношения
 , то есть
, то есть
 (3.14)
(3.14)
Для обратимого адиабатного процесса  , поэтому
, поэтому
 , то есть обратимый адиабатный процесс будет изоэнтропным и в
, то есть обратимый адиабатный процесс будет изоэнтропным и в 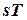 -диаграмме изображается прямой линией, параллельной оси
-диаграмме изображается прямой линией, параллельной оси  (рис. 3.8). Процесс адиабатного расширения изображается вертикальной прямой 2-1, идущей вниз, а процесс адиабатного сжатия 1-2 – вертикальной прямой, идущей вверх.
(рис. 3.8). Процесс адиабатного расширения изображается вертикальной прямой 2-1, идущей вниз, а процесс адиабатного сжатия 1-2 – вертикальной прямой, идущей вверх.

Рисунок 3.8 - Адиабатный процесс в 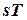 -диаграмме
-диаграмме
Теплоемкость в адиабатном процессе равна нулю:  .
.
Политропный процесс
Политропный процесс – любой произвольный процесс изменения состояния рабочего тела, протекающий при постоянной теплоемкости сx, то есть c = cx = const. Линия процесса называется политропой.
Из определения политропного процесса следует, что основные термодинамические процессы (изохорный, изобарный, изотермический, адиабатный, если они протекают при постоянной удельной теплоемкости, являются частными случаями политропного процесса.
Другими словами, политропный процесс характеризуется одной и той же долей количества подводимой теплоты, расходуемой на изменение внутренней энергии системы.
Уравнение политропного процесса можно получить из уравнений первого закона термодинамики для идеального газа:


далее имеем:

Разделим первое уравнение на второе

и обозначим
 ,
,
тогда

Интегрируя полученное соотношение в пределах от начала до конца процесса, находим:
 , (3.15)
, (3.15)
или после потенцирования
 (3.16)
(3.16)
получаем уравнение политропного процесса 
Поскольку уравнение политропы отличается от уравнения адиабаты только значением показателя n, то все соотношения между основными параметрами могут быть представлены формулами, аналогичными формулам для адиабатного процесса:
 . (3.17)
. (3.17)
Удельная теплоемкость политропного процесса может быть определена из выражения для показателя политропы
 , откуда
, откуда  ,
,
где k – показатель адиабаты.
Последнее уравнение позволяет определить удельную теплоемкость политропного процесса для любого значения n. Если в это уравнение подставить значения для частных случаев, то можно получить:
| Изохорный процесс: | n = ±¥; | c = cv; | v = const. | |
| Изобарный процесс: | n = 0; | c = kcv = cp; | p = const. | |
| Изотермический процесс: | n = 1; | c = ±¥; | T = const. | |
| Адиабатный процесс: | n = k; | c = 0; | pvk = const. | |
Характер зависимости 
 от показателя политропы n графически показан на рисунке 3.9.
от показателя политропы n графически показан на рисунке 3.9.

Рисунок 3.9 - Зависимость теплоемкости от показателя политропы
Уравнение удельной работы изменения объема, совершаемой телом при политропном процессе, имеет аналогичный вид с уравнением удельной работы в адиабатном процессе
 (3.18)
(3.18)
или
 . (3.19)
. (3.19)
Располагаемая работа равна: 
 . (3.20)
. (3.20)
Изменение удельной внутренней энергии газа и теплота в политропном процессе определяются из уравнений:
 (3.21)
(3.21)
 . (3.22)
. (3.22)
Изменение удельной энтальпии определяется по формуле, справедливой для всех процессов идеального газа, включая политропный процесс:
 . (3.23)
. (3.23)
Изменение удельной энтропии газа в политропном процессе равно:
 , (3.24)
, (3.24)
или для конечного изменения состояния
 . (3.25)
. (3.25)
Значение показателя политропы в любом политропном процессе может быть определено по координатам любых двух точек графика:
 ;
;  ;
;  . (3.26)
. (3.26)
Если в vP- и sT – координатах выбрать некоторую произвольную точку и провести из нее все рассмотренные термодинамические процессы, то все поле построенной таким образом диаграммы делится на восемь областей, характеризующихся определенными признаками (рис. 3.10).

Рисунок 3.10 - Взаимное расположение политроп в зависимости от величины показателя n
Литература: [2], с. 24-37; [5], с. 12-20; [6], с. 21-31; [8], с. 259-285.
Вопросы для самоконтроля
1. Изобразите наvP- иsT-диаграммах изобарный и изохорный процессы для идеального газа.
2. Изобразите на vPи sT-диаграммах изоэнтальпийный и энтропийный процессы для идеального газа.
3. Какие процессы в термодинамике называются основными?
4. Как называется процесс, в котором все подведенное тепло идет на увеличение внутренней энергии?
5. Чему равен показатель адиабаты в изотермическом процессе идеального газа?
6. Как называется процесс, в котором работа совершается только за счет изменения внутренней энергии?
7. Как называется процесс, в котором энтальпия остается неизменной?
8. Изобразите на sT-диаграмме процесс сжатия Pvnи покажите, какими площадками будет изображаться q, Du.
4 второй закон термодинамики
