Расчет двухстадиальных схем с замкнутыми циклами измельчения
Схемы приведены на рис. 4.15. Первая стадия в этих схемах представлена разновидностью В, вторая стадия может быть представлена одной из следующих разновидностей А, А', В, Е.
При расчете двухстадиальных схем с замкнутыми циклами могут быть поставлены две задачи: первая - при известных Q1,b1 , bк , Rc , Rп, m, и k требуется определить массы и выходы всех продуктов; вторая – при известных Q1, b1 , bк , b4, Rc , Rп, m, k требуется определить соотношение объемов m мельниц второй и первой стадий измельчения, массы и выходы всех продуктов.
Если задано m, то этим уже определяется крупность слива классификации первой стадии измельчения. Наоборот, если задана крупность слива классификации первой стадии, то этим обуславливается соотношение объемов мельниц m.
В установившемся режиме Q1 = Q4 = Qк; Q2 = Q3 .
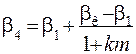 . (4.72)
. (4.72)
Далее схемы первой и второй стадий рассчитываются как одностадиальные схемы с заданными значениями Сопт.
Соотношение объемов мельниц первой и второй стадий
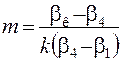 . (4.73)
. (4.73)
Расчет двухстадиальных схем с частично замкнутым циклом измельчения
Схемы ЖВ и ЖД приведены на рис. 4.16. Расчет рассмотрим на примере схемы ЖВ. Исходные данные для расчета: Q1,b1, b4, b10, m, k, R4 и R5. Требуется определить: массы и выходы всех продуктов в схеме; отношение n, в котором необходимо делить пески в точке А, 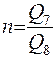 .
.
В установившемся режиме Q1 = Q12; Q2 = Q3; Q6 = Q10 и Q8 = Q9. Так как в сливах обоих классификаторов получается окончательный продукт, то b4 » b10 » b12.
Для определения массовой доли расчетного класса в питании классификаторов первой стадии b3 сначала находим b'3 - массовую долю в продукте 3 класса крупности минус 0,04 мм.
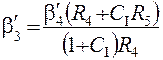 , (4.74)
, (4.74)
где СI – циркулирующая нагрузка первой стадии измельчения,
определяемая отношением Q5: Q4.
Значение b'4 находим из табл. 4.10 по заданному b4. Зная b'3 по табл. 4.10 находим значение b3.
Масса продукта 6 определяется по уравнению 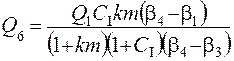 . (4.75)
. (4.75)
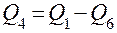 .
.
Если в измельчение поступает руда с небольшой массовой долей расчетного класса (b1 < 5 %), то приближенно можно считать, что производительность стадии измельчения по выдаваемому готовому продукту пропорциональна приведенном объему мельниц и их удельной производительности по вновь образованному расчетному классу. Тогда
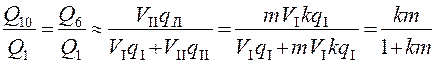 ; (4.76)
; (4.76)
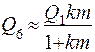 . (4.77)
. (4.77)
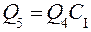 ;
; 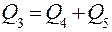 ;
; 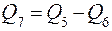 ;
; 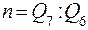 .
.
Вторая стадия измельчения является схемой В с исходным питанием Q6.
Примеры расчета схем измельчения
Пример 1. Рассчитать схему Д (рис. 4.12) Исходные данные для расчета: Q1= 200 т/ч; b4 = 50 %, b6 = 75 %, R6 = 2,6 (28 % твердого); R7 =0,4 (классификация в гидроциклонах).
По табл. 4.10 находим b'4 = 31,5 % и b'6 = 53 %.
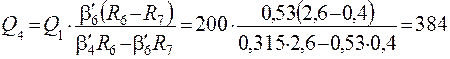 т/ч.
т/ч.
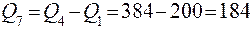 т/ч.
т/ч.
Назначаем оптимальную циркулирующую нагрузку Сопт= 300 %.
Тогда
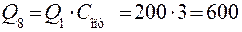 т/ч;
т/ч;
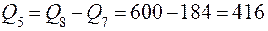 т/ч;
т/ч;
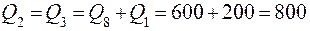 т/ч.
т/ч.
Пример 2. Определить при исходных данных примера 1 крупность продукта 4, если Q4= 250 т/ч.
|
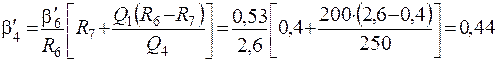
По табл. 4.10 находим b4 = 65 %.
Пример 3. Рассчитать схему ЖВ (рис. 4.16). Исходные данные для расчета: Q1= 200 т/ч; b1 = 5 %. b4 = b10 = b12 = 65 %, m = 1; k = 0,82; R4 = 0,82; R5=0,2 (классификация в спиральных классификаторах).
По табл. 4.10 находим по заданному b4 значение b'4. Задаемся оптимальным значением циркулирующей нагрузки Сопт = 150 %.
Тогда
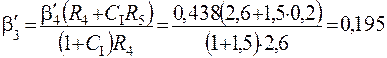 (19,5 %).
(19,5 %).
По табл. 4.10 находим b3 = 33,2 %.
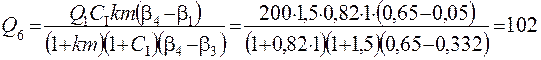 т/ч.
т/ч.
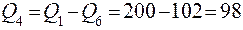 т/ч;
т/ч;
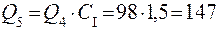 т/ч;
т/ч;
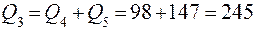 т/ч;
т/ч;
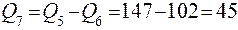 т/ч;
т/ч;
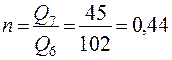 (44 %).
(44 %).
Выбираем оптимальную циркулирующую нагрузку для второй стадии измельчения СII = 300 %.
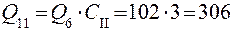 т/ч;
т/ч;
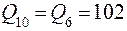 т/ч;
т/ч;
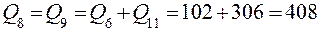 т/ч.
т/ч.
Пример 4. При исходных данных примера 3 определить массу продукта 6, если СI = 250 %.
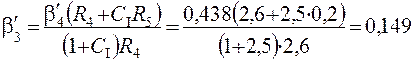 (14,9) %.
(14,9) %.
По табл. 4.10 находим b3 =25,8 %.
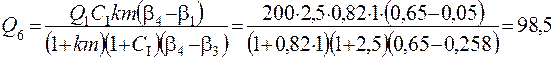 т/ч.
т/ч.
