Движение заряженных частиц в магнитном поле

Сила Лоренца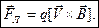

Т.к. 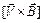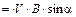, то;

Модуль силы Лоренца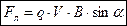

где q - величина заряда;

V - скорость заряженной частицы;

B - индукция магнитного поля;

α - угол между направлением векторов скорости и индукции

Направление действия этой силы, может быть определено для положительных зарядов с помощью «правила левой руки»: если расположить левую руку так, чтобы силовые линии поля входили в ладонь, а четыре пальца указывали направление вектора скорости, то большой палец укажет направление действия силы. Для отрицательных зарядов направление действия силы противоположное.

По международным стандартам именно через силу Лоренца определяется единица индукции - тесла, равная магнитной индукции однородного магнитного поля, в котором на заряженную частицу с зарядом 1 Кл, движущуюся перпендикулярно линиям индукции со скоростью 1 м/с, действует сила 1 Н.

Полная сила Лоренца, действующая на носитель заряда в электромагнитном поле равна

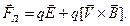
Движение заряженных частиц в магнитном поле

1. При V = 0 F_л = 0 (на неподвижный заряд магнитное поле не действует).

2. При α = 0^о (заряд влетает в параллельное поле ) sin α = 0 → F_л = 0.

3.При α = 90^о → sin α = 1 →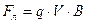

Если частица массой m с зарядом q влетает в однородное магнитное поле с индукцией 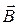перпендикулярно его силовым линиям, то под действием силы Лоренца она приобретает нормальное ускорение, перпендикулярное плоскости векторов скорости и индукции:

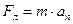
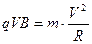
Модуль скорости частицы при этом меняться не будет, поскольку сила, перпендикулярная перемещению, работы не совершает.

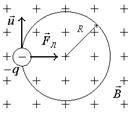Траекторией движения такой частицы будет окружность радиуса R:

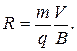
Период обращения частицы не зависит от скорости движения

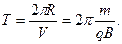
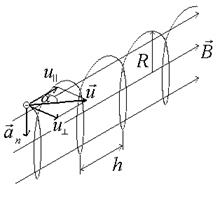
4.При 0⁰ < α < 90⁰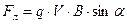

Если частица влетает в магнитное поле под углом a к силовым линиям, то составляющая скорости, перпендикулярная силовым линиям (V_^ = V∙sin α ), обеспечит движение по окружности радиуса R , а параллельная составляющая (V_׀׀ = V∙cos α ) – поступательное движение. В результате траектория частицы будет представлять собой винтовую линию с шагом h. Радиус винтовой линии рассчитаем на основании закона Ньютона

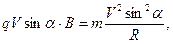
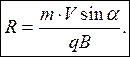
Шаг винтовой линии h равен пути, который проходит частица с параллельной составляющей скорости за время одного периода T:

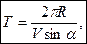
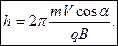
Работа силы Лоренца равна нулю независимо от массы частицы, заряда и траектории движения, так как Fл всегда перпендикулярна направлению скорости

Применение силы Лоренца

1. Масс-спектрометры

На применении силы Лоренца основана работа масс-спектрометров, с помощью которых определяют массы заряженных частиц.

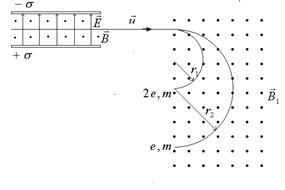Пучок заряженных частиц, ускоренный разностью потенциалов, влетает в селектор, представляющий собой заряженный конденсатор, находящийся в магнитном поле, перпендикулярном силовым линиям электрического поля. Сквозь селектор могут прорваться только частицы, для которых сила Лоренца уравновешивает силу Кулона (остальные частицы отклоняются и оседают на пластины)

→

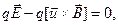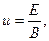
.Отобранные частицы равных скоростей попадают в магнитное поле индукцией 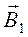, перпендикулярное направлению скорости частиц, и движутся по круговой траектории с радиусом

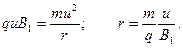
Удельный заряд частицы на фотографии её трека в магнитном поле определяется радиусом траектории

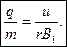
Если известен заряд частицы, рассчитывают её массу. Так, систематически измеряя массы атомных ядер, обнаружили существование изотопов.

2. Ускорители заряженных частиц:

a) Линейный ускоритель (ускорение частиц до энергии ≈ 10 МэВ);

b) Циклотрон (ускорение протонов до энергии ≈ 20 МэВ);

c) Фазотрон (ускорение протонов до энергии ≈ 1 ГэВ);

d) Синхротрон (ускорение электронов до энергии ≈ 10 ГэВ);

e) Синхрофазотрон (ускорение тяжелых заряженных частиц , например, протонов и ионов до энергии ≈ 500 ГэВ)