Закон Био – Савара – Лапласа

И его применение к расчету магнитных полей

Для проводника с током I , элемент которого dl создает в некоторой точке А индукцию поля dB:

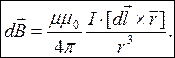(1)

где 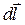вектор, равный длине dl , совпадает по направлению с током I

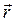радиус–вектор , проведенный из dl в точку А

r модуль вектора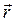

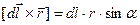- модуль векторного произведения (2)

α - угол между 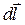и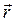

Если подставить (2) в (1), получим формулу для расчета модуля вектора магнитной индукции ;

Модуль вектора индукции 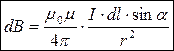(3)

Принцип суперпозиции магнитных полей

Примеры расчёта магнитных полей

a) Поле прямолинейного проводника с током

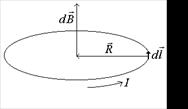
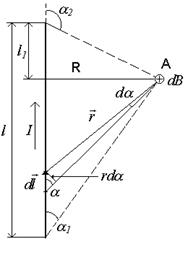Рассмотрим отрезок проводника длиной l с током I. Пусть интересующая нас точка А поля находится на расстоянии R от проводника. Произвольно выберем на проводнике

бесконечно малый элемент 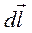с током и проведём от него радиус-вектор 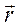в интересующую нас точку. Элементарные индукции магнитного поля 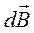, созданные такими элементами направлены вдоль одной прямой перпендикулярно плоскости рисунка от нас.

Результирующая индукция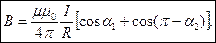

Если проводник имеет бесконечную длину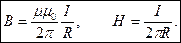

b) Поле в центре кругового тока.

На рис. представлен круговой виток радиуса R, обтекаемый током I. Элементарные значения индукции, создаваемые элементами токов в центре кольца сонаправлены и параллельны плоскости витка.

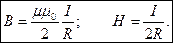
c) Поле на оси витка.

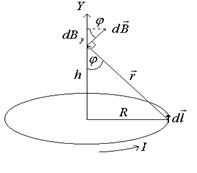
Индукция поля на оси (на рисунке Y) витка, , направлена вдоль этой оси.

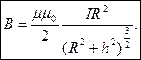
d) Поле в центре соленоида.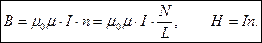

N – число витков соленоида;

L - длина соленоида;

n = N/L - число витков на единицу длины соленоида.

Вектор индукции магнитного поля параллелен оси соленоида

e) Поле тороида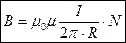

N – число витков соленоида;

R – радиус тороида.

Закон Ампера. Взаимодействие параллельных токов.

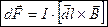
Сила, dF, с которой магнитное поле действует на элемент проводника dl c током, находящегося в магнитном поле, прямо пропорциональна силе тока I, и векторному произведению элемента длины dl проводника на магнитную индукцию В:

Направление силы Ампера определяется правилом левой руки:

Если левую руку расположить так, чтобы вектор В входил в ладонь, а четыре вытянутых пальца указывали направление тока в проводнике, то большой отогнутый палец покажет направление силы, действующей на проводник с током.

Модуль силы Ампера;

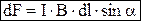
При dl _┴ B, sinα = 1, тогда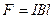

Отсюда физический смысл индукции В:

Это сила, с которой магнитное поле действует на проводник длиной 1м, по которому течет ток 1А

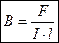
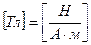
Закон Ампера применяется для определения силы взаимодействия двух токов.

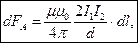
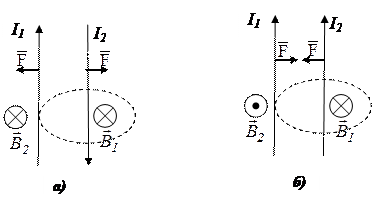
Это взаимодействие проявляется в притяжении и отталкивании, однако, не является кулоновским. Отталкиваются (рис. а) проводники с токами противоположно направленными, притягиваются одинаково направленные токи (рис. б).

Сила Лоренца.