Стационарная теплопроводность в телах классичес-кой формы (пластина, цилиндр, шар). Определение количест-ва передаваемой теплоты.

Плоская стенка

При установившемся или стационарном тепловом режиме температура тела во времени остается постоянной, т.е. 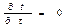. Если внутренние источники теплоты отсутствуют ( 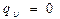), то уравнение Фурье имеет вид:

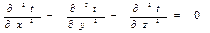
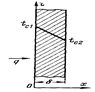Рассмотрим изотропную стенку толщиной δ, высота и ширина которой являются величинами бесконечно большими относительно толщины δ, с посто­янным коэффициентом теплопроводности λ. На наружных поверхностях стенки поддерживаются постоянными температуры t_с1 и t_с2.

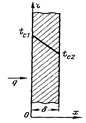При заданных условиях температура будет изме­няться только в направлении, перпендикулярном пло­скости стенки. Если ось Ох направить, как показано на рисунке, то температура в направлении осей Оуи Oz будет оставаться постоянной

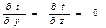
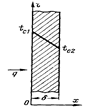Температура будет функцией только одной координаты х и уравнение теплопроводности для рассматриваемого случая запишется

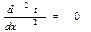
Зададим граничные условия в рассматриваемой задаче:

при х = 0 t = t_с1

при х = δ t = t_с2

В результате решения поставленной задачи должно быть найдено распределение температуры в плоской стенке, т.е. t = f(x), и получена формула для определения количества теплоты, проходящего в единицу времени через стенку.

Закон распределения температур по толщине стенки найдется в ре­зультате двойного интегрирования уравнения Фурье.

Первое интегрирование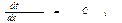

Второе интегрирование

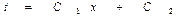
Постоянные С₁ и С₂ определяются из граничных условий:

при х = 0 и t = t_с1 С₂ = t_c1

при х = δ и t = t_с2

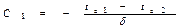
В итоге, закон распределения температуры в рассматриваемой плоской стенке

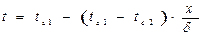
Для определения количества теплоты, про­ходящего через единицу поверхности стенки в единицу времени в направлении оси Ох, вос­пользуемся законом Фурье

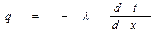, а

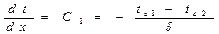
Следовательно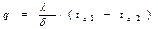

Из уравнения следует, что количество теплоты, проходящее через единицу поверхности стенки в единицу времени, прямо пропорцио­нально коэффициенту теплопроводности λ, разности температур на на­ружных поверхностях стенки (t_с1 – t_с2) и обратно пропорционально тол­щине стенки δ.

Отношение δ/λ, (м²·К)/Вт называется тепловым или термическим со­противлением стенки.

Зная плотность теплового потока, легко вычислить общее количество теплоты 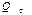, Дж, которое передаётся через поверхность стенки величиной F за промежуток времени τ.

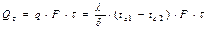
Рассмотрим теплопроводность многослойной плоской стенки, состо­ящей из n однородных слоев. Примем, что контакт между слоями со­вершенный и температура на соприкасающихся поверхностях двух сло­ев одинакова.

При стационарном режиме тепловой поток, проходящий через лю­бую изотермическую поверхность неоднородной стенки, один и тот же.

При заданных температурах на внешних поверхностях такой стенки, размерах слоев и соответствующих коэффициентах теплопроводно­сти можно составить систему уравнений

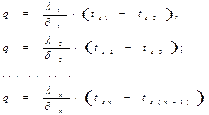
Выразив температурные напоры в каждом слое и сложив правые и левые части полученных уравнений, будем иметь:

.

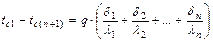Отсюда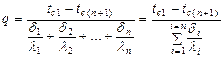

Величина 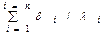, равна сумме термических сопротивлений всех n слоев, называется полным термическим сопротивлением теплопроводности многослойной стенки.

Цилиндрическая стенка

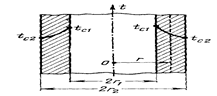
Рассмотрим стационарный процесс теплопроводности в цилиндри­ческой стенке (трубе) с внутренним диаметром d₁=2r₁ и наружным ди­аметром d₂=2r₂.

На поверхностях стенки заданы постоянные температуры t_с1 и t_с2. В заданном интервале температур коэффициент теплопроводности ма­териала стенки λ является постоянной величиной.

Необходимо найти распределение температур в цилиндрической стенке и тепловой поток через нее.

В рассматриваемом случае дифференциальное уравнение теплопро­водности удобно записать в цилиндрической системе координат

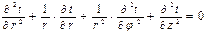
При этом ось Oz совмещена с осью трубы.

При заданных условиях температура изменяется только в радиаль­ном направлении и температурное поле будет одномерным. Поэтому

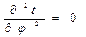и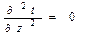

Уравнение Фурье примет вид:

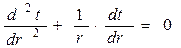
Граничные условия:

при r = r₁ t = t_c1

при r = r₂ t = t_c2

Введём новую переменную 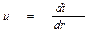, тогда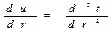

Подставляя в уравнение Фурье, получим:

,

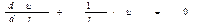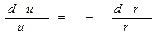
Интегрируя, получаем:

^{-> -> ->} .

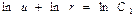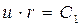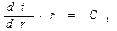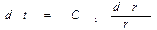После интегрирования

(*)

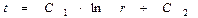Подставляя граничные условия

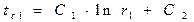
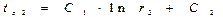Решение уравнений дает:

.

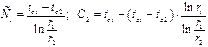Подставив значения С₁ и С₂ в уравнение (*), получим:

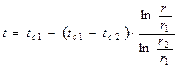или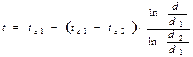

Для нахождения количества теплоты, Вт, прохо­дящего через цилиндрическую поверхность вели­чиной F в единицу времени, можно воспользо­ваться законом Фурье

.

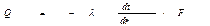Учитывая, что F=2π·r·l и 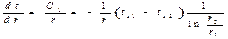получаем 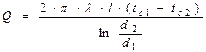, Вт.

Следовательно, количество теплоты, проходящее через цилиндрическую стенку в единицу времени, определя­ется заданными граничными условиями и не зависит от радиуса.

Тепловой поток Q может быть отнесен либо к единице длины трубы, либо к единице внутренней или внешней поверхности. При этом расчетные формулы для плотности теплового потока, Вт/м², прини­мают вид

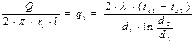
(тепловой поток через единицу внутренней поверхности);

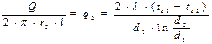
(тепловой поток через единицу наружной поверхности);

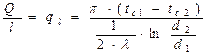
(тепловой поток, проходящий через единицу длины трубы, Вт/м).

Основные понятия конвективного теплообмена.

Понятие конвективного теплообмена охватывает процесс теплообмена при движении жидкости или газа. При этом перенос теплоты осуществляется одновременно конвекцией и теплопроводностью.

Если в единицу времени через единицу контрольной поверхности нормально к ней проходит масса жидкости , кг/(м²·с), где – скорость, – плотность жидкости, то вместе с ней переносится теплота, Вт/м²:

Конвекция теплоты всегда сопровождается теплопроводностью, т.к. при движении жидкости или газа происходит сопри­косновение отдельных частиц, имеющих различные температуры. В результате конвективный теплообмен описывают уравнением

При расчетах конвективного теплообмена между текущей жидкостью и твёрдой стенкой используют закон Ньютона – Рихмана:

Коэффициент теплоотдачи α зависит от большого количества факто­ров. В общем случае α является функцией

- формы и размеров тела,

- ре­жима движения,

- скорости и температуры жидкости,

- физических па­раметров жидкости,

- других величин.

Чтобы привести жидкость в движение, к ней необходимо при­ложить силу. Силы, действующие на какой-либо элемент жидкости, можно разделить на массовые (или объемные) и поверхностные.

Массовыми называют силы, приложенные ко всем частицам жид­кости и обусловленные внешними силовыми полями (например, грави­тационным или электрическим).

Поверхностные силы возникают вслед­ствие действия окружающей жидкости или твердых тел; они приложены к поверхности контрольного объема жидкости. Такими силами являют­ся силы внешнего давления и силы трения.

Различают свободную и вынужденную конвекцию.

В пер­вом случае жидкость с неодно­родным распределением температуры, и, как следствие, с неоднород­ным распределением плотности, находится в поле земного тяготения. Поэтому в ней может возникнуть свободное гравитационное движение.

Вынужденное движение объема жидкости про­исходит под действием внешних поверхностных сил, приложенных на его границах, за счет предварительно сообщенной кинетической энер­гии (например, за счет работы насоса, вентилятора, ветра).

Вынужденное движение в общем случае может сопровождаться свободным движением. Относительное влияние последнего тем больше, чем больше разница температур отдельных частиц среды и чем меньше скорость вынужденного движения.