Электромагнитная индукция. Явление взаимной индукции. Взаимная индуктивность. Энергия системы проводников с током. Плотность энергии магнитного поля.

Явление электромагнитной индукции : при изменении магнитного поля внутри замкнутого контура в нём возникает электрический ток, который называют индукционным током(см вопрос 21)

Взаимная индукция-явление возникновения ЭДС в одном из контуров при изменении силы тока в другом.

Возьмем 2 СВЯЗНЫХ контура:

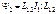-к-т взаимоиндукции-взаимная индуктивность

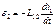
Плотность энергии:

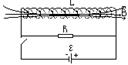Рассмотрим цепь:

При замкнутом ключе- в соляноиде-ток I.

Размыкаем-через сопротивление некоторое время течет убывающий ток I , поддерживаемый ЭДС самоиндукции соляноида. Работа этого тока за dt равна :

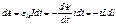
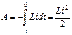-идет на приращение внутренней энергии системы.: W=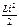

Выразим энергию через Н и В: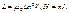

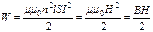
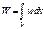
Полученная формула показывает, что энергия поля рассредоточена по всему объему, занимаемому полем, с плотностью энергии.

Для энергии связанных друг с другом N контуров :

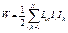
24. Дифференциальное уравнение затухающих колебаний (механических и электрических) и его решений.

Логарифмический декремент и коэффициент затухания.

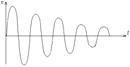
Затухающие колебания -колебания, энергия которых уменьшается с течением времени за счет действия сил сопротивления.

1. Механические:

Пусть F_сопр=-hv(сила сопротивления пропорциональна скорости колебаний)= - hx¢, h-к-т сопротивления.

Тогда по 2-му з-ну Ньютона:mx¢¢=- hx¢ - кх(=Fтр).

Обозначим:b=h/2m-коэффициент затухания ; w₀²=k/m-собственная частота свободных колебаний.

x¢¢+2bх¢+w₀²х=0

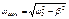-собственная частота свободных незатухающих колебаний(-сколько раз за p секунд тело пройдет через положение равновесия)

При условии b>w₀-затух колебаний нет - апериодический возврат в положение равновесия

При условии b<w₀-затухающие колебания

Решение уравнения - х(t)=а₀е^-btcos(wt+a) a-начальная фаза.

Логарифмический декремент и коэффициент затухания:

Если A(t), A(t+T), амплитуды двух последовательных колебаний то отношение 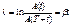называется логарифмическим декрементом затухания

Электрические

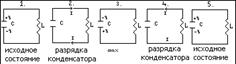рис: свободные э-м колебания-идеальный случай

2.разряд кондера. Благодаря самоиндукции(заключается в появлении ЭДС индукции в самом проводнике при изменении тока в нем.)- ток растет до амплитудного значения. 3.ток , сохраняя направление уменьшается до 0. заряд кондера и разность потенциалов между обкладками-max, но знаки –поменялись. 4.-5. обратный процесс.

колебательный контур=индуктивность+конденсатор+резистор(но его может и не быть , тк каждый контур обладает активным сопротивлением R.) Энергия контура постоянно расходуется на выделение тепла.

Уравнение свободных колебаний:q¢¢+w₀²q=0: Т=2p 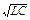-период Q(t)=q_mcos(w₀t+j); Uc= q_mcos(w₀t+j)/C;Um=Im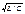

I(t)=I_mcos(w₀t+j+p/2)

Уравнение вынужденных колебаний: q¢¢+bq¢+w₀²q=0

При условии b>w₀-затух колебаний нет - апериодические

При условии b<w₀-затухающие колебания

Решение уравнения - q(t)=q_mе^-btcos(wt+j)

Лог декремент: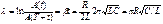

Q=p/l-ДОБРОТНОСТЬ характеризует колебательную систему, при малых значениях логарифмического декремента

25. Дифференциальное уравнение вынужденных колебаний и его решение. Амплитуда и фаза вынужденных колебаний. Резонанс.Резонансные кривые колебательного контура. Добротность.

Колебания возникающие под действием внешней периодически изменяющейся силы называются вынужденными колебаниями.

1. Механические:

Обозначим:b=h/2m-коэффициент затухания ; w₀²=k/m-собственная частота свободных колебаний.f₀=F₀/m

x¢¢+2bх¢+w₀²х=f₀coswt-неоднородное линейное уравнение 2-го порядка

Решение: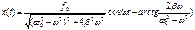

Электрические

q¢¢+2bq¢+w₀²q=f_mcoswt, f_m=U_m/l

w _рез=w₀²-2b²

U_c=q_m/C

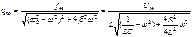
Добротность конденсатора показывает –во сколько раз напряжение на конденсаторе может превысить приложенное.

I(t)=-wq_msin(wt-j)=ImCOS(wt-j+p/2)

Im=q_mw=Um/R

Q=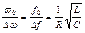

26. Система уравнений Максвелла в интегральной форме. Материальные уравнения.

1. Закон эл-магн индукции: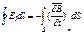

2. Линии B- замкнуты :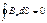

3. Связь между токами проводимости и смещения и создаваемыми ими уравнениями: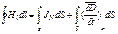

4. Теорема Гаусса: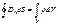

+материальные уравнения:

1. `D=ee<sub>0</sub>`E-см далее

2. `B=mm<sub>0</sub>`H

3. `J=d`E-в-р плотности тока пропорционален напряженности поля

где введены следующие обозначения:

`E- напряженность электрического поля (В / м).

`H- напряженность магнитного поля (А / м).

`D - электрическая индукция (Кл / м2).

`B - магнитная индукция (Т).

r- плотность заряда (Кл / м3).

j- плотность тока (А / м2).

q- электрический заряд (Кл).

I- электрический ток (А).

При рассмотрении полей в различных средах вводятся соотношения между напряжениями и индуктивностями, а также между электрическим током и напряженностью электрического поля Приближенно для линейной, изотропной безинерционной среды можно записать:D=ee₀`E

s- удельная проводимость

27. Система уравнений Максвелла в дифференциальной форме. Волновое уравнение (вывод) для электромагнитных волн.

материальные уравнения:

1. `D=ee<sub>0</sub>`E-вектор электрической индукции пропорционаленнапряженности поля

2. `B=mm<sub>0</sub>`H

3. `J=d`E-в-р плотности тока пропорционален напряженности поля

`В- вектор магнитной индукции [Тл=F_m/IÙl],

`H- вектор напряженности магнитного поля [А/м]

+Максвелл в дифференциальной форме

1. [Ñ E]=-d B / d t-з-н э-м индукции

2. Ñ B=0-отсустствие магнитных зарядов

3. [Ñ E]=j+ d D / d t-связь токов проводимости и смещения

4. Ñ D=r -источник D -есть сторонние заряды