Испарение и кипение. Плавление и кристаллизация.

Испарение, кипение.

Испарение- парообразование, происходящее с поверхности жидкости. Скорость испарения зависит от рода жидкости. Испарение происходит при любой температуре и возрастает с ее повышением. Испарение происходит с поверхности жидкости и увеличивается при увеличении этой поверхности. При ветре испарение происходит быстрее. Испарение увеличивается при уменьшении давления. Твердые тела тоже могут испаряться. Внутренняя энергия испаряющейся жидкости уменьшается. Если нет притока энергии извне, то испаряющаяся жидкость охлаждается. Кипение- это интенсивный переход жидкости в пар вследствие образования и роста пузырьков пара, которые при определенной температуре для каждой жидкости всплывают на ее поверхность и лопаются. Температура кипения- это температура, при которой жидкость кипит. Во время кипения температура жидкости не меняется.

Плавле́ние —это процесс перехода тела^{[источник не указан 1002 дня]} из кристаллического твёрдого состояния в жидкое. Плавление происходит с поглощением удельной теплоты плавления и является фазовым переходом первого рода.

Способность плавиться относится к физическим свойствам вещества ^[1]При нормальном давлении, наибольшей температурой плавления среди металлов обладает вольфрам (3422 °C), среди простых веществ - углерод (по разным данным 3500 — 4500 °C^[2]) а среди произвольных веществ — карбид тантала-гафния Ta₄HfC₅ (4216 °C). Можно считать, что самой низкой температурой плавления обладает гелий: при нормальном давлении он остаётся жидким при сколь угодно низких температурах.

Многие вещества при нормальном давлении не имеют жидкой фазы. При нагревании они путем сублимации сразу переходят в газообразное состояние

Б 38

Граничные условия Еn и Еt.

В проводящем теле, находящемся в электростатическом поле, все точки тела имеют одинаковый потенциал, поверхность проводящего тела является эквипотенциальной поверхностью и линии напряженности поля в диэлектрике нормальны к ней. Обозначив через Е_n и Е_t нормальную и касательную к поверхности проводника, составляющие вектора напряженности поля в диэлектрике около поверхности проводника, указанные условия можно записать в виде:

Е_t = 0; Е = Е_n = -¶U/¶n; D = -e*¶U/¶n = s,

где s – поверхностная плотность электрического заряда на поверхности проводника.

Таким образом, на границе раздела проводящего тела и диэлектрика отсутствует касательная к поверхности (тангенциальная) составляющая напряженности электрического поля, а вектор электрического смещения в любой точке, непосредственно примыкающей к поверхности проводящего тела численно равен плотности электрического заряда s на поверхности проводника

Б 29

Теорема Клаузиуса, неравенство Клаузиуса. Энтропия, её физический смысл. Изменение энтропии при необратимых процессов. Основное уравнение термодинамики.

сумма приведенных теплот при переходе из одного состояния в другое не зависит от формы (пути) перехода в случае обратимых процессов. Последнее утверждение носит название теоремы Клаузиуса.

Рассматривая процессы превращения тепла в работу, Р. Клаузиус сформулировал термодинамическое неравенство, носящее его имя.

«Приведенное количество тепла, полученное системой в ходе произвольного кругового процесса, не может быть больше нуля»

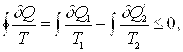
где dQ – количество тепла, полученного системой при температуре Т, dQ₁ - количество тепла, получаемое системой от участков окружающей среды с температурой Т₁, dQ^¢₂ – количество тепла, отдаваемое системой участкам окружающей среды при температуре Т₂. Неравенство Клаузиуса позволяет установить верхний предел термического К.П.Д. при переменных температурах нагревателя и холодильника.

Из выражения для обратимого цикла Карно следует, что или , т.е. для обратимого цикла неравенство Клаузиуса переходит в равенство. Это означает, что приведенное количество тепла, полученного системой в ходе обратимого процесса, не зависит от вида процесса, а определяется только начальным и конечным состояниями системы. Поэтому приведенное количество тепла, полученное системой в ходе обратимого процесса, служит мерой изменения функции состояния системы, называемой энтропией.

Энтропия системы – функция ее состояния, определенная с точностью до произвольной постоянной. Приращение энтропии равно приведенному количеству тепла, которое нужно сообщить системе, чтобы перевести ее из начального состояния в конечное по любому обратимому процессу.

, .

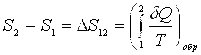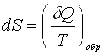Важной особенностью энтропии является ее возрастание в изолированных системах (закон возрастания энтропии).

«Энтропия теплоизолированной (адиабатической) системы не может убывать; она возрастает, если в системе идет необратимый процесс, и остается постоянной при обратимом процессе в системе».

Необратимые процессы в системе приводят к установлению равновесного состояния. В этом состоянии энтропия изолированной системы достигает максимума и в дальнейшем никакие макроскопические процессы в системе невозможны.

Изменение энтропии при наличии теплообмена с окружающей средой, может быть каким угодно, как больше нуля, так и меньше нуля.

Получим выражение для приращения энтропии идеального газа, при переходе из состояния с параметрами T₁, V₁, в состояние с параметрами T₂, V₂ .

.

Из выражения для приращения энтропии газа следует, что энтропия является функцией двух параметров - температуры и объема S=S(T,V).

Введение энтропии позволяет объединить первое и второе начала термодинамики в виде термодинамического неравенства

,

где знак = относится к обратимым процессам, знак > - к необратимым.

Энтропия, как и внутренняя энергия, связана с микроскопическим строением системы и статистическим характером теплового движения частиц системы. Это уравнение объединяет формулы первого и второго начала термодинамики:

dQ = dU + р dV, (3.42)

(3.43)
^ ВместоdQ в уравнение, выражающее второе начало термодинамики, подставим его выражение (3.42):

(3.44) Это и есть основное уравнение термодинамики.

Б 30

Свободная энергия. Энтальпия. Энтропия и вероятность. Статистический характер второго закона термодинамики. Тепловая смерть Вселенной.

Свобо́дная эне́ргия Гельмго́льца (или просто свобо́дная эне́ргия) — термодинамический потенциал, убыль которого в квазистатическом изотермическом процессе равна работе, совершённой системой над внешними телами.

Энтальпи́я, также тепловая функция и теплосодержание — термодинамический потенциал, характеризующий состояние системы в термодинамическом равновесии при выборе в качестве независимых переменных давления, энтропии и числа частиц.

Проще говоря, энтальпия — это та энергия, которая доступна для преобразования в теплоту при определенных температуре и давлении.

Определение энтропии и ее свойства. Величина, являющаяся функцией состояния, должна обладать свойством аддитивности. Действительно, макросистему всегда можно разбить на части и при этом функция состояния всей системы должна равняться сумме функций состояния ее частей.

Термодинамическая вероятность таким свойством не обладает. Покажем это на примере. Разобьем некую макросистему на две подсистемы, обладающие термодинамическими вероятностями W₁ и W₂. Число способов реализации данного состояния системы как единого целого для независимых событий равно произведению W = W₁·W₂.

Из курса математики известно, что логарифм произведения равен произведению логарифмов. Следовательно, логарифм термодинамической вероятности таким свойством обладает свойством аддитивности, т.е.

lnW = lnW₁ + lnW₂.

Величина, равная произведению постоянной Больцмана на логарифм термодинамической вероятности, называется энтропией S.
S = k·lnW. (15.3)

Свойства энтропии:

	энтропия является аддитивной величиной;
	энтропия - есть функция состояния макросистемы;
	энтропия изолированной системы при протекании необратимых процессов возрастает;
	энтропия макросистемы, находящейся в равновесном состоянии, максимальна.

Второе начало термодинамики. Второе начало термодинамики задает направленность процессов, протекающих в изолированной термодинамической системе. Оно гласит: изменение энтропии изолированной системы всегда положительно dS > 0 или равно нулю в случае достижения энтропией своего максимального значения.
Другими словами энтропия изолированной системы не может убывать.

Состояние с максимальным значением энтропии является равновесным. Еще раз отметим, что данная формулировка имеет статистический смысл, т.е. возможны некоторые отрицательные флуктуации изменения энтропии в отдельные моменты времени.

Тепловая смерть Вселенной» – гипотетическое состояние мира, к которому якобы должно привести его развитие в результате превращения всех видов энергии в тепловую и равномерного распределения последней в пространстве; в таком случае Вселенная должна прийти в состояние однородного изотермического равновесия, характеризуемого максимальной энтропией. Допущение тепловой смерти Вселенной формулируется на основе абсолютизации второго начала термодинамики, согласно которому энтропия замкнутой системы может только возрастать.

Б 35