Закон сохранения импульса в изолированной системе из двух материальных точек. Теорема о движении центра масс.

Рассмотрим систему, состоящую из n материальных точек. Между материальными точками действуют силы внутреннего взаимодействия 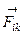, а также на материальные точки действуют внешние силы 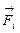. Здесь 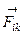- внутренняя сила, действующая на i-ю материальную точку со стороны k-й материальной точки, 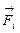- внешняя сила, действующая на i-ю материальную точку.

Система материальных точек называется замкнутой, если внешние силы отсутствуют, или их равнодействующая равна нулю: 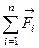= 0. Запишем для каждой материальной точки второй закон Ньютон.
Просуммировав левые и правые части этих уравнений, получим. Сумма производных равна производной от суммы, а также по третьему закону Ньютона: В результате получим: Если система материальных точек замкнута, т.е., тогда 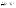= 0, и имеет место закон сохранения импульса:закон сохранения импульса системы материальных точек.
Если система материальных точек является замкнутой, то суммарный импульс системы остаётся постоянным, т.е. сохраняется во времени.
Если система не замкнута 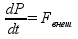. 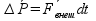– импульс силы, мера действия силы за некоторый промежуток времени.

Важное значение для системы материальных точек имеет такое понятие, как центр масс. Сначала рассмотрим две материальные точки с массами m₁ и m₂ и найдём их центр масс. В данном случае центр масс - это точка С, которая лежит на прямой соединяющей материальные точки. Если положение материальных точек описывается радиус-векторам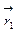и и 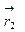, то положение центра масс С, будет описываться радиус-вектором 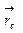, который равен

.

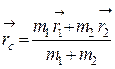. В общем случае системы из n материальных точек, положение центра масс будет описываться радиус-вектором: где M = m₁ + m₂ + ... + m_n - полная масса системы материальных точек. Взяв производную, получим скорость центра масс: Если система материальных точек замкнута, то, и тогда.

Таким образом, при отсутствии внешних сил центр масс системы материальных точек остается в покое или движется прямолинейно и равномерно

Центр масс системы движется так как двигалась бы м/т с массой равной масс всей системы под действием результирующей всех внешних сил действующих на систему

Б 7

Потенциальная энергия в поле центральных сил.

Центральным называют такое силовое поле, в котором потенциальная энергия частицы является функцией только от расстояния r до определенной точки- центра поля: U=U(r). Сила, действующая на частицу в таком поле, тоже зависит лишь от расстояния r и направлена в каждой точке пространства вдоль радиуса, проведенного в эту точку из центра поля.

Б 8

Понятие момента сил и момента импульса, связь между ними. Закон сохранения момента импульса. Момент силы (синонимы: крутящий момент; вращательный момент; вращающий момент) — физическая величина, характеризующая вращательное действие силы на твёрдое тело.

В физике момент силы можно понимать как «вращающая сила». В системе СИ единицами измерения для момента силы является ньютон-метр, хотя сантиньютон-метр (cN•m), футо-фунт (ft•lbf), дюйм-фунт (lbf•in) и дюйм-унция (ozf•in) также часто используются для выражения момента силы. Символ момента силы τ (тау). Момент силы иногда называют моментом пары сил, это понятие возникло в трудах Архимеда над рычагами. Вращающиеся аналоги силы, массы и ускорения есть момент силы, момент инерции и угловое ускорение соответственно. Сила, приложенная к рычагу, умноженная на расстояние до оси рычага, есть момент силы. Например, сила в 3 ньютона, приложенная к рычагу, расстояние до оси которого 2 метра, это то же самое, что 1 ньютон, приложенный к рычагу, расстояние до оси которого 6 метров. Более точно, момент силы частицы определяется как векторное произведение: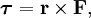

где 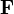— сила, действующая на частицу, и r — радиус-вектор частицы.

Момент импульса (кинетический момент, угловой момент, орбитальный момент, момент количества движения) характеризует количество вращательного движения. Величина, зависящая от того, сколько массы вращается, как она распределена относительно оси вращения и с какой скоростью происходит вращение.

Следует учесть, что вращение здесь понимается в широком смысле, не только как регулярное вращение вокруг оси. Например, даже при прямолинейном движении тела мимо произвольной воображаемой точки, оно также обладает моментом импульса. Наибольшую роль момент импульса играет при описании собственно вращательного движения.

Момент импульса замкнутой системы сохраняется.

Момент импульса 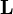частицы относительно некоторого начала отсчета определяется векторным произведением ее радиус-вектора и импульса: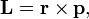

где 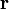— радиус-вектор частицы относительно выбранного начала отсчета, 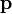— импульс частицы.

В системе СИ момент импульса измеряется в единицах джоуль-секунда; Дж·с.

Из определения момента импульса следует его аддитивность. Так, для системы частиц выполняется выражение:

.

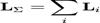В рамках закона сохранения момента импульса консервативной величиной является угловой момент вращения массы — он не изменяется в отсутствие приложенного момента силы или крутящего момента — проекции вектора силы на плоскость вращения, перпендикулярно радиусу вращения, помноженной на рычаг (расстояние до оси вращения). Самый расхожий пример закона сохранения момента импульса — фигуристка, выполняющая фигуру вращения с ускорением. Спортсменка входит во вращение достаточно медленно, широко раскинув руки и ноги, а затем, по мере того, как она собирает массу своего тела всё ближе к оси вращения, прижимая конечности всё ближе к туловищу, скорость вращения многократно возрастает вследствие уменьшения момента инерции при сохранении момента вращения. Тут мы и убеждаемся наглядно, что чем меньше момент инерции, тем выше угловая скорость и, как следствие, короче период вращения, обратно пропорциональный ей.

Закон сохранения момента импульса: Момент импульса системы тел сохраняется, если результирующий момент внешних сил, действующих на систему, равен нулю:

.

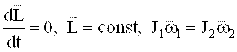Если результирующий момент внешних сил не равен нулю, но рана нулю проекция этого момента на некоторую ось, то проекция момента импульса системы на эту ось не изменяется.