Следовательно, ускорение системы
a = mg / (2M + m), м/с2 (1)
Так как все величины, стоящие в правой части выражения (1), остаются во время движения неизменными, то ускорение системы постоянно и движение системы равноускоренное. Кроме того, знаменатель дроби (2M + m) всегда значительно больше числителя mg, следовательно, ускорение a будет иметь значительно меньшую величину, чем g.
Если во время движения системы перегрузок m снять при помощи кольцевой платформы Е, то движущая сила становится равной нулю и равноускоренное движение переходит в равномерное, совершающееся по инерции с той же скоростью, которую система имела в момент снятия перегрузка.
Измерения и обработка результатов
1. Проверка формулы пути
1. На груз М2 положить добавочный груз m2 = 10,3 г.
2. Сплошную платформу F установить на некотором расстоянии S от нижнего основания груза М2.
3. Вывести грузы из состояния покоя и одновременно включить секундомер. Секундомер остановить в момент удара груза (М2 + m2) о сплошную платформу F. Показания секундомера дают время движения t.
Для выбранного расстояния S от платформы F определить время падения груза (М2 + m2) не менее трех раз и подсчитать среднее арифметическое значение <t>.
4. Аналогичные измерения выполнить для двух других расстояний S от платформы F, каждый раз определяя < t >.
5. Результаты измерений занести в журнал наблюдений 1 и вычислить ускорения для каждого случая по формулам:
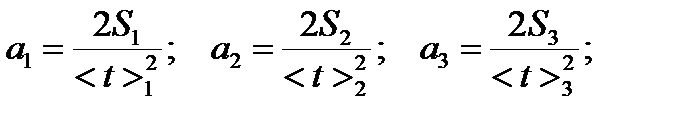
при одном и том же перегрузке m. Ускорения при разных положениях платформы F должны быть приблизительно одинаковыми.
6. Вычислить погрешности измерений (по приведенному алгоритму).
Журнал наблюдений 1
| № опыта | .m2, кг | S, м | t, c | <t>, c | a= 2S/ <t>2, м/с2 |
| 10,3•10-3 | |||||
Расчет погрешностей измерений:
1). Расчет погрешности измерения пути
1.1. S1 = ____; S2 = ____; S3 = ____.
1.2 <S> = (S1 + S2 + S3)/3 = ______________.
1.3. Δ S1 = <S> - S1 = __________________
Δ S2 = <S> - S2 = __________________
Δ S3 = <S> - S3 = __________________
1.4. (Δ S1)2= ____; (Δ S2)2= ____; (Δ S3)2= ____ .
1.5. 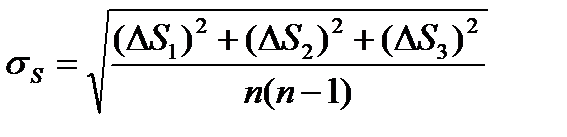 =___________ .
=___________ .
1.6. tm = ____.
1.7. Δ S = . tm σs = _____________________.
1.8.(Δ Sпр)2 = ____.
1.9. Т.к. Δ S >> Δ Sпр, то Δ S = _________.
1.10. S = <S> ± Δ S = __________.
1.11. δ = (Δ S/ <S>)•100% = ________________.
2). Расчет погрешности измерения времени
2.1. t1 = ____; . t2 = ____; t3 = ____.
2.2. <t> = (t1 + t2 + t3)/3 = _______________.
2.3. Δ t1 = <t> - t1 = ____________________
Δ t2 = <t> - t2 = ____________________
Δ t3 = <t> - t3 = ____________________.
2.4. ( Δ t1)2 = ____; ( Δ t2)2 = ____; ( Δ t3)2 = ____.
2.5. 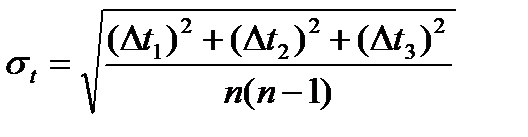 = _______________.
= _______________.
2.6. tm = ____. 2.7. Δ t = tm• σt = __________.
2.8. Δ tпр = ____<< Δ t = ____.
2.9. t = <t> ± Δ t = _________.
2.10. δ = (Δ t/<t>)•100% = ______________.
3). Расчет погрешности вычисления ускорения
3.1. Наиболее вероятное значение a: a = 2<S>/(<t>)2= ________ .
3.2. Находим частные производные: ða/ðs = 2/t2; ða/ðt = - 4 S/t3.
3.4. Абсолютная погрешность: 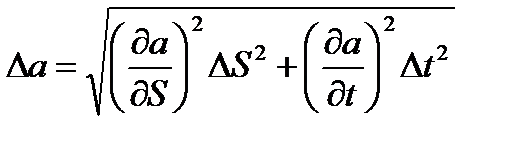 = =_________________________.
= =_________________________.
3.5. <a> = (a1 + a2 + a3)/3 = ____________________.
3.6. Окончательный результат: a = <a> ± Δa = ______________.
3.7. Относительная погрешность: δ = (Δa/<a>) •100% =__________.
2. Проверка формулы скорости
1. На груз М2 положить перегрузок m2 = 10,3 г и удерживать систему в состоянии покоя. Несколько ниже груза М2 поместить кольцевую платформу Е, а еще ниже – сплошную платформу F. Вывести систему из состояния покоя и одновременно включить секундомер.
2. Измерить время t от момента начала движения грузов до снятия перегрузка кольцевой платформой Е.
3. Измерить время t1 от момента снятия перегрузка до момента удара о сплошную платформу.
4. Измерить расстояние l между платформами.
5. Опыт повторить 3 раза, изменяя расстояния между платформами E и F.
6. Разделив расстояния l1, l2 и l3, проходимые грузом по инерции (они будут равны расстояниям между платформами за вычетом высоты груза М2), на соответствующие промежутки времени и взяв среднее арифметическое трех полученных результатов, определить скорость движения по инерции, а следовательно, и мгновенную скорость в конце равноускоренного движения. Высоту груза М2 нужно измерить штангенциркулем. Эту высоту h необходимо учитывать, так как перегрузок m снимается с верхнего основания груза М2 , а ударяется груз о сплошную платформу своим нижним основанием.
7. Результаты измерений и подсчетов заносятся в журнал наблюдений 2.
8. Значения ускорений, т.е. отношения мгновенных скоростей к соответствующим промежуткам времени равноускоренного движения (см. столбец 10 журнала наблюдений 2), приблизительно должны совпадать со значениями ускорений, полученными в первой части работы (см. столбец 6 журнала наблюдений 1).
Журнал наблюдений 2
| № опыта | t, c | <t>, c | l, м | h, м | t1, c | <t1>,c | 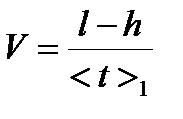 , м/c , м/c | 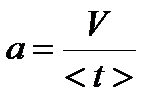 , м/с2 , м/с2 |
.3. Проверка второго закона Ньютона
1. На груз М2 положить перегрузок m2= 10,3 г, а на груз М1 перегрузок m1= 7,8 г, тогда масса, обуславливающая действующую силу будет равна разности масс перегрузков: Δm1 = m2- m1= 2,5 г, а масса системы будет равна сумме масс основных грузов и перегрузков, т.е. (2М + m1+ m2).
2. Измерить время, за которое система грузов пройдет некоторый путь за счет избыточной массы Δm = m1+ m2 = 18,1 г, занести данные наблюдения в журнал наблюдений 3.
3. Оба перегрузка переложить на груз М2, в результате чего избыточная масса будет Δm = 18,1 г, а масса системы не изменится. Измерить время, за которое система пройдет этот же путь. Подсчитав все ускорения, приобретенные под действием различных сил, убедиться что ускорения пропорциональны действующим силам:
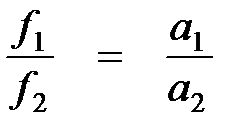
| № опыта | f•10-3, Н | t, c | S, м | a, м/с2 | а1 / а2 | f1 / f2 |
| f 1 = (m2 – m1)g= =24,53 | ||||||
| f 2 = (m1 + m2)g= =177,56 |
Журнал наблюдений 3
Контрольные вопросы
1. Что такое мгновенная скорость?
2. Приведите определения равномерного и равноускоренного движений.
3. Приведите формулы закона скоростей и закона путей при равноускоренном движении.
4. Сформулируйте и напишите формулу второго закона Ньютона.
5. Укажите силы, действующие на грузы в приборе Атвуда.
6. Решить задачу: Через невесомый блок перекинута невесомая и нерастяжимая нить, на которой подвешены два груза массами m1 = 1 кг и
m2 = 2 кг. Определить ускорение а грузов и силу натяжения Т нити. Трением в блоке пренебречь.
Литература
1. Физический практикум: Механика и молекулярная физика / под ред. проф. В.И. Ивероновой. – М.: Наука, 1967.
2. Кортнев А.В., Рублев Ю.В., Куценко А.Н. Практикум по физике. – М.: Высш. школа, 1965.
3. Савельев И.В. Курс общей физики: В 3-х т. М.: Наука, 1982. Т.1.
4. Трофимова Т.И. Курс физики. М.: Высш. Школа, 1985.
5. Яворский Б.М., Детлаф А.А. Справочник по физике. М.: Наука, 1985.
Лабораторная работа 5
Проверка основного закона динамики вращательного движения
Выполнил студент __________________, группа __________, дата ____________.
Допуск ______________
Выполнение __________
Зачет ________________
Цель работы: Ознакомиться с основными физическими понятиями и величинами, определяющими закономерности вращательного движения, опытным путем проверить выполнение основного закона динамики вращательного движения.
Приборы и материалы
| № п\п | Наименование прибора | Цена деления | Предел измерения (хmax) | Точность отсчета (Δхпр) |
| Маятник Обербека | - | - | - | |
| Грузы | - | - | - | |
| Секундомер | ||||
| Линейка |
Теоретические сведения
Основные понятия и законы
