Изучение законов равноускоренного движения тел

Выполнил студент _________________, группа____________ дата _________.

Допуск ______________

Выполнение __________

Зачет ________________

Цели работы:

1. Проверить с помощью прибора Атвуда законы равноускоренного движения.

2. Проверить второй закон Ньютона.

Приборы и материалы

№ п\п	Наименование прибора	Цена деления	Предел измерения (хmax)	Точность отсчета (Δхпр)
	Прибор Атвуда	-	-	-
	Грузы	-	-	-
	Секундомер
	Линейка

Теоретические сведения

Основные понятия и законы

Скорость

Скорость (часто обозначается 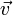, от англ. velocity или фр. vitesse) – векторная физическая величина, характеризующая быстроту перемещения и направления движения материальной точки в пространстве относительно выбранной системы отсчёта.

Вектор скорости материальной точки в каждый момент времени определяется производной по времени радиус-вектора 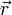этой точки:

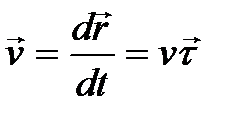(м/с),

где 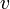— модуль скорости, 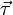— направленный вдоль скорости единичный вектор касательной к траектории в точке .

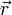Скорость направлена вдоль касательной к траектории и равна по модулю производной дуговой координаты по времени.

Если скорость тела (как векторная величина) не меняется во времени (v =const), то движение тела — равномерное (ускорение равно нулю) и тогда: скорость при равномерном движении численно равная отношению пройденного пути s к промежутку времени t, за который этот путь пройден: v = S/t.

В прямоугольной декартовой системе координат:

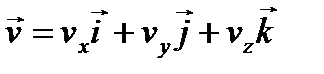
В то же время 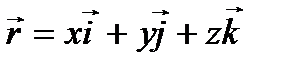, поэтому

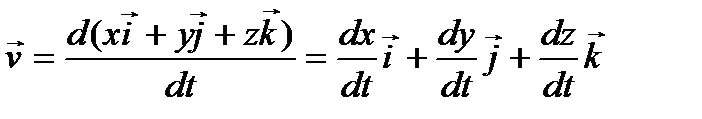
Таким образом, координаты вектора скорости – это скорости изменения соответствующей координаты материальной точки:

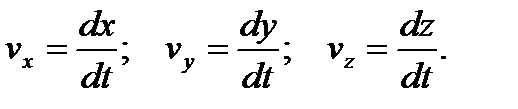
В классической механике скорость – величина относительная, т.е. преобразуется при переходе из одной инерциальной системы отсчёта в другую согласно преобразованиям Галилея.

Ускорение

Ускорение (обычно обозначается 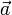, в теоретической механике 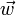) — производная скорости по времени, векторная величина, показывающая, насколько изменяется вектор скорости точки (тела) при её движении за единицу времени (т.е. ускорение учитывает не только изменение величины скорости, но и её направления).

Например, вблизи Земли падающее на Землю тело, в случае, когда можно пренебречь сопротивлением воздуха, увеличивает свою скорость примерно на 9,81 м/с каждую секунду, то есть, его ускорение равно 9,81 м/с².

Производная ускорения по времени, т.е. величина, характеризующая скорость изменения ускорения, называется рывок.

Вектор ускорения материальной точки в любой момент времени находится путём дифференцирования вектора скорости материальной точки по времени:

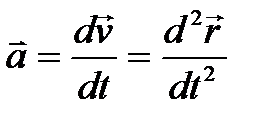, ( м/с²).

Ускорение точки при прямолинейном движении

Если вектор 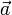не меняется со временем, движение называют равноускоренным. При равноускоренном движении справедливы формулы:

.

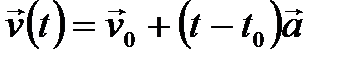
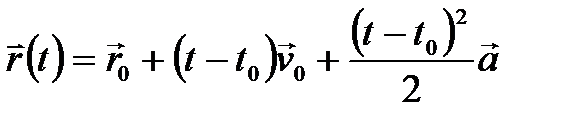Ускорение – величина абсолютная, т.е. не зависит от выбора инерциальной системы отсчета.

Законы Ньютона

Законы Ньютона — три закона, лежащие в основе классической механики и позволяющие записать уравнения движения для любой механической системы, если известны силовые взаимодействия для составляющих её тел. Впервые в полной мере сформулированы Исааком Ньютоном в книге «Математические начала натуральной философии» (1687 год). Законы Ньютона справедливы только в инерциальных системах отсчета.

Первый закон Ньютона

Первый закон Ньютона постулирует наличие такого явления, как инерция тел. Поэтому он также известен как закон инерции.

Инерция — это явление сохранения телом скорости движения (и по величине, и по направлению), когда на тело не действуют никакие силы.

Чтобы изменить скорость движения, на тело необходимо подействовать с некоторой силой. Естественно, результат действия одинаковых по величине сил на различные тела будет различным. Таким образом, говорят, что тела обладают инертностью.

Инертность — это свойство тел сопротивляться изменению их текущего состояния. Величина инертности характеризуется массой тела.

В современной физике первый закон Ньютона принято формулировать в следующем виде:

Существуют такие системы отсчёта, называемые инерциальными, относительно которых материальная точка при отсутствии внешних воздействий сохраняет величину и направление своей скорости неограниченно долго.

Закон верен также в ситуации, когда внешние воздействия присутствуют, но взаимно компенсируются (это следует из 2-го закона Ньютона, так как скомпенсированные силы сообщают телу нулевое суммарное ускорение).

Второй закон Ньютона

Второй закон Ньютона – дифференциальный закон движения, описывающий взаимосвязь между приложенной к материальной точке силой и получающимся от этого ускорением этой точки. Фактически, второй закон Ньютона вводит массу как меру проявления инертности материальной точки в выбранной инерциальной системе отсчёта (ИСО).

В инерциальной системе отсчёта ускорение, которое получает материальная точка, прямо пропорционально равнодействующей всех приложенных к ней сил и обратно пропорционально её массе.

Этот закон можно записать в виде формулы:

,

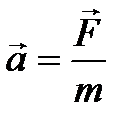где 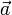– ускорение материальной точки; 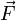– сила, приложенная к точке;
m – масса материальной точки.

В случае, когда масса материальной точки меняется со временем, второй закон Ньютона формулируется с использованием понятия импульс:

В инерциальной системе отсчета скорость изменения импульса материальной точки равна равнодействующей всех приложенных к ней сил:

,

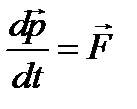где 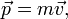– импульс точки, 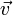– скорость точки; 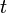– время;
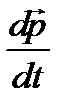– скорость изменения импульса.

Когда на тело действуют несколько сил, с учётом принципа суперпозиции второй закон Ньютона записывается:

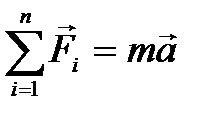
или

.

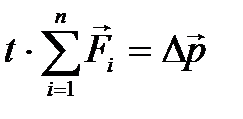Второй закон Ньютона действителен только для скоростей, много меньших скорости света и в инерциальных системах отсчёта. Для скоростей, приближенных к скорости света, используются законы теории относительности.

Третий закон Ньютона

Этот закон объясняет, что происходит с двумя взаимодействующими телами. Возьмём для примера замкнутую систему, состоящую из двух тел. Первое тело может действовать на второе с некоторой силой 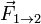, а второе – на первое с силой 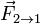. Как соотносятся силы? Третий закон Ньютона утверждает: сила действия равна по модулю и противоположна по направлению силе противодействия.

Подчеркнём, что эти силы приложены к разным телам, а потому вовсе не компенсируются.

Материальные точки попарно действуют друг на друга с силами, имеющими одинаковую природу, направленными вдоль прямой, соединяющей эти точки, равными по модулю и противоположными по направлению:

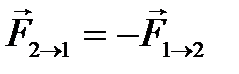
Закон отражает принцип парного взаимодействия. То есть все силы в природе рождаются парами.

Теория лабораторной работы

Равноускоренное движение происходит под действием постоянной силы. Основные законы, характеризующие равноускоренное движение: закон путей, выражающий зависимость между расстоянием, пройденным телом, и временем движения:

S = at²/2

и закон скоростей, связывающий скорость в данный момент со временем движения:

v = at (при нулевой начальной скорости).

Равноускоренно происходит падение тел с небольшой высоты в поле земного тяготения. Однако вследствие значительной величины ускорения силы тяжести (g = 9,81 м/с2) изучение законов равноускоренного движения свободно падающих тел затруднительно.

Специальное приспособление, называемое прибором Атвуда, позволяет наблюдать падение тел со значительно меньшим ускорением.

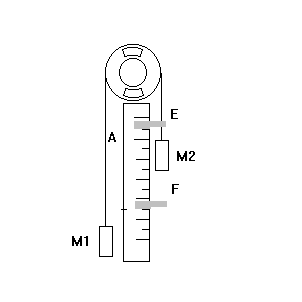
Рис. 1

Рис. 1

Устройство и принцип действия прибора Атвуда

Прибор Атвуда (рис.1) состоит из вертикальной колонки А, по всей длине которой нанесена сантиметровая шкала. На верхнем конце колонки укреплен легкий вращающийся около горизонтальной оси алюминиевый блок В (неизбежное трение на оси блока сведено до минимума). Через блок перекинута тонкая нить с двумя грузами одинаковой массы (М₁ = М₂ = M).

Если на один из грузов поместить новый груз (перегрузок) m, то вся система грузов придет в движение с некоторым ускорением а.

Вдоль колонки можно перемещать две площадки: F и E, из которых кольцевая Е служит для снятие перегрузка m, а сплошная F – для остановки движения системы. В случае необходимости кольцевая площадка Е может быть снята.

Элементарная теория прибора Атвуда выводится в предположении, что силами трения и инерцией частей прибора можно пренебречь. При этом условии движущей силой можно считать вес перегрузка m, а движущаяся масса будет складываться из массы основных грузов и массы перегрузка.

Согласно второму закону динамики можно написать:

f = mg = (2M + m)×a,

где f = mg – движущая сила, Н; (2M + m) – масса системы, кг.