Инерционный и поляризационный дрейфы
 Если частица ускоряется при сохранении условий адиабатичности, то с известным приближением к постоянно действующей силе, например, электрической, можно добавить силу инерции
Если частица ускоряется при сохранении условий адиабатичности, то с известным приближением к постоянно действующей силе, например, электрической, можно добавить силу инерции
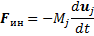 (6.59)
(6.59)
которая должна вызвать дрейф, называемый инерционным, со скоростью
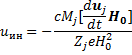 (6.60)
(6.60)
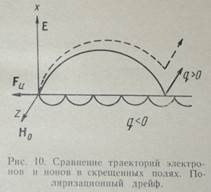
Важным частным случаем инерционного дрейфа является поляризационный, который возникает в низкочастотном электрическом поле при наличии магнитного. Низкочастотным в этом смысле полем можно считать переменное поле, рабочая частота которого ω много меньше ларморовской частоты ионов ωi. Силу инерции для переменного электрического поля (см. рис. 10) можно приближенно найти, продифференцировав по времени скорость электрического дрейфа uэ [см. выражение (6.47)] и подставив его в (6.59). Это оправданно, поскольку инерционную силу мы рассматриваем как малое возмущение в движении при постоянных полях
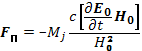 (6.61)
(6.61)
Скорость инерционного дрейфа
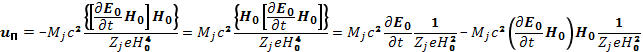 (6.62)
(6.62)
В скрещенных полях второй член обращается в нуль, и скорость поляризационного дрейфа оказывается направленной вдоль электрического поля
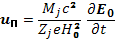 (6.63)
(6.63)
Это дрейфовое движение сопровождается необратимым отбором энергии частицей от источника, в то время как дрейф в постоянных полях происходит с периодическим поглощением и отдачей энергии. Если частицу в последнем случае каким-то образом вывести из системы полей, например на вершине циклоиды, то она будет иметь максимальную скорость движения по инерции, а через полный период обращения по ларморовской окружности скорость ее становится равной нулю.
Примером поляризационного дрейфа может служить движение частиц в замагниченной плазме при наложении переменных или импульсных электрических полей. Замагниченной называют плазму, для которой выполняются два условия:
1. 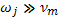 (6.64)
(6.64)
Циклотронная частота вращения частиц в магнитном поле намного превышает частоту столкновений νm частиц между собой. Это значит, что частица должна многократно обернуться по ларморовской окружности, прежде чем произойдет столкновение ее с другой частицей. При этом условии диффузия частиц поперек магнитного поля сильно затруднена. Частицы движутся, навиваясь на силовые линии магнитного поля. Только редкие столкновения «сбивают» частицы с их пути:
2. 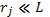 (6.65)
(6.65)
Ларморовский радиус частиц много меньше характерных размеров системы, например размеров плазменного столба, диаметра сечения потока плазмы и т. п. Наложение такого условия обеспечивает невозмущенность циклотронного вращения в ограниченном объеме..
Кроме полной замагниченности плазмы можете быть частичнаязамагниченность, когда условия (6.64) и (6.65) выполняются только для электронов. Интересно отметить, что в незамагниченнон плазме скорости электронов обычно во много раз больше скорости ионов, в частично замагничениой скорости могут выравниваться, а в полностью замагничениой скорости ионов, наоборот, намного больше электронных. Это следует из формулы (6.63), которая действительна для плазмы при наличии замагниченности тех или иных частиц. Если ноны незамагничены, то для них формула (6.63) не применима, и по ней рассчитывается движение только электронов. Для полностью замагниченной плазмы она определяет движение как ионов, так и электронов.
(источник:А.В.Чернетский, Введение в физику плазмы, гл.1, §§1.1-1.3)
Кулоновские «столкновения» в плазме. Сечение кулоновских «столкновений». Кулоновский логарифм. Кинетические параметры частиц плазмы: длина свободного пробега. Частоты соударений частиц плазмы. Бесстолкновительная плазма. Времена между соударениями частиц плазмы.
