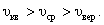Основные физические величины, использующиеся при описании явлений, происходящих в микромире

Единицы измерения физических величин при описании явлений, происходящих в микромире, подразделяются на основные и производные, которые определяются через математическую запись законов физики.
В связи с тем, что все физические явления происходят в пространстве и времени, за основные единицы принимают в первую очередь единицы длины и времени, к ним присоединяется единица массы. Основные единицы: длины l, времени t, массы m − получают определенную размерность. Размерности производных единиц определяются формулами, выражающими определенные физические законы.
Размеры основных физических единиц подбирают так, чтобы на практике было удобно ими пользоваться.
В системе СИ приняты следующие размерности: длины [l] = м (метр), времени [t] = с (секунда), массы [т] = кг (килограмм).
В системе СГС для основных единиц приняты следующие размерности: длины [/] = см (сантиметр), времени [t] = с (секунда) и массы [т] = г (грамм). Для описания явлений, происходящих в микромире, можно использовать обе системы единиц СИ и СГС.
Оценим порядки величин длины, времени и массы в явлениях микромира.
Кроме общепринятых международных систем единиц СИ и СГС используются также "естественные системы единиц", опирающиеся на универсальные физические константы. Эти системы единиц особенно уместны и используются в различных физических теориях. В естественной системе единиц за основные единицы приняты фундаментальные постоянные: скорость света в вакууме − с, постоянная Планка − ћ, гравитационная постоянная G_N, постоянная Больцмана − k: число Авогадро − N_A, и др. В естественной системе единиц Планка принято с = ћ = G_N = k = 1. Этой системой единиц пользуются в космологии для описания процессов, в которых одновременно существенны квантовые и гравитационные эффекты (теории Черных дыр, теории ранней Вселенной).
В естественной системе единиц решена проблема естественной единицы длины. Таковой можно считать комптоновскую длину волны λ₀, которая определяется массой частицы М: λ₀ = ћ/Мс.
Длина характеризует размер объекта. Так, для электрона классический радиус r₀ = e²/m_ec² = 2.81794·10^-13 см (е, m_е − заряд и масса электрона). Классический радиус электрона имеет смысл радиуса заряженного шара с зарядом е (распределение сферически симметрично), при котором энергия электростатического поля шара ε = γе²/r₀ равна энергии покоя электрона m_ec²(используется при рассмотрении томпсоновского рассеяния света).
Используется также радиус боровской орбиты. Он определяется как расстояние от ядра, на котором с наибольшей вероятностью можно обнаружить электрон в невозбужденном атоме водорода
a₀ = ћ²/m_ee² (в СГС-системе) и a₀ = (α/4π)R = 0.529·10^-10 м (в СИ-системе), α = 1/137.
Размер нуклона r ≈ 10^-13 см (1 фемтометр). Характерные размеры атомных систем − 10^-8, ядерных систем − 10^-12 ÷ 10^-13 см.
Время изменяется в широком интервале и определяется как отношение расстояния R к скорости объекта v. Для микрообъектов τ_яд = R/v = 5·10^-12 см/10⁹ см/с ~ 5·10^-22 с;
τ_{элем ч} = 10^-13 см/3·10¹⁰ см/с = 3·10^-24 с.
Массы объектов изменяются от 0 до М. Так, масса электрона m_е ≈ 10^-27 г, масса протона
m_р ≈ 10^-24 г (СГС-система). Одна атомная единица массы, использующаяся в атомной и ядерной физике, 1 а.е.м. = М(С)/12 в единицах массы атома углерода.
К фундаментальным характеристикам микрообъектов следует отнести электрический заряд, а также характеристики, необходимые для идентификации элементарной частицы.
Электрический заряд частиц Q измеряется обычно в единицах заряда электрона. Заряд электрона е = 1.6·10^-19 кулон. Для частиц в свободном состоянии Q/e = ±1, 0, а для кварков, входящих в состав адронов, Q/e = ±2/3 и ±1/3.
В ядрах заряд определяется количеством протонов Z, содержащихся в ядре. Заряд протона по абсолютной величине равен заряду электрона.
Для идентификации элементарной частицы необходимо знать:
I − изотопический спин;
J − собственный момент количества движения − спин;
Р − пространственную четность;
С − зарядовую четность;
G − G-четность.
Эти сведения записываются в виде формулы I^G(J^PC).
Спин − одна из важнейших характеристик частицы, для измерения которой используется фундаментальная константа Планка h или ћ = h/2π = 1.0544·10^-27 [эрг-с]. Бозоны имеют целый спин в единицах ћ: (0,1, 2,...)ћ, фермионы − полуцелый (1/2, 3/2,.. .)ћ. В классе суперсимметричных частиц значения спинов фермионов и бозонов меняются местами.

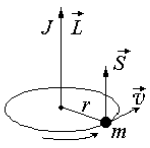Рис- 4. Классическое представление момента количества движения J.

Рис. 4 иллюстрирует физический смысл спина J по аналогии с классическим представлением о моменте количества движения частицы с массой m = 1 г, движущейся со скоростью v = 1 см/с по окружности с радиусом r = 1 см. В классической физике момент количества движения J = mvr = L (L − орбитальный момент). В квантовой механике J = [ 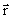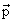] = 10²⁷ћ = 1 эрг·с для тех же параметров движущегося по окружности объекта, где ћ = 1.05·10^-27 эрг·с.
Проекция спина элементарной частицы на направление ее импульса называется спиральностью. Спиральность безмассовой частицы с произвольным спином принимает только два значения: по или против направления импульса частицы. Для фотона возможные значения спиральности равны ±1, для безмассового нейтрино спиральность равна ±1/2.
Спиновый момент количества движения атомного ядра определяется как векторная сумма спинов элементарных частиц, образующих квантовую систему, и орбитальных моментов этих частиц, обусловленных их движением внутри системы. Орбитальный момент | 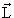|, и спиновый момент | 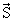| приобретают дискретное значение. Орбитальный момент | 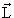| = ћ[l(l +1)]^1/2, где l − орбитальное квантовое число (может принимать значения 0, 1,2,...), собственный момент количества движения | 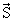| = ћ[s(s + 1)]^1/2 где s − спиновое квантовое число (может принимать нулевые, целые или полуцелые значенияJ, полный момент количества движения равен сумме + = .
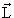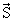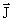К производным единицам следует отнести: энергию частицы, быстроту, заменяющую скорость для релятивистских частиц, магнитный момент и др.
Энергия покоящейся частицы: Е = mc²; движущейся частицы: Е = m²c⁴ + p²c².
Для нерелятивистских частиц: Е = mс² + р²/2m; для релятивистских частиц, с массой m = 0: Е = ср.
Единицы измерения энергии − эВ, кэВ, МэВ, ГэВ, ТэВ, ... 1 ГэВ = 10⁹ эВ, 1 ТэВ = 10¹² эВ,
1 эВ = 1.6·10^-12 эрг.
Скорость частицы β = v/c, где с = 3·10¹⁰ см/с − скорость света. Скорость частицы определяет такую важнейшую характеристику как Лоренц-фактор частицы γ = 1/(1-β²)^1/2 = E/mc². Всегда γ > 1- Для нерелятивистских частиц 1 < γ < 2, а для релятивистских частиц γ > 2.
В физике высоких энергий скорость частицы β близка к 1 и для релятивистских частиц ее трудно определить. Поэтому вместо скорости используется быстрота y, которая связана со скоростью соотношением у = (1/2)ln[(1+β)/(1-β)] = (1/2)ln[(E+p)/(E-p)]. Быстрота изменяется от 0 до ∞.

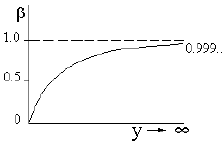Рис. 5. Функциональная связь между скоростью частицы β и быстротой у.

Функциональная связь между скоростью частицы и быстротой показана на рис. 5. Для релятивистских частиц при β → 1, Е → р, тогда вместо быстроты можно использовать псевдобыстроту η, которая определяется углом вылета частицы θ, η = (1/2)ln tan(θ/2). В отличие от скорости быстрота − аддитивная величина, т.е. у₂ = y₀ + y₁ для любой системы отсчета и для любых релятивистских и нерелятивистских частиц.
Магнитный момент μ = Iπr²/c, где ток I = ev/2πr, возникает из-за вращения электрического заряда. Таким образом, любая заряженная частица имеет магнитный момент. При рассмотрении магнитного момента электрона используется магнетон Бора
μ_B = eћ/2m_ec = 0.5788·10^-14 МэВ/Гс, магнитный момент электрона 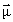= g·μ_B· 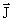. Коэффициент g называется гиромагнитным отношением. Для электрона g = 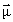/μ_B· 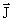= 2, т.к. J = ћ/2, 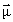= μ_B при условии, что электрон − точечная бесструктурная частица. Гиромагнитное отношение g содержит информацию о структуре частицы. Величина (g − 2) измеряется в экспериментах, направленных на изучение структуры частиц, отличных от лептонов. Для лептонов эта величина свидетельствует о роли более высоких электромагнитных поправок (см. далее п. 7.1).
В ядерной физике используется ядерный магнетон μ_я = eћ/2m_pc, где m_p − масса протона.

Вопрос №56

Глюо́ны (от англ. gluon, от glue — клей) — элементарные частицы, переносчики сильного взаимодействия^[5].

Говоря техническим языком, глюоны — это векторные калибровочные бозоны, непосредственно отвечающие за сильное цветовое взаимодействие между кварками в квантовой хромодинамике (КХД)^[5]. В отличие от фотонов в квантовой электродинамике (КЭД), которые электрически нейтральны и не взаимодействуют^[6] друг с другом, глюоны сами несут цветовой заряд и, таким образом, участвуют в сильных взаимодействиях, а не только переносят их. Это делает КХД значительно более сложной для понимания, чем КЭД.

Глюон — это квант векторного (то есть обладающего единичным спином и отрицательной внутренней чётностью) поля в КХД. Он не имеет массы. В квантовой теории поля ненарушенная калибровочная инвариантность требует, чтобы калибровочный бозон был безмассовым^[1] (эксперимент ограничивает массу глюона сверху значением не более нескольких МэВ^[2]). Все эти свойства (а также нулевой электрический заряд) сближают его с фотоном.

В то время как массивные векторные частицы имеют три состояния поляризации, безмассовые векторные калибровочные бозоны, такие, как глюон и фотон, имеют только две возможных поляризации из-за того, что калибровочная инвариантность требует поперечной поляризации.

Глюон обладает нулевым изоспином. Бесцветные глюоны g3{\displaystyle g_{3}} и g8{\displaystyle g_{8}} являются античастицами самим себе, то есть истинно нейтральными частицами.

Кварк — фундаментальная частица в Стандартной модели, обладающая электрическим зарядом, кратным e/3, и не наблюдающаяся в свободном состоянии, но входящая в состав адронов (сильно взаимодействующих частиц, таких как протоны и нейтроны). Кварки являются бесструктурными, точечными частицами; это проверено вплоть до масштаба примерно 10⁻¹⁶ см^[2], что примерно в 20 тысяч раз меньше размера протона.

В настоящее время известно 6 разных «сортов» (чаще говорят — «ароматов») кварков, свойства которых даны в таблице. Кроме того, для калибровочного описания сильного взаимодействия постулируется, что кварки обладают и дополнительной внутренней характеристикой, называемой «цвет». Каждому кварку соответствует антикварк — античастица с противоположными квантовыми числами.

Гипотеза о том, что адроны построены из специфических субъединиц, была впервые выдвинута М. Гелл-Манном и, независимо от него, Дж. Цвейгом в 1964 году^[2].

Вопрос №57

Пусть идеальный газ находится в поле консервативных сил в условиях теплового равновесия. При этом концентрация газа будет различной в точках с различной потенциальной энергией, что необходимо для соблюдения условий механического равновесия. Так, число молекул в единичном объеме n убывает с удалением от поверхности Земли, и давление, в силу соотношения P = nkT, падает.

Если известно число молекул в единичном объеме, то известно и давление, и наоборот. Давление и плотность пропорциональны друг другу, поскольку температура в нашем случае постоянна. Давление с уменьшением высоты должно возрастать, потому что нижнему слою приходится выдерживать вес всех расположенных сверху атомов.

Исходя из основного уравнения молекулярно-кинетической теории: P = nkT, заменим P и P₀ в барометрической формуле (2.4.1) на n и n₀ и получим распределение Больцмана для молярной массы газа:

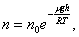(2.5.1)

где n₀ и n - число молекул в единичном объёме на высоте h = 0 и h.

Так как 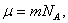а 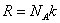, то (2.5.1) можно представить в виде

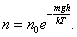(2.5.2)

С уменьшением температуры число молекул на высотах, отличных от нуля, убывает. При T = 0 тепловое движение прекращается, все молекулы расположились бы на земной поверхности. При высоких температурах, наоборот, молекулы оказываются распределёнными по высоте почти равномерно, а плотность молекул медленно убывает с высотой. Так как mgh – это потенциальная энергия U, то на разных высотах U = mgh – различна. Следовательно, (2.5.2) характеризует распределение частиц по значениям потенциальной энергии:

,

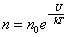(2.5.3)

– это закон распределения частиц по потенциальным энергиям – распределение Больцмана. Здесь n₀ – число молекул в единице объёма там, где U = 0.

На рисунке 2.11 показана зависимость концентрации различных газов от высоты. Видно, что число более тяжелых молекул с высотой убывает быстрее, чем легких.

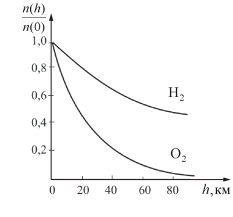
Рис. 2.11

Из (2.5.3) можно получить, что отношение концентраций молекул в точках с U₁ и i>U₂ равно:

.

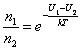(2.5.4)

Больцман доказал, что соотношение (2.5.3) справедливо не только в потенциальном поле сил гравитации, но и в любом потенциальном поле, для совокупности любых одинаковых частиц, находящихся в состоянии хаотического теплового движения.

Вопрос №58

ывод формулы функции распределения молекул по скоростям есть в учебнике Ю.И Тюрина и др. (ч. 1) или И.В. Савельева (т. 1). Мы воспользуемся результатами этого вывода.

Скорость – векторная величина. Для проекции скорости на ось х (x-й составляющей скорости) из (2.2.1) имеем

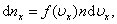тогда

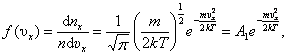(2.3.1)

где А₁ – постоянная, равная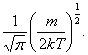

Графическое изображение функции показано на рисунке 2.2. Видно, что доля молекул со скоростью 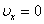не равна нулю. При 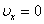, 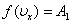(в этом физический смысл постоянной А1).

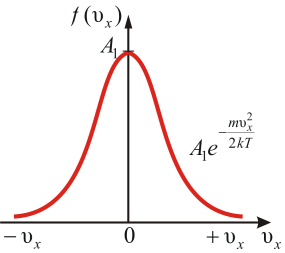
Рис. 2.2

Приведённое выражение и график справедливы для распределения молекул газа по x-компонентам скорости. Очевидно, что и по y- и z-компонентам скорости также можно получить:

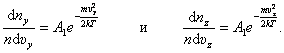Вероятность того, что скорость молекулы одновременно удовлетворяет трём условиям: x-компонента скорости лежит в интервале от υ_х до υ_х+dυ_х; y-компонента, в интервале от υ_y до υ_y+dυ_y; z-компонента, в интервале от υ_z до υ_z+dυ_z будет равна произведению вероятностей каждого из условий (событий) в отдельности:

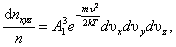где 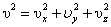, или

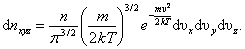(2.3.2)

Формуле (2.3.2) можно дать геометрическое истолкование: dn_xyz – это число молекул в параллелепипеде со сторонами dυ_x, dυ_y, dυ_z, то есть в объёме dV=dυ_xdυ_ydυ_z(рис. 2.3), находящемся на расстоянии 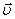от начала координат в пространстве скоростей.

Эта величина (dn_xyz) не может зависеть от направления вектора скорости 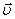. Поэтому надо получить функцию распределения молекул по скоростям независимо от их направления, то есть по абсолютному значению скорости.

Если собрать вместе все молекулы в единице объёма, скорости которых заключены в интервале от υ до υ+dυ по всем направлениям, и выпустить их, то они окажутся через одну секунду в шаровом слое толщиной dυ и радиусом υ (рис. 2.4). Этот шаровой слой складывается из тех параллелепипедов, о которых говорилось выше.

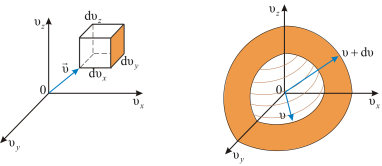	Рис. 2.3	Рис. 2.4

Объём этого шарового слоя

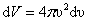Общее число молекул в слое, как следует из (2.3.2)

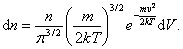Отсюда следует закон распределения молекул по абсолютным значениям скоростей Максвелла:

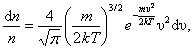(2.3.3)

где 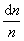– доля всех частиц в шаровом слое объема dV, скорости которых лежат в интервале от υ до υ+dυ.

При dυ = 1 получаем плотность вероятности, или функцию распределения молекул по скоростям:

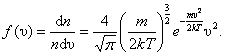(2.3.4)

Эта функция обозначает долю молекул единичного объёма газа, абсолютные скорости которых заключены в единичном интервале скоростей, включающем данную скорость.

Обозначим: 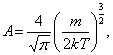тогда из (2.3.4) получим:

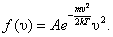(2.3.5)

График этой функции показан на рисунке 2.5.

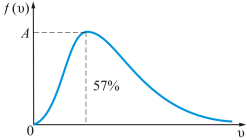
Рис. 2.5

Выводы:

• Вид распределения молекул газа по скоростям для каждого газа зависит от рода газа (m) и от параметра состояния (Т). Давление P и объём газа V на распределение молекул не влияют.
• В показателе 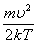степени стоит отношение , т.е. кинетической энергии, соответствующей данной скорости υ к (kТ) – средней энергии теплового движения молекул при данной температуре, значит распределение Максвелла характеризует распределение молекул по значениям кинетической энергии (то есть показывает, какова вероятность при данной температуре иметь именно такое значение кинетической энергии).

Рассмотрим пределы применимости классического описания распределения частиц по скоростям. Для этого воспользуемся соотношением неопределенностей Гейзенберга. Согласно этому соотношению координаты и импульс частицы не могут одновременно иметь определенное значение. Классическое описание возможно, если выполнены условия: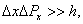

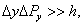
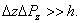
Здесь 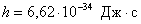– постоянная Планка – фундаментальная константа, определяющая масштаб квантовых (микроскопических) процессов.

Таким образом, если частица находится в объеме 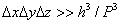, то в этом случае возможно описание ее движения на основе законов классической механики.

Наиболее вероятная, среднеквадратичная и средняя арифметическая скорости молекул газа

Рассмотрим, как изменяется с абсолютной величиной скорости число частиц, приходящихся на единичный интервал скоростей, при единичной концентрации частиц.

График функции распределения Максвелла

,

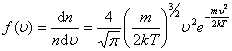приведен на рисунке 2.6.

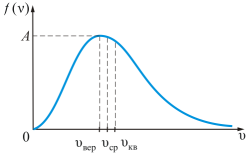
Рис. 2.6

Из графика видно, что при «малых» υ, т.е. при 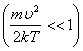, имеем 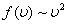; затем 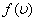достигает максимума А и далее экспоненциально спадает .

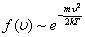Величину скорости, на которую приходится максимум зависимости 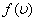, называют наиболее вероятной скоростью.

Найдем эту скорость из условия равенства производной .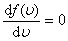

,

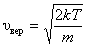(2.3.6)

– наиболее вероятная скорость одной молекулы.

Для одного моля газа:

.

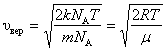(2.3.7)

Среднюю квадратичную скорость найдем, используя соотношение :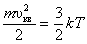

.

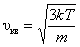– для одной молекулы;

(2.3.8)

.

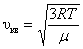– для одного моля газа.

(2.3.9)

Средняя арифметическая скорость:

.

.

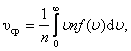где 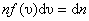– число молекул со скоростью от υ до υ+dυ. Если подставить сюда f(υ) и вычислить, то получим:

.

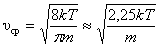– для одной молекулы;

(2.3.10)

.

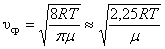– для одного моля газа.

(2.3.11)

Все три скорости незначительно отличаются друг от друга множителем порядка единицы, причем