Вращательное движение твердого тела.
ОПРЕДЕЛЕНИЕ: Вращательным движением твердого тела будем называть такое движение, при котором все точки тела движутся по окружностям, центры которых лежат на одной и ой же прямой, называемой осью вращения.
Для изучения динамики вращательного к известным кинематическим величинам добавляются ещё две величины: момент силы (M) и момент инерции (J).
1. Из опыта известно: ускорение вращательного движения зависит не только от величины силы, действующей на тело, но и от расстояния от оси вращения до линии, вдоль которой действует сила. Для характеристики этого обстоятельства вводится физическая величина называемая моментом силы.
Рассмотрим простейший случай.
 ОПРЕДЕЛЕНИЕ: Моментом силы
ОПРЕДЕЛЕНИЕ: Моментом силы 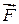 относительно некоторой точки “O” называется векторная величина
относительно некоторой точки “O” называется векторная величина 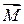 , определяемая выражением
, определяемая выражением 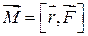 , где
, где 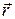 – радиус-вектор, проведенный из точки “O” в точку приложения силы.
– радиус-вектор, проведенный из точки “O” в точку приложения силы.
Из определения следует, что 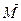 является аксиальным вектором. Его направление выбрано так, что вращение вектора вокруг точки “O” в направлении силы и вектор
является аксиальным вектором. Его направление выбрано так, что вращение вектора вокруг точки “O” в направлении силы и вектор 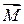 образуют правовинтовую систему. Модуль момента силы равен
образуют правовинтовую систему. Модуль момента силы равен 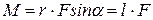 , где a – угол между направлениями векторов
, где a – угол между направлениями векторов 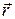 и
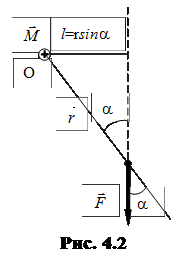
и 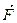 , а l = r·sina – длина перпендикуляра, опущенного из точки “O” на прямую, вдоль которой действует сила (называется плечом силы относительно точки “O”) (рис. 4.2).
, а l = r·sina – длина перпендикуляра, опущенного из точки “O” на прямую, вдоль которой действует сила (называется плечом силы относительно точки “O”) (рис. 4.2).
2. Опытные данные свидетельствуют, что на величину углового ускорения оказывает влияние не только масса вращающегося тела, но и распределение массы относительно оси вращения. Величина, учитывающая это обстоятельство, носит название момента инерции относительно оси вращения.
ОПРЕДЕЛЕНИЕ: Строго говоря, моментом инерции тела относительно некоторой оси вращения называется величина J, равная сумме произведений элементарных масс на квадраты их расстояний от данной оси 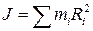 .
.
Суммирование проводится по всем элементарным массам, на которые было разбито тело. Следует иметь ввиду, что эта величина (J) существует безотносительно к вращению (хотя понятие момента инерции было введено при рассмотрении вращения твердого тела).
Каждое тело независимо от того покоится оно или вращается обладает определенным моментом инерции относительно любой оси, подобно тому как тело обладает массой независимо от того движется оно или покоится.
Учитывая, что 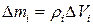 , момент инерции можно представить в виде:
, момент инерции можно представить в виде: 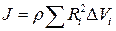 . Это соотношение приближенно и оно будет тем точнее, чем меньше элементарные объемы и соответствующие им элементы массы. Следовательно, задача нахождения моментов инерции сводится к интегрированию:
. Это соотношение приближенно и оно будет тем точнее, чем меньше элементарные объемы и соответствующие им элементы массы. Следовательно, задача нахождения моментов инерции сводится к интегрированию: 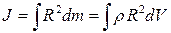 . Здесь интегрирование проводится по всему объему тела.
. Здесь интегрирование проводится по всему объему тела.
Запишем моменты инерции некоторых тел правильной геометрической формы.
| 1. Однородный длинный стержень. | |
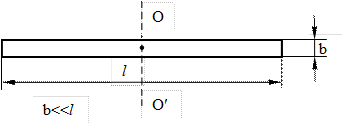 Рис. 4.3 Рис. 4.3 | Момент инерции относительно оси, перпендикулярной к стержню и проходящей через его середину равен 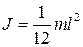 |
| 2. Сплошной цилиндр или диск. | |
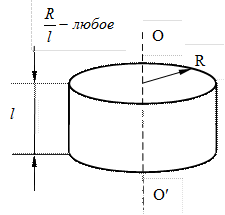 Рис. 4.4 Рис. 4.4 | Момент инерции относительно оси, совпадающей с геометрической осью, равен 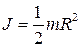 . . |
| 3. Тонкостенный цилиндр радиуса R. | |
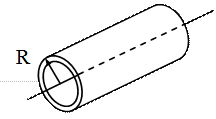 Рис. 4.5 Рис. 4.5 | 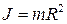 |
| 4. Момент инерции шара радиуса R относительно оси, проходящей через его центр | |
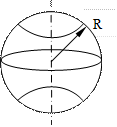 Рис. 4.6 Рис. 4.6 | 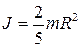 |
| 5. Момент инерции тонкого диска (толщина b<<R) относительно оси, совпадающей с диаметром диска. | |
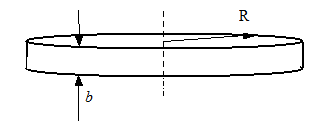 Рис. 4.7 Рис. 4.7 | 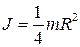 |
| 6. Момент инерции бруска | |
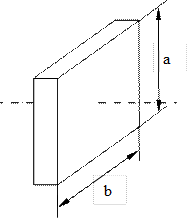 Рис. 4.8 Рис. 4.8 | 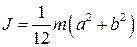 |
| 7. Момент инерции кольца | |
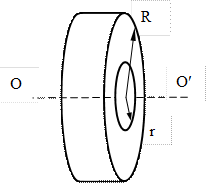 Рис. 4.9 Рис. 4.9 | 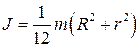 |
 Вычисления момента инерции здесь достаточно просты, т.к. тело предполагаем однородным и симметричным, а момент инерции определяем относительно оси симметрии.
Вычисления момента инерции здесь достаточно просты, т.к. тело предполагаем однородным и симметричным, а момент инерции определяем относительно оси симметрии.
Для определения момента инерции тела относительно любой оси необходимо воспользоваться теоремой Штейнера.
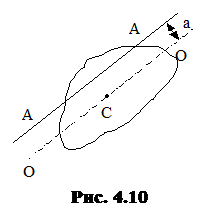
ОПРЕДЕЛЕНИЕ: Момент инерции J относительно произвольной оси равен сумме момента инерции Jс относительно оси, параллельной данной и проходящей через центр инерции тела, и произведения массы тела на квадрат расстояния между осями (рис. 4.10):
J = Jc + ma2.
Момент импульса тела.
Для описания вращательного движения потребуется ещё одна величина 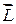 , называемая моментом импульса.
, называемая моментом импульса.
Сначала определим момент импульса материальной точки.
ОПРЕДЕЛЕНИЕ: Момент импульса материальной точки вводится аналогично моменту силы. Момент импульса 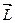 относительно точки О называется векторная величина, определяемая выражением:
относительно точки О называется векторная величина, определяемая выражением: 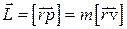 ,
,
 где
где 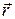 – радиус-вектор, проведенный из точки “O” в ту точку пространства, в которой находится материальная точка,
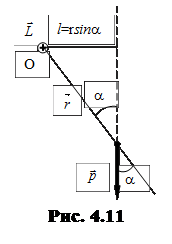
– радиус-вектор, проведенный из точки “O” в ту точку пространства, в которой находится материальная точка, 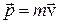 . Вводя плечо l = r·sina, модуль вектора
. Вводя плечо l = r·sina, модуль вектора 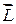 можно записать в виде
можно записать в виде 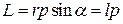 (рис. 4.11).
(рис. 4.11). 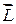 – это векторная величина (псевдовектор). Вектор
– это векторная величина (псевдовектор). Вектор 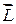 направлен по оси вращения в ту сторону, куда перемещается острие буравчика при вращении рукоятки буравчика по направлению вращения тела. Если рассматривать
направлен по оси вращения в ту сторону, куда перемещается острие буравчика при вращении рукоятки буравчика по направлению вращения тела. Если рассматривать 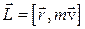 как векторное произведение
как векторное произведение 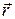 и
и 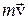 , то направление вектора
, то направление вектора 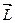 будет перпендикулярно плоскости, где лежат вектора
будет перпендикулярно плоскости, где лежат вектора 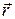 и
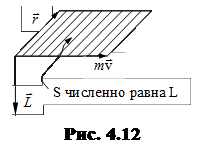
и 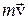 . L – численно равен площади параллелограмма, построенного на r и mv (рис. 4.12).
. L – численно равен площади параллелограмма, построенного на r и mv (рис. 4.12).
Выясним, чем определяется изменением момента импульса со временем. Продифференцируем выражение 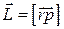 по времени “t”. Получим
по времени “t”. Получим
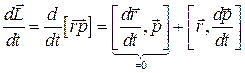 ;
;
Первое слагаемое равно «0», т.к. представляет векторное произведение векторов одинакового направления. В самом деле 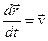 и следовательно совпадает с вектором
и следовательно совпадает с вектором 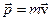 по направлению. Во втором слагаемом вектор
по направлению. Во втором слагаемом вектор 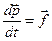 – действующая на тело сила (по II-закону Ньютона). Следовательно,
– действующая на тело сила (по II-закону Ньютона). Следовательно,

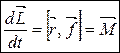 , (4.1)
, (4.1)
где 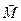 – момент приложенных к материальной точке сил, взятый относительно той же точки «О», относительно которой берется момент импульса
– момент приложенных к материальной точке сил, взятый относительно той же точки «О», относительно которой берется момент импульса 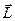 .
.
Отсюда следует формулировка закона сохранения момента импульса.
 ОПРЕДЕЛЕНИЕ: Если результирующий момент действующих на материальную точку сил относительно какой-либо точки «О» равен нулю, то момент импульса материальной точки, взятый относительно той же точки «О» будет оставаться постоянным.
ОПРЕДЕЛЕНИЕ: Если результирующий момент действующих на материальную точку сил относительно какой-либо точки «О» равен нулю, то момент импульса материальной точки, взятый относительно той же точки «О» будет оставаться постоянным.
Если сравнивать выражение 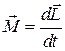 с выражением II закона Ньютона
с выражением II закона Ньютона 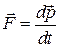 , то видно, что для вращательного движения используется вместо силы
, то видно, что для вращательного движения используется вместо силы 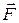 момент силы
момент силы 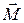 , а вместо импульса
, а вместо импульса 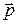 момент импульса
момент импульса 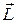 .
.
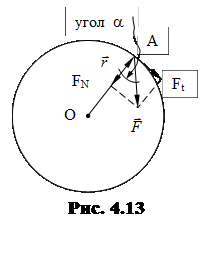
Скалярное выражение для момента силы можно получить более просто. Нормальная составляющая силы не влияет на величину скорости и уравновешивается силой реакции связи рис. 4.13. Тангенциальная составляющая силы Ft изменяет v, тогда по II закону Ньютона
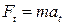 ;
; 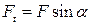 ;
; 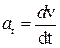 .
.
Следовательно, 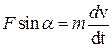 .
.
Умножая обе части уравнения на r, получим
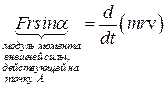
Вводя величину 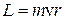 , получаем, что
, получаем, что
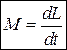 . (4.2)
. (4.2)
Формула для момента силы 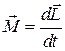 справедлива не только для материальной точки, но и для любого тела, если его рассматривать как совокупность материальных точек.
справедлива не только для материальной точки, но и для любого тела, если его рассматривать как совокупность материальных точек.
Рассмотрим систему из N материальных точек. Разобьем силы на внутренние и внешние. Результирующий момент внутренних сил, действующих на i-ую материальную точку, обозначим 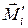 , а результирующий момент внешних сил, действующих на ту же точку
, а результирующий момент внешних сил, действующих на ту же точку 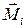 . Тогда для i-ой материальной точки можно записать
. Тогда для i-ой материальной точки можно записать
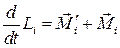 ,
,
где i=1, 2, 3,…, N
Сложим эти уравнения
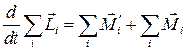 .
.
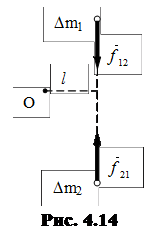 Величина
Величина 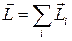 называется моментом импульса системы материальных точек.
называется моментом импульса системы материальных точек.
Первая сумма – сумма моментов внутренних сил равна «0».
ПОЯСНЕНИЕ: Рассмотрим две любые элементарные массы Dm1 и Dm2. Силы, с которыми они взаимодействуют, лежат на одной прямой (рис. 4.14). Их моменты относительно произвольной точки “O” равны по величине и противоположны по направлению. Поэтому моменты внутренних сил попарно уравновешивают друг друга и сумма моментов всех внутренних сил для любой системы материальных точек, в частности для твердого тела, всегда равна нулю. Это утверждение справедливо как для суммарного момента всех внутренних сил, взятого относительно любой точки, так и для суммарного момента этих сил, взятого относительно любой оси.
Вторая сумма – суммарный момент внешних сил равен 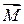 , т.е.
, т.е. 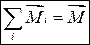 .
.
Тогда 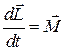 (здесь
(здесь 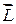 и
и 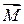 относятся к системе материальных точек).
относятся к системе материальных точек).
Для замкнутой системы материальных точек 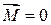 , вследствие чего суммарный момент импульса
, вследствие чего суммарный момент импульса 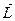 не зависит от времени.
не зависит от времени.
| ЛЕКЦИЯ 6 |
