Раздел 5. Волновая оптика. КВАНТОВАЯ ФИЗИКА

Волновые свойства света

· Скорость света в среде:

,

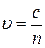где с – скорость света в вакууме; n – абсолютный показатель преломления среды.

· Оптическая длина пути световой волны:

,

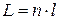где l – геометрическая длина пути световой волны в среде с показателем преломления n. Если показатель преломления непостоянный по длине геометрического пути ( 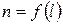), то .

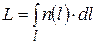· Оптическаяразность хода двух световых лучей – это разность длин оптических путей:

.

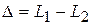· Связь разности фаз волн 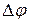и оптической разности хода лучей :

.

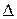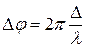· Условие максимума при интерференции:

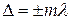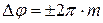, или , где .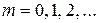

· Условие минимума при интерференции:

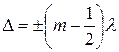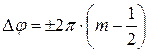, или , где .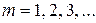

· Расстояние от m-ой светлой полосы до нулевой полосы в опыте Юнга (рис. 5.1):

,

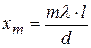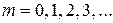
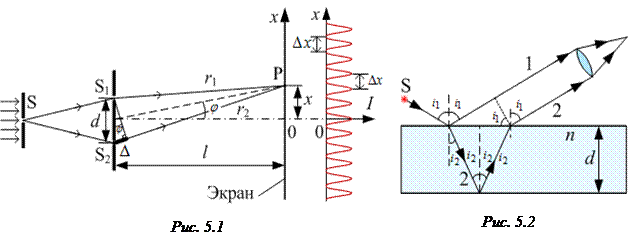· Расстояние от m-ой тёмной полосы до нулевой в опыте Юнга (рис. 5.1):

, .

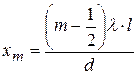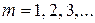· Расстояние 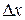между центрами соседних максимумов в опыте Юнга (рис. 5.1):

.

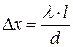· Оптическая разность хода световых волн, отраженных от верхней и нижней поверхностей тонкой плоскопараллельной пластинки или пленки, находящейся в воздухе (рис. 5.2):

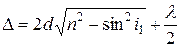, или ,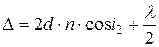

где d – толщина пластинки (плёнки); 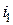– угол падения; 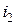– угол преломления. Второе слагаемое в формулах учитывает изменение оптической длины пути световой волны на 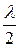при отражении её от оптически более плотной среды («потеря пол-волны»).

· Радиусы темных колец Ньютона в отраженном свете (или светлых в проходящем свете)

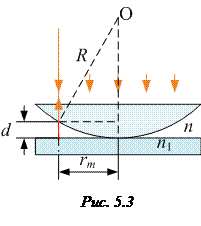
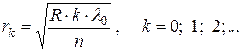
Здесь k – номер кольца; R – радиус кривизны линзы (рис. 5.3); n – показатель преломления среды в зазоре между линзой и пластинкой.

· Радиусы светлых колец Ньютона в отраженном свете (или тёмных в проходящем свете)

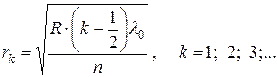
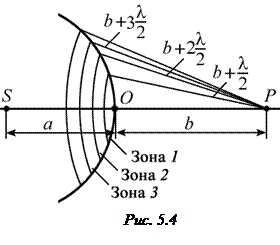Здесь k – номер кольца; R – радиус кривизны линзы (рис. 5.3); n – показатель преломления среды в зазоре между линзой и пластинкой.

· Радиус зоны Френеля с номером k (рис.5.4):

,

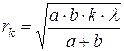где a – расстояние диафрагмы с круглым отверстием от точечного источника света; b – расстояние диафрагмы от экрана, на котором ведется наблюдение дифракционной картины; λ – длина волны. Условие максимума интенсивности в точке наблюдения Р при дифракции на круглом отверстии: число зон Френеля k, укладывающихся в отверстии, нечётно. Условие минимума: число зон чётно. Для плоской волны (при 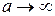) радиус k-ой зоны:

.

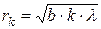· Дифракция света на одиночной щели шириной а при нормальном падении лучей.

- Условиеминимума:

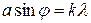; k=±1, ±2, ±3… .

- Приблизительное условиемаксимума:

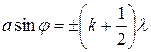; k=1, 2, 3… .

- Более точное условиемаксимума:

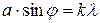; k=0; ±1.43, ±2.46, ±3.47, … .

Здесь φ – угол дифракции; k – номер максимума или минимума.

· Дифракция света на дифракционной решётке при нормальном падении лучей.

- Условие главных максимумов:

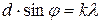; k=0, ±1, ±2, ±3….

- Условиеглавных минимумов

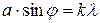; k=±1, ±2, ±3… .

Здесь φ – угол дифракции; k – номер максимума или минимума; а – ширина щели; d – период (постоянная) решётки.

· Закон Малюса. Интенсивность I прошедшей через анализатор волны (рис. 5.5):

,

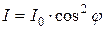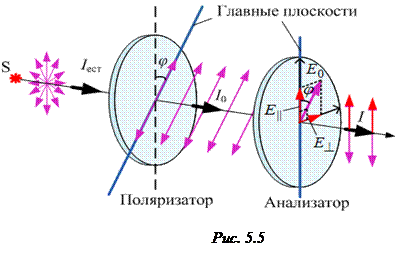где I₀ – интенсивность падающей на анализатор линейно поляризованной волны, φ – угол между главной плоскостью анализатора и плоскостью колебаний падающей на анализатор волны (или угол между главными плоскостями поляризатора и анализатора). При прохождении естественного (неполяризованного) света через идеальный (непоглощающий) поляризатор его интенсивность ослабляется в 2 раза (см. рис. 5.5):

.

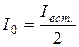С учётом поглощения света поляризатором и анализатором:

, ,

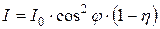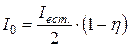где 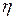– доля поглощаемого светового потока.

Квантовые свойства света

· Полная энергетическая светимость (интегральная интенсивность теплового излучения)R_T численно равна энергии всех длин волн, излучаемой за единицу времени с единичной площади поверхности нагретого тела:

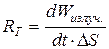, или ,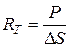

где 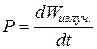– мощность излучения (световой поток).

· Спектральная плотность энергетической светимости(монохроматическая интенсивность излучения) численно равна энергии, излучаемой за единицу времени с единичной площади поверхности тела в расчёте на единичный интервал длин волн вблизи заданной длины волны:

.

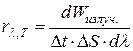· Спектральная поглощательная способность тела – это величина, показывающая, какую долю энергии падающего излучения в интервале длин волн [l; l+dl] вблизи данной длины волны l тело поглощает:

.

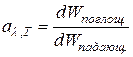Для абсолютно черного тела .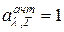

· Закон Кирхгофа: отношение монохроматической интенсивности излучения к поглощательной способности тела не зависит от природы тела; является универсальной (одинаковой для всех тел) функцией длины волны и температуры(универсальная функция Кирхгофа ):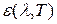

.

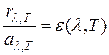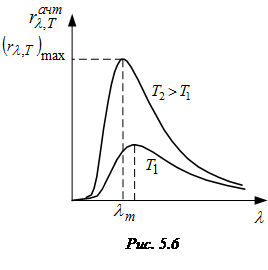
Для абсолютно чёрного тела (рис. 5.6):

.

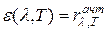· Первый закон Вина (закон смещения Вина). Длина волны λ_m, на которую приходится максимум монохроматической интенсивности излучения абсолютно чёрного тела, обратно пропорциональна абсолютной температуре (см. рис.5.6):

.

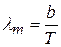Здесь 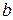– первая константа Вина.

· Второй закон Вина:максимальное значение спектральной плотности энергетической светимости абсолютно чёрного тела прямо пропорционально пятой степени абсолютной температуры (см. рис. 5.6):

.

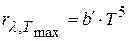Здесь 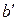– вторая константа Вина.

· Закон Стефана-Больцмана. Полная энергетическая светимость абсолютно черного тела пропорциональна четвертой степени абсолютной температуры:

.

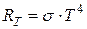Здесь 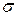– постоянная Стефана-Больцмана.

· Полнаяэнергетическая светимость серого тела

,

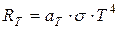где 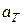– коэффициент черноты (коэффициент серости) серого тела, то есть тела, одинаково поглощающего излучение всех длин волн: 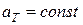для всех λ.

· Энергия фотона

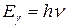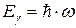, или , или .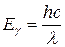

Здесь 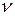– частота света; 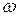– круговая частота; – длина волны света; 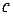– скорость света в вакууме; 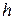– постоянная Планка; 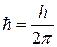– редуцированная постоянная Планка (постоянная Планка «с чертой»).

· Масса фотона

.

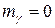· Импульс фотона

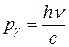, или .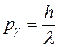

· Давление света при нормальном падении лучей

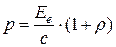, или .

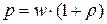Здесь 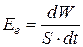– энергетическая освещённость (энергия света, попадающая на единичную площадку за единицу времени); – коэффициент отражения, равный нулю для зачернённой поверхности и единице для зеркальной; 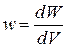– объёмная плотность энергии световой волны.

· Интенсивность света (плотность потока энергии) – это энергия световых волн, переносимая через единичную площадку, перпендикулярную лучам, за единицу времени:

.

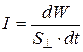· Уравнение Эйнштейна для внешнего фотоэффекта:

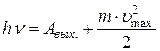, или .

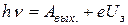Здесь 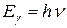– энергия фотона, падающего на поверхность металла; 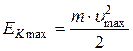– максимальная кинетическая энергия фотоэлектронов, 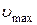– их скорость; 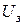– задерживающее напряжение; 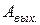– работа выхода электрона из металла.

· Красная граница фотоэффекта – это минимальная частота 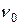или максимальная длина волны 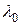, при которых ещё возможен фотоэффект:

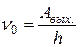, или .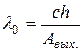

· Изменение длины волны при эффекте Комптона (упругом рассеянии фотона на свободном электроне):

.

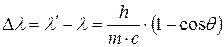Здесь – длина волны падающего (первичного) фотона, 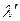– длина волны рассеянного фотона, 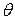– угол рассеяния, m – масса электрона (или протона, если рассеяние происходит на протоне).

· Комптоновская длина волны:

.

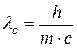Строение атома

· Постулат стационарных состояний (первый постулат Бора). Электрон в атоме может находиться только на стационарной орбите; при этом он не излучает и не поглощает энергии. Условие стационарных орбит:

; .

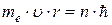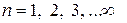Здесь 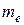– масса электрона; r – радиус орбиты; 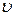– скорость электрона на орбите; п – главное квантовое число (номер орбиты); ħ – редуцированная постоянная Планка.

· Момент импульса электрона на стационарных орбитах

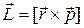, или .

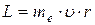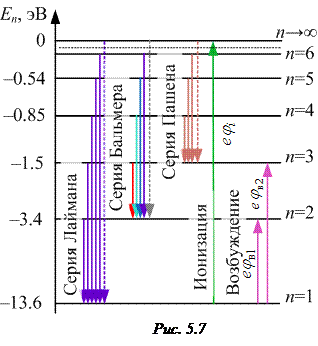Здесь 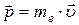– импульс электрона.

· Полная энергия электрона, находящегося на n-ой орбите водородоподобного иона (см. схему энергетических уровней на рис. 5.7):

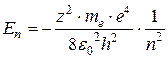, или .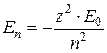

Здесь z – зарядовое число ядра водородоподобного иона; 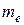– масса электрона; e – элементарный заряд, h – постоянная Планка; п – номер орбиты; ε₀ – электрическая постоянная; 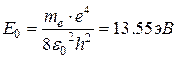– модуль энергии основного состояния атома водорода.

· Правило частот (второй постулат Бора). Энергия излучается или поглощается атомом только при переходе электрона между стационарными орбитами; при этом энергия 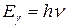излучённого или поглощённого кванта равна разности энергий стационарных состояний, между которыми произошёл переход:

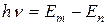, или .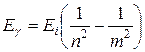

Здесь n и m – номера орбит (m>n), 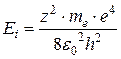– энергия ионизации водородоподобного иона. Для водорода (z=1) она равна .

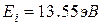· Сериальная формула, определяющая длину волны λ или частоту 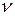света, излучаемого или поглощаемого водородоподобным ионом при переходе из одного стационарного состояния в другое:

; .

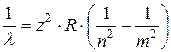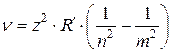Здесь n и m – номера орбит, между которыми произошёл переход: m=n+1; n+2; n+3…∞ (при n=1 получается серия Лаймана; n=2 – серия Бальмера; n=3 – серия Пашена; n=4 – серия Брэккета и т.д.; см. рис. 5.7); z – зарядовое число ядра; 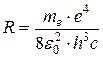(или 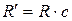) – постоянная Ридберга, c – скорость света.

· Энергия ионизации–энергия,которую необходимо затратить для того, чтобы удалить электрон из атома (перевести в состояние с квантовым числом n→∞); она равна разности энергий ионизированного состояния 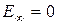и начального :

.

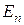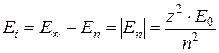Энергия ионизации атома водорода из основного состояния, то есть состояния с n=1, равна 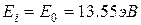(рис. 5.7).

· Потенциал ионизации атома водорода или водородоподобного иона

.

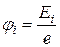Здесь 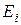– энергия ионизации, e – элементарный заряд. Потенциал ионизации из основного состояния атома водорода:

.

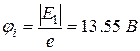· Потенциал возбуждения–потенциал, соответствующий энергии возбуждения атома, то есть энергии, необходимой для перехода атома из основного состояния (n=1) в возбуждённое (n=2 – первое возбуждённое состояние и первый потенциал возбуждения 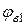; n=3 – второе возбуждённое состояние и второй потенциал возбуждения 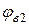и т.д., см. рис. 5.7):

, .

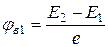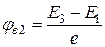Волновые свойства частиц.

· Длина волны де Бройля.

.

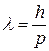Частице, имеющей импульс р и кинетическую энергию 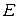, движущуюся вдоль оси OX, сопоставляется волна 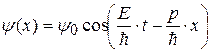. Здесь 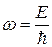– круговая частота; 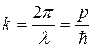– волновое число; h – постоянная Планка; 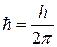. При скорости частицы υ<<c (с – скорость света в вакууме) длина волны де Бройля 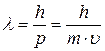, или .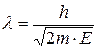

· Соотношения неопределённостей Гейзенберга

- для координаты и импульса частицы. Произведение неопределённостей 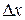координаты и соответствующей проекции импульса 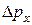частицы не меньше :

; ; .

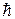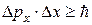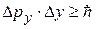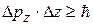- для энергии и времени. Произведение неопределенности 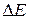энергии частицы и неопределённости 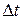момента времени:

.

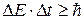Здесь h – постоянная Планка, 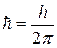– редуцированная постоянная Планка.

· Волновая функция (Ψ-функция) и её статистический смысл:волновая функция 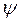описывает состояние микрообъекта в квантовой механике: вероятность dp обнаружить частицу в объёме dV вблизи заданной точки с координатами x, y, z равна 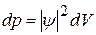. Или: квадрат модуля волновой функции есть плотность вероятности обнаружения частицы в данной точке:

.

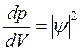· Стационарное уравнение Шрёдингера:

.

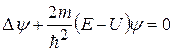Здесь Е – полная энергия частицы; U=U(x,y,z) – потенциальная энергия частицы; 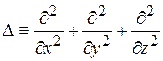– оператор Лапласа.

· Условие нормировки волновой функции:

.

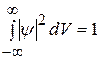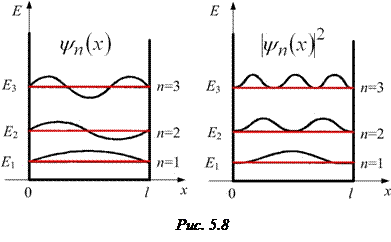· Решение уравнения Шрёдингера для частицы в одномерном потенциальном ящике с бесконечно высокими стенками (рис. 5.8):

,

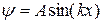где 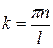; 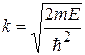– модуль волнового вектора; 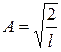– амплитуда волновой функции.

· Энергия частицы в одномерном потенциальном ящике с бесконечно высокими стенками (рис. 5.8):

,

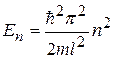где n – квантовое число, принимающее значения: n=1, 2, 3, …∞;

· Уравнение Шрёдингера для атома водорода (или водородоподобного иона):

.

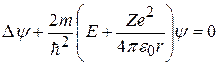Здесь 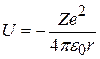– потенциальная энергия взаимодействия электрона с ядром.

· Квантовые числа – целочисленные параметры, от которых зависят волновая функция и энергия частицы. Состояние электрона в атоме описывается четырьмя квантовыми числами:

– главным n (n=1, 2, … ∞),

– орбитальным l (l=0, 1, 2, … n–1),

– магнитным m_l (m_l=0, ±1, ±2, … ±l),

– спиновым m_s ( ).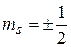

· Спиновый (собственный) момент импульса (механический момент) электрона в атоме ( 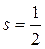– спин электрона):

.

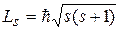· Проекция механического спинового момента электрона в атоме водорода на выделенное направление ( 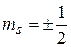– спиновое магнитное квантовое число):

.

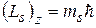· Орбитальный момент импульса (механический момент) электрона в атоме ( l – орбитальное квантовое число, принимающее значения: l=0, 1, 2 … n–1):

.

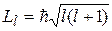· Проекция механического орбитального момента электрона в атоме на выделенное направление (m_l – магнитное квантовое число, принимающее значения: m_l=0, ±1, ±2, … ±l):

.

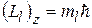· Полный момент импульса (механический момент) электрона в атоме (J – квантовое число полного момента: J=|l–s|, |l–s|+1, …l+s):

.

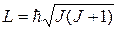Задачи к разделу 5

321. На мыльную пленку (n=1,3), находящуюся в воздухе, падает нормально пучок лучей белого света. При какой наименьшей толщине d пленки отраженный свет с длиной волны λ=0,55 мкм окажется максимально усиленным в результате интерференции?

322. На тонкий стеклянный клин (n=1,55) падает нормально монохроматический свет. Двугранный угол между поверхностями клина составляет 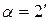. Определить длину световой волны, если расстояние между смежными интерференционными максимумами в отраженном свете b=0,3 мм.

323. Поверхности стеклянного клина (n=1,5) образуют между собой угол 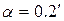. На клин нормально к его поверхности падает пучок лучей монохроматического света с длиной волны λ=0,55 мкм. Определить ширину интерференционной полосы.

324. На мыльную пленку (n=1,33) падает под углом 45⁰ параллельный пучок белого света. Определить минимальную толщину пленки, если в отраженном свете она кажется зеленой (длина волны 500 нм).

325. На тонкую пленку (показатель преломления 1.33) падает параллельный пучок белого света. Угол падения 52⁰. При какой минимальной толщине пленки зеркально отраженный свет будет наиболее сильно окрашен в желтый цвет (длина волны 600 нм)?

326. Найти минимальную толщину пленки с показателем преломления 1.33, при которой свет с длиной волны 640 нм испытывает максимальное отражение, а свет с длиной волны 400 нм не отражается совсем. Угол падения света равен 30⁰.

327. Установка для получения колец Ньютона освещается монохроматическим светом, падающим по нормали к поверхности пластинки. После того как пространство между линзой и пластинкой заполнили жидкостью, радиусы колец в отраженном свете уменьшились в 1.25 раза. Найти показатель преломления жидкости.

328. Определить радиус 4-ого темного кольца Ньютона, если между линзой с радиусом R=5 м и плоской поверхностью, к которой она прижата, находится вода (n=1,33). Длина волны света λ=5.89^.10^{-7 м.}

329. Определить радиус кривизны плосковыпуклой линзы, которая вместе с пластинкой позволяет наблюдать кольца Ньютона при освещении желтой линией натрия (длина волны 589 нм), причем в отраженном свете расстояние между первым и вторым светлыми кольцами равно 0.5 мм.

330. Расстояние между вторым и первым темными кольцами Ньютона в отраженном свете равно 1 мм. Определить расстояние между десятым и девятым кольцами.

331. Свет от монохроматического источника с λ=5^.10^{-7 м падает нормально на диафрагму с круглым отверстием диаметром 6 мм. На расстоянии 3 м от диафрагмы находится экран. Темным или светлым будет центр дифракционной картины на экране?}

332. Монохроматический свет с длиной волны 540 нм падает параллельным пучком на круглое отверстие нормально к плоскости отверстия. На каком расстоянии от отверстия должна находиться точка наблюдения, чтобы в отверстии помещалась одна зона Френеля? Диаметр отверстия 1 см.

333. Дифракционная картина наблюдается на расстоянии l от точечного источника монохроматического света с длиной волны 640 нм. На расстоянии а=0.5l от источника помещена круглая непрозрачная преграда диаметром 1 см. Найти расстояние l, если преграда закрывает только центральную зону Френеля.

334. На диафрагму с круглым отверстием радиусом r=1 мм падает нормально параллельный пучок света с длиной волны 0,5 мкм. На пути лучей, прошедших через отверстие, помещают экран. Определить максимальное расстояние b_max от центра отверстия до экрана, при котором в центре дифракционной картины еще будет наблюдаться темное пятно.

335. Радиус четвертой зоны Френеля для плоского волнового фронта равен 3 мм. Определить радиус шестой зоны Френеля.

336. На щель шириной а=6l падает нормально параллельный пучок монохроматического света. Под каким углом будет наблюдаться третий дифракционный минимум?

337. Дифракционная решетка шириной 12 мм содержит 4800 штрихов. Определить: а) число максимумов, наблюдаемых в спектре дифракционной решетки для λ=5.6^.10^{-7 м, б) угол, соответствующий последнему максимуму.}

338. Сколько штрихов на 1 мм должна иметь дифракционная решетка, чтобы углу 90⁰ соответствовал максимум пятого порядка для света с длиной волны 5^.10^{-7 м?}

339. Постоянная дифракционной решетки в 6.6 раза больше длины световой волны. На поверхность дифракционной решетки нормально к поверхности падает монохроматический свет. Найти общее число К дифракционных максимумов, которые теоретически возможно наблюдать в данном случае.

340. На щель шириной, а=0,05 мм падает нормально монохроматический свет (λ=0,6 мкм). Определить угол между первоначальным направлением пучка света и направлением на четвертую темную дифракционную полоску.

341. Один поляроид пропускает 30% света, если на него падает естественный свет. После прохождения света через 2 поляроида интенсивность падает до 13.5%. Найти угол между осями поляроидов.

342. Луч света последовательно проходит через 2 николя, плоскости пропускания которых образуют угол 45⁰. Принимая, что коэффициент поглощения каждого николя равен 0.2, найти, во сколько раз луч, выходящий из второго николя, ослаблен по сравнению с лучом, падающим на первый николь. Свет естественный.

343. Угол φ между плоскостями пропускания поляроидов равен 60⁰. Естественный свет, проходя через такую систему, ослабляется в 12.5 раз. Пренебрегая потерей света при отражении, определить коэффициент поглощения света в поляроидах.

344. Пучок естественного света падает на систему из 4-х николей, плоскость пропускания каждого из которых повернута на угол 30⁰ относительно плоскости пропускания каждого предыдущего николя. Какая часть энергии падающего пучка проходит через такую систему?

345. Угол между главными плоскостями поляризатора и анализатора равен 45⁰. Во сколько раз уменьшится интенсивность света, выходящего из анализатора, если угол увеличить до 60⁰?

346. Чему равен угол между главными плоскостями поляризатора и анализатора, если интенсивность естественного света, прошедшего через поляризатор и анализатор, уменьшилась в 4 раза? Поглощением пренебречь.

347. Чему равен угол между главными плоскостями поляризатора и анализатора, если интенсивность естественного света, прошедшего через поляризатор и анализатор, уменьшится в 6 раз? Поглощение света в поляризаторе и анализаторе по 15%.

348. Угол между плоскостями поляризации двух поляроидов 35⁰. Как изменится интенсивность прошедшего через них света, если этот угол увеличить вдвое?

349. Естественный свет проходит через поляризатор и анализатор, поставленные так, что угол между их главными плоскостями равен φ. Как поляризатор, так и анализатор поглощают и отражают по 40% падающего на них света. Оказалось, что интенсивность луча, вышедшего из анализатора, равна 9% интенсивности естественного света, падающего на поляризатор. Найти угол φ.

350. При падении на некоторый поляризатор естественного света проходит 40% светового потока, а при падении плоскополяризованного света – 60%. Найти угол между плоскостью колебаний падающего света и главной плоскостью поляризатора.

351. Вследствие изменения температуры абсолютно черного тела максимум спектральной плотности энергетической светимости сместился с 2400 нм на 800 нм. Как и во сколько раз изменились энергетическая светимость тела и максимальное значение спектральной плотности энергетической светимости?

352. Определить количество теплоты, теряемое поверхностью расплавленной платины площадью 50 см² за 1 минуту, если поглощательная способность платины равна 0.8. Температура плавления платины 1772⁰С.

353. Определите энергию, излучаемую через смотровое окошко печи за время t=5 с. Площадь окошка равна S=5,5 см², максимум в спектре излучения приходится на длину волны λ_m=1,6 мкм.

354. Модель абсолютно чёрного тела – полость с малым круглым отверстием диаметром d=1,5 см. Нагрев производится электрической спиралью, потребляющей ток I=35 мА при напряжении U=220 В, причём некоторая доля мощности рассеивается стенками полости. Равновесная температура излучения, исходящего из отверстия, равна Т=870 К. Определить рассеиваемую мощность ΔP.

355. Какое количество энергии излучает в течении суток каменное оштукатуренное здание с общей площадью поверхности 1000 м², если коэффициент поглощения (поглощательная способность) при этом равен 0,8 и температура излучающей поверхности 0^°С?

356. Стальная болванка, температура которой 727^°С, излучает за 1 с 4 Дж энергии с поверхности 1 см². Определить коэффициент поглощения (поглощательную способность) болванки при данной температуре, считая, что он одинаков для всех длин волн.

357. Поверхность тела нагрета до температуры 1000 К. Затем одна половина этой поверхности нагревается на 100 К, а другая охлаждается на 100 К. Во сколько раз изменится энергетическая светимость поверхности этого тела?

358. Температура абсолютно черного тела изменилась при нагревании от 1000 К до 3000 К. 1) Во сколько раз увеличилась при этом его энергетическая светимость? 2) Насколько изменилась при этом длина волны, на которую приходится максимум спектральной плотности энергетической светимости? 3) Во сколько раз увеличилась его максимальная спектральная плотность энергетической светимости?

359. Поток излучения абсолютно черного тела 10⁴ Вт, максимум спектральной плотности энергетической светимости приходится на длину волны 10^{-6 м. Определить площадь излучающей поверхности.}

360. Абсолютно черное тело находится при температуре 3000 К. В результате остывания этого тела длина волны, на которую приходится максимум спектральной плотности энергетической светимости, изменилась на 12 мкм. До какой температуры охладилось тело?

361. Поток монохроматического излучения (λ=500 нм) падает нормально на плоскую зеркальную поверхность и давит на неё с силой 10^-8 Н. Определить число фотонов, ежесекундно падающих на эту поверхность.

362. Параллельный пучок монохроматических лучей (λ=662 нм) падает на зачерненную поверхность и производит на неё давление 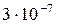Н/м². Определить концентрацию фотонов в световом пучке.

363. На расстоянии 5 м от точечного монохроматического изотропного источника света с длиной волны 5^.10^{-7 м} перпендикулярно падающим лучам расположена площадка площадью 10^{-6 м2}. Определить число фотонов, ежесекундно падающих на площадку. Мощность излучения 100 Вт.

364. Определить давление солнечных лучей, нормально падающих на зеркальную поверхность. Интенсивность солнечного излучения принять равной 1,37 кВт/м².

365. Определить плотность потока энергии излучения I, падающего на зеркальную поверхность, если световое давление при перпендикулярном падении лучей равно р=10 мкПа.

366. Мощность, излучаемая электрической лампой, равна 600 Вт. На расстоянии r=1 м от лампы перпендикулярно падающим лучам расположено круглое плоское зеркальце диаметром d=2 см. Принимая, что излучение лампы одинаково во всех направлениях и что зеркальце полностью отражает падающий на него свет, определить силу светового давления на зеркальце.

367. На зеркальце с идеально отражающей поверхностью площадью S=1,5 см² падает нормально свет от электрической дуги. Определить импульс р, полученный зеркальцем, если интенсивность излучения, падающего на зеркальце, равна I=0,1 МВт/м². Продолжительность облучения Δt=1 c.

368. Плотность потока энергии в импульсе излучения лазера может достигать значения 1,3∙10²⁰ Вт/м². Определить давление такого излучения, нормально падающего на черную поверхность.

369. Свет с длиной волны λ=500 нм нормально падает на зеркальную поверхность и производит на неё давление р=4 мкПа. Определить число фотонов, ежесекундно падающих на 1 см²этой поверхности.

370. Импульс, переносимый плоским монохроматическим потоком за 5 с через площадку 10^{-3 м2}, перпендикулярную световым лучам, равен 10^{-11 кг.}м/с. Определить интенсивность света и давление, оказываемое им на площадку. Коэффициент отражения 0.5.

371. На платиновую пластинку (А_вых=5.3 эВ) падают ультрафиолетовые лучи. Для прекращения фотоэффекта нужно приложить задерживающую разность потенциалов 3,7 В. Если платиновую пластинку заменить пластинкой из другого металла, то задерживающую разность потенциалов нужно увеличить до 6 В. Определить работу выхода электронов с поверхности этой пластинки.

372. При поочередном освещении поверхности некоторого металла светом с длинами волн λ₁=0,35 мкм и λ₂=0,54 мкм обнаружили, что соответствующие максимальные скорости фотоэлектронов отличаются друг от друга в n=2 раза. Найти работу выхода с поверхности этого металла.

373. Красная граница фотоэффекта для рубидия 570 нм. Какую обратную разность потенциалов нужно приложить к фотоэлементу, чтобы задержать электроны, испускаемые рубидием под действием ультрафиолетовых лучей длиной волны 100 нм?

374. При падении излучения с длиной волны λ на пластинку из металла с красной границей фотоэффекта λ₁=0,35 мкм задерживающее напряжение для фотоэлектронов равно U₁=1,4 В, а при падении на пластинку с красной границей λ₂=0,45 мкм оно равно U₂. Определить U₂.

375. Определить импульс электрона отдачи при