Уравнения процессов с идеальным газом, первое начало термодинамики для них, термодинамические величины и их изменения при этих процессах

Процесс	T=const Изотерма	V=const Изохора	p=const Изобара	S=const Адиабата
Уравнение процесса
Первое начало термодинамики
Работа газа A
Изменение внутренней энергии ΔU
Количество теплоты Q
Изменение энтропии ΔS

· Удельная теплота парообразования:

,

где m масса вещества; Q – теплота, необходимая для его испарения.

· Удельная теплота плавления:

,

где m – масса вещества; Q – теплота, необходимая для его плавления.

Задачи к разделу 2

81. В сосуд диаметром D заливается вода со скоростью Q=0,5 л/с. Пренебрегая вязкостью воды, определить диаметр d отверстия в сосуде, при котором вода поддерживалась бы на постоянном уровне h=20 см. Считать d<<D.

82. Вода течёт в горизонтально расположенной трубе переменного сечения. Скорость воды в широкой части трубы 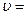20 см/с. Определить скорость в узкой части трубы, диаметр которой в 1,5 раза меньше диаметра широкой части.

83. В широкой части горизонтально расположенной трубы нефть течёт со скоростью 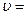2 м/с. Определить скорость нефти в узкой части трубы, если разность давлений в широкой и узкой частях её равна Δp=6,65 кПа. Плотность нефти ρ=900 кг/м³.

84. Струя воды диаметром 2 см, движущаяся со скоростью 10 м/с, ударяется о неподвижную плоскую поверхность, поставленную перпендикулярно струе. Найти силу давления струи на поверхность, считая, что после удара о поверхность скорость частиц воды равна нулю.

85. Струя воды с площадью поперечного сечения S₁=4 см² вытекает в горизонтальном направлении из брандспойта, расположенного на высоте h=2 м над поверхностью Земли, и падает на эту поверхность на расстоянии l=8 м. Пренебрегая сопротивлением воздуха, найти избыточное давление воды в рукаве, если площадь поперечного сечения рукава S₂=50 см².

86. Из брандспойта бьёт струя воды, дающая 60 л за 1 мин. Площадь отверстия в брандспойте S₁=1,5 см². Насколько больше атмосферного давления давление внутри шланга в том месте, которое на 3 м ниже конца брандспойта? Площадь канала шланга S₂=10 см².

87. В сосуд льётся вода, причем за секунду наливается объём воды 0,2 л. Каким должен быть диаметр отверстия в дне сосуда, чтобы вода в нем держалась на постоянном уровне h=8,3 см?

88. Какое давление создает компрессор в краскопульте, если струя жидкой краски вытекает из него со скоростью 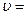25 м/с? Плотность краски 800 кг/м³.

89. Какую силу необходимо приложить к поршню горизонтально расположенной спринцовки, чтобы вытекающая из неё струя воды имела скорость 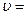10 м/с? Радиус поршня r=2 см. Трением пренебречь.

90. Определить скорость течения воды в широкой части горизонтально расположенной трубы переменного сечения, если радиус узкой части в 3 раза меньше радиуса широкой части, а разность давлений в широкой и узкой частях трубы 10 кПа.

91. Вода течёт по круглой гладкой трубе диаметром d=5 см со средней по сечению скоростью 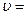10 см/с. Определить число Рейнольдса для потока жидкости в трубе и указать характер течения жидкости.

92. По трубе течет машинное масло. Максимальная скорость, при которой движение масла в этой трубе остается ещё ламинарным, равна 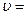3,2 см/с. При какой скорости движение глицерина в той же трубе переходит из ламинарного в турбулентное?

93. Латунный шарик диаметром d=0,5 мм падает в глицерине. Определить: а) скорость установившегося движения шарика; б) является ли при этом значении скорости обтекание шарика ламинарным? Критическое значение числа Рейнольдса Re_кр=0,5.

94. Смесь свинцовых дробинок диаметром d₁=4 мм и d₂=2 мм одновременно опускают в широкий сосуд глубиной h=1,5 м с глицерином. Определить, насколько больше времени потребуется дробинкам меньшего размера, чтобы достичь дна сосуда.

95. В широком сосуде, наполненном глицерином, падает свинцовый шарик. Считая, что при числе Рейнольдса Re<0,5 выполняется закон Стокса, определить предельный размер шарика.

96. Какой наибольшей скорости может достичь дождевая капля диаметром d=0,3 мм?

97. При движении шарика радиусом r=3 мм в глицерине ламинарное обтекание наблюдается при скорости шарика, не превышающей 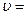23 см/с. При какой минимальной скорости шарика радиусом r=5,5 мм в воде обтекание примет турбулентный характер?

98. Площадь соприкосновения слоёв текущей жидкости S=10 см², коэффициент динамической вязкости жидкости 10^-3 Па∙с, а возникающая сила трения между слоями F=0,1 мН. Определить градиент скорости.

99. Вычислить максимальное значение скорости потока воды в трубе диаметром d₁=2 см, при котором течение будет оставаться ламинарным. Критическое значение числа Рейнольдса для трубы приблизительно равно Re=3000. Каково соответствующее значение скорости для трубки диаметром d₂=0,1 см?

100. Медный шарик диаметром d=1 см падает с постоянной скоростью в касторовом масле. Является ли движение масла, вызванное падением в нем шарика, ламинарным? Критическое значение числа Рейнольдса Re=0,5.

101. Свинцовая проволока подвешена в вертикальном положении за верхний конец. Какую наибольшую длину может иметь проволока, не обрываясь под действием силы тяжести?

102. К вертикальной проволоке длиной l=5 м и площадью поперечного сечения S=2 мм² подвешен груз массой 5,1 кг. В результате проволока удлинилась на 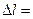0,6 мм. Найти модуль Юнга материала проволоки.

103. Какую работу нужно совершить, чтобы растянуть на 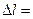1 мм стальной стержень длиной l=1 м и площадью поперечного сечения S=1 см²?

104. Резиновый шнур растянут так, что его длина увеличилась в 2 раза. Каков диаметр растянутого шнура, если до растяжения он был d=1см, а коэффициент Пуассона для резины µ=0,5?

105. Определить относительное изменение объёма стальной проволоки диаметром d=2 мм при растяжении её силой F=1 кН. Коэффициент Пуассона равен µ=0,3.

106. При какой длине подвешенная вертикально стальная проволока начинает рваться под действием собственного веса?

107. Определить относительное удлинение медного стержня, если при его растяжении затрачена работа А=0,12 Дж. Длина стержня l=2 м, площадь поперечного сечения S=1 мм².

108. Определить силу, с которой гимнаст массой m=60 кг действует на упругую сетку при прыжке с высоты h=8 м, если под действием веса гимнаста сетка прогибается на 16 см.

109. К проволоке из углеродистой стали длиной l=1,5 м и диаметром d=2,1 мм подвешен груз массой 110 кг. Принимая для стали модуль Юнга Е=216 ГПа и предел пропорциональности 330 МПа, определить: а) какую долю первоначальной длины составляет удлинение проволоки при этом грузе; б) превышает приложенное напряжение или нет предел пропорциональности.

110. Определить относительное удлинение алюминиевого стержня, если при его растяжении затрачена работа А=6,9 Дж. Длина стержня l=1 м, площадь поперечного сечения S=1 мм², модуль Юнга для алюминия Е=69 ГПа.

111. В баллоне объёмом V=0,25 м³ находится смесь кислорода и гелия. Число молекул кислорода N₁=6,6∙10²¹, а число молекул гелия N₂=0,9∙10²¹. Температура смеси Т=620 К. Определить давление смеси p.

112. В баллоне объёмом V находится смесь кислорода и гелия. Число молекул кислорода N₁, а число молекул гелия N₂=1,2∙10²¹. Температура смеси Т=530 К, давление смеси p=250 Па, среднее значение молярной массы смеси 22 кг/кмоль. Определить объём V.

113. В баллоне объёмом V=0,15 м³ находится смесь кислорода и гелия. Число молекул кислорода N₁=5,1∙10²¹, а число молекул гелия N₂. Давление смеси p=460 Па, среднее значение молярной массы смеси 13 кг/кмоль. Определить температуру смеси.

114. В сосуде объёмом V=10 л находится смесь двух газов: газ с молярной массой 32 г/моль в количестве m₁=23 г и газ с молярной массой 4 г/моль в количестве m₂=15 г. Давление в сосуде равно p=1,2 МПа. Определить температуру Т в сосуде.

115. В сосуде объёмом V находится смесь двух газов: газ с молярной массой 2 г/моль в количестве m₁=1,1 г и газ с молярной массой 4 г/моль в количестве m₂=2,9 г. Давление в сосуде равно p=0,53 МПа. Температура смеси t=75⁰C. Определить объём V сосуда.

116. В сосуде объёмом V=1,5 л находится смесь двух газов: газ с молярной массой 28 г/моль в количестве m₁=0,15 г и газ с молярной массой 2 г/моль в количестве m₂=0,14 г. Температура смеси t= –15⁰C. Определить давление p смеси.

117. В цилиндре под невесомым поршнем находился воздух в объёме V₁=2,4 л при температуре t₁=26⁰C и атмосферном давлении p₁=730 мм. рт. ст. После погружения цилиндра в воду с температурой t₂=12⁰C на глубину h объём воздуха уменьшился до V₂=1,9 л. Определить глубину h.

118. В цилиндре под невесомым поршнем находился воздух в объёме V₁=6,1 л при температуре t₁=57⁰C и атмосферном давлении p₁=750 мм. рт. ст. После погружения цилиндра в воду с температурой t₂ на глубину h=5 м объём воздуха уменьшился до V₂=3,5 л. Определить температуру t₂.

119. В цилиндре под невесомым поршнем находился воздух в объёме V₁ при температуре t₁=77⁰C и атмосферном давлении p₁=570 мм. рт. ст. После погружения цилиндра в воду с температурой t₂=15⁰C на глубину h=8,5 м объём воздуха уменьшился до V₂=1,7 л. Определить объем V₁.

120. Два сосуда соединены трубкой с краном. В одном находится кислород массой m₁=1,8 кг под давлением p₁=250 кПа, а в другом – углекислый газ массой m₂=4,3 кг под давлением p₂=720 кПа. После открывания крана и перемешивания газов давление смеси стало равным p. Температура газов до и после перемешивания одинакова. Определить давление p.

121. Два сосуда соединены трубкой с краном. В одном находится кислород массой m₁=4,9 кг под давлением p₁=210 кПа, а в другом – углекислый газ массой m₂ под давлением p₂=540 кПа. После открывания крана и перемешивания газов давление смеси стало равным p=430 кПа. Температура газов до и после перемешивания одинакова. Определить массу m₂.

122. Из баллона объёмом V=60 л, содержащего сжатый воздух при давлении p₁=7,5 МПа и температуре t₁, постепенно выпускают массу воздуха m=2,6 кг. После закрывания крана давление воздуха в баллоне p₂=3,5 МПа, температура t₂= –25⁰C. Определить температуру t₁. Средняя молярная масса воздуха µ=0.029 кг/моль.

123. Из баллона объёмом V=25 л, содержащего сжатый воздух при давлении p₁=3,9 МПа и температуре t₁=35⁰C, постепенно выпускают массу воздуха m=0,48 кг. После закрывания крана давление воздуха в баллоне p₂, температура t₂= –15⁰C. Определить давление p₂. Средняя молярная масса воздуха µ=0.029 кг/моль.

124. Из баллона объёмом V=50 л, содержащего азот при температуре t₁=27⁰C, выпускается часть газа столь быстро, что теплообмен газа в баллоне с атмосферой за время выпускания не успевает произойти. Сразу после закрывания крана температура газа в баллоне t₂= 0⁰C, давление p₂=2,88 МПа. Определить массу выпущенного азота.

125. Из баллона объёмом V=60 л, содержащего азот при температуре t₁, выпускается часть газа столь быстро, что теплообмен газа в баллоне с атмосферой за время выпускания не успевает произойти. Сразу после закрывания крана температура газа в баллоне t₂= –15⁰C, давление p₂=3,7 МПа. Масса выпущенного азота m=1,12 кг. Определить температуру t₁.

126. Цикл, совершаемый одним киломолем идеального двухатомного газа, состоит из двух изохор и двух изобар. Совершаемая газом за цикл работа равна А=32 кДж. Минимальные значения объёма и давления равны p₁=170 кПа, V₁=0,25 м³, максимальные – V₂=0,85 м³ и p₂. Определить p₂, количество полученной от нагревателя теплоты Q₁ и количество отданной холодильнику теплоты Q₂.

127. Цикл, совершаемый одним киломолем идеального двухатомного газа, состоит из двух изохор и двух изобар. Минимальные значения объёма и давления равны V₁=0,075 м³, p₁=330 кПа, максимальные – V₂=0,135 м³ , p₂=460 кПа. Определить совершаемую газом за цикл работу А, количество полученной от нагревателя теплоты Q₁ и количество отданной холодильнику теплоты Q₂.

128. Некоторая масса газа с двухатомными молекулами при давлении p₁=140 кПа имела объём V₁=0,95 м³, а при давлении p₂=330 кПа – объём V₂=0,44 м³. Переход от первого состояния ко второму был сделан в два этапа: сначала по изобаре, а затем по адиабате. Определить приращение внутренней энергии газа ∆U при таком переходе.

129. Некоторая масса газа с двухатомными молекулами при давлении p₁=1300 кПа имела объём V₁=1,35 м³, а при давлении p₂=850 кПа – объём V₂=1,47 м³. Определить работу газа А, если переход от первого состояния ко второму был сделан в два этапа: сначала по изобаре, а затем по адиабате.

130. Некоторая масса газа с двухатомными молекулами при давлении p₁=710 кПа имела объём V₁=0,94 м³, а при давлении p₂=320 кПа – объём V₂=0,82 м³. Переход от первого состояния ко второму был сделан в два этапа: сначала по изобаре, а затем по адиабате. Определить количество поглощённой теплоты Q.

131. Двухатомный газ при давлении p₁=270 кПа имел объём V₁=0,14 м³, при давлении p₂=320 кПа – объём V₂=0,11 м³. Переход от первого состояния ко второму был сделан в два этапа: сначала по изотерме, а затем по изохоре. Определить количество поглощённой теплоты Q.

132. Двухатомный газ при давлении p₁=440 кПа имел объём V₁=0,83 м³, при давлении p₂=120 кПа – объём V₂=0,39 м³. Переход от первого состояния ко второму был сделан в два этапа: сначала по изотерме, а затем по изохоре. Определить приращение внутренней энергии ∆U.

133. Двухатомный газ при давлении p₁=1200 кПа имел объём V₁=0,18 м³, при давлении p₂=850 кПа – объём V₂=0,42 м³. Переход от первого состояния ко второму был сделан в два этапа: сначала по изотерме, а затем по изохоре. Определить работу газа А.

134. Водород находился при давлении p₁=1750 кПа в объёме V₁=0,33 м³, а при изменении объёма до V₂=0,68 м³ давление его стало равным p₂=250 кПа. Переход от первого состояния ко второму был сделан в два этапа: сначала по изохоре, а затем по адиабате. Определить количество поглощённой теплоты Q.

135. Водород находился при давлении p₁=320 кПа в объёме V₁=1,75 м³, а при изменении объёма до V₂=0,95 м³ давление его стало равным p₂=450 кПа. Переход от первого состояния ко второму был сделан в два этапа: сначала по изохоре, а затем по адиабате. Определить работу газа А, совершённую при таком переходе.

136. Водород находился при давлении p₁=260 кПа в объёме V₁=0,47 м³, а при изменении объёма до V₂=0,24 м³ давление его стало равным p₂=150 кПа. Переход от первого состояния ко второму был сделан в два этапа: сначала по изохоре, а затем по адиабате. Определить приращение внутренней энергии ∆U.

137. Кислород массой m=2 кг занимает объём V₁=1 м³ и находится под давлением p₁=0,2 МПа. Газ был нагрет сначала при постоянном давлении до объёма V₂=3 м³, а затем при постоянном объёме до давления p₂=0,5 МПа. Найти изменение внутренней энергии газа ∆U, совершенную работу А и теплоту Q, переданную газу. Построить график процесса.

138. В цилиндре под поршнем находится водород массой m=0,02 кг при температуре T₁=300 К. Водород сначала расширился адиабатически, увеличив свой объём в пять раз, а затем был сжат изотермически, причём объём газа уменьшился в пять раз. Найти температуру в конце адиабатического расширения и полную работу, совершенную газом. Изобразить процесс графически.

139. При адиабатическом сжатии 20 г гелия давление газа увеличилось в 10 раз. Определить конечную температуру газа T₂ и работу сжатия А. Начальная температура гелия равна T₁=300 К.

140. Один килограмм кислорода сжимается адиабатически, вследствие чего температура газа возрастает от 20°С до 500°С. Вычислить: а) приращение внутренней энергии газа ∆U; б) работу, затраченную на сжатие газа А_сж.; в) во сколько раз уменьшится объём газа?

141. В цикле Карно газ получил от нагревателя количество теплоты, равное 500 Дж, и совершил работу 100 Дж. Температура нагревателя 400 К. Определить температуру холодильника.

142. Газ, совершающий цикл Карно, получает теплоту 84 кДж. Какую работу совершает газ, если температура нагревателя в три раза выше температуры охладителя?

143. Газ, совершающий цикл Карно, отдал охладителю теплоту 14 кДж. Определить температуру нагревателя, если при температуре охладителя 280 К работа цикла равна 6 кДж.

144. При прямом цикле Карно тепловая машина совершает работу 1000 Дж. Температура нагревателя 500 К, температура холодильника 300 К. Определить количество теплоты, получаемое машиной от нагревателя.

145. Идеальный газ совершает цикл Карно при температурах нагревателя 400 К и холодильника 290 К. Во сколько раз увеличится коэффициент полезного действия цикла, если температура нагревателя возрастет до 600 К?

146. Идеальный газ совершает цикл Карно. Температура нагревателя в четыре раза больше температуры холодильника. Какую долю количества теплоты, полученного за один цикл от нагревателя, газ отдаст холодильнику?

147. Определить работу изотермического сжатия газа, совершающего цикл Карно, коэффициент полезного действия которого η=0,4, если работа изотермического расширения составляет 8 Дж.

148. Газ, совершающий цикл Карно, отдал холодильнику 67% теплоты, полученной от нагревателя. Определить температуру холодильника, если температура нагревателя 430 К.

149. Газ, совершающий цикл Карно, получил от нагревателя количество теплоты, равное 4,38 кДж, и совершил работу 2,4 кДж. Определить температуру нагревателя, если температура холодильника 273 К.

150. Идеальный газ совершает цикл Карно. Температура нагревателя равна 470 К, температура охладителя 280 К. При изотермическом расширении газ совершает работу 100 Дж. Определить термический КПД цикла, а также количество теплоты, которое отдает охладителю при изотермическом сжатии газ.

151. Кислород массой 5 кг увеличил свой объём в 5 раз, один раз – изотермически, другой – адиабатически. Каково будет изменение энтропии в двух этих случаях?

152. Кусок льда массой 200 г, взятый при температуре –10°С, был нагрет до 0°С и расплавлен, после чего образовавшаяся вода была нагрета до температуры 10°С. Определить изменение энтропии льда.

153. Смешивают 4 кг воды при 80°C и 6 кг воды при 20°C. Определить изменение энтропии при этом процессе.

154. Струя водяного пара при температуре 100°C, направленная на глыбу льда массой 4 кг при температуре –20°C, растопила её и нагрела получившуюся воду до 60 °C. Найти изменение энтропии этом процессе.

155. Один килограмм кислорода при давлении 0,5 МПа и температуре 127°C, изобарически расширяясь, увеличивает свой объём в 2 раза, а затем сжимается изотермически до давления 4 МПа. Определить суммарное изменение энтропии.

156. Определить изменение энтропии 14 г азота при изобарном нагревании его от 27 °C до 127 °C.

157. Как изменится энтропия 2 молей углекислого газа при изотермическом расширении, если объём газа увеличивается в четыре раза?

158. Найти изменение энтропии при кристаллизации 2 кг свинца при температуре 327°C и дальнейшем его охлаждении до 0°C. Удельная теплоёмкость свинца равна 130 Дж/(кг^.К); удельная теплота плавления – 25 кДж/кг.

159. Определить изменение энтропии, происходящее при смешивании 2 кг воды, находящейся при температуре 300 К, и 4 кг воды, находящейся при температуре 370°C.

160. Лёд массой 1 кг, находящийся при температуре 0°C, нагревают до температуры 57°C. Определить изменение энтропии.