Раздел 6. Статистическая физика. Физика твёрдого тела. Строение ядра

Молекулярно-кинетическая теория (МКТ). Статистический и термодинамический методы. Макроскопические параметры. Уравнение состояния. Основное уравнение МКТ для давления, для температуры. Молекулярно-кинетический смысл температуры. Число степеней свободы. Теорема о равнораспределении.

Понятие о классической статистике. Вероятность, среднее арифметическое, среднее квадратичное. Функция распределения вероятностей случайной величины. Распределение Максвелла. Характерные скорости молекул газа. Распределение Больцмана. Барометрическая формула.

Явления переноса. Эффективное сечение. Средняя длина свободного пробега, среднее число столкновений молекулы. Диффузия, вязкость, теплопроводность. Коэффициенты диффузии, вязкости, теплопроводности.

Твёрдое тело: упругие свойства, тепловое расширение, классическая теория теплоемкости твёрдых тел.

Квантовые статистики. Распределение Бозе-Эйнштейна и Ферми-Дирака. Электропроводность металлов. Электронный Ферми-газ в металле. Уровень Ферми. Энергия Ферми Элементы зонной теории кристаллов.

Полупроводники. Температурная зависимость сопротивления металлов и полупроводников. Контактные явления: p-n–переход; эффект Зеебека.

Состав и характеристики атомного ядра. Ядерные силы, дефект массы, энергия связи. Радиоактивный распад, виды распада, закон радиоактивного распада. Активность.

Контрольные работы и требования к их оформлению

Контрольные работы позволяют закрепить теоретический материал. Решение задач является проверкой степени усвоения студентами теоретического курса, а рецензии на работу помогают ему доработать и правильно усвоить различные разделы курса физики. Контрольные работы выполняются в период между сессиями и отдаются на кафедру физики для проверки не позднее, чем за 15 дней до начала сессии.

Перед выполнением контрольной работы необходимо внимательно ознакомиться с теоретическими и справочными материалами, а также примерами решения задач по данной теме.

Номер варианта контрольной работы выбирается студентом по последней цифре в зачетной книжке. Таблицы вариантов по каждой части курса физики представлены после приложений в конце учебного пособия.

Решенные задачи следует оформить так, как указано ниже.

При наличии значительных ошибок и неправильных решений работа возвращается студенту для исправлений. После исправления работа отправляется на кафедру физики на повторное рецензирование. Защита контрольных работ происходит в виде собеседования по решенным задачам на консультациях во время сессии.

1. Контрольная работа оформляется в отдельной тетради. Титульный лист оформляется следующим образом:

Контрольная работа по физике №…

“Название к.р.”

Студент ----------- группы ----------

......................................Шифр………..

Фамилия, Имя, Отчество

Вариант №…………………..

Проверил……………………………

Фамилия, Имя, Отчество преподавателя

“Зачтено”дата…………….роспись……….

2. Каждая задача оформляется с начала нового листа. Записывается полностью текст задачи так, как он приведен в методичке.

3. Все содержащиеся в задаче данные, которые могут быть представлены в виде математических соотношений, должны быть записаны в колонке под заголовком “Дано”.

4. Величины, выраженные через внесистемные единицы, должны быть выражены через единицы системы СИ. Численное значение всех величин должно быть представлено в нормализованном виде: (1÷10)^.10ⁿ.

5. Решению задачи должно предшествовать изображение физических явлений и процессов, происходящих в данной задаче. На рисунке, чертеже или блок-схеме должны быть указаны характерные параметры данной задачи, известные и искомые величины.

6. Задачу рекомендуется решить сначала в общем виде, то есть только в буквенных обозначениях, поясняя при написании формул буквенные обозначения. Решение задачи должно содержать краткие пояснения основных этапов. Значение фундаментальных физических констант должно быть приведено с указанием численного значения и размерности в системе СИ.

Контрольные работы, оформленные без соблюдения правил, а также работы, выполненные не по своему варианту, зачтены не будут.

Раздел 1. ФИЗИЧЕСКИЕ ОСНОВЫ МЕХАНИКИ

Кинематика

· Радиус-вектор 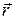материальной точки задаёт её положение в пространстве (рис. 1.1):

,

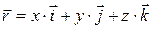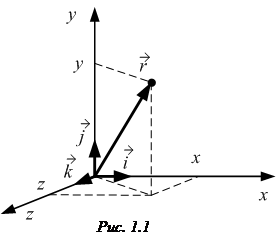где x, y и z – координаты точки; 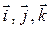– единичные векторы (орты), направленные вдоль осей OX, OY и OZ соответственно. Модуль вектора :

.

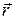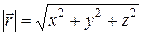· Кинематическое уравнение движения:

;

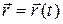или в координатной форме:

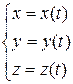
где t – время.

· Перемещение 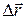материальной точки – вектор, соединяющий начальное (M₀)и конечное (M) её положение (рис.1.2). Перемещение равно

,

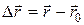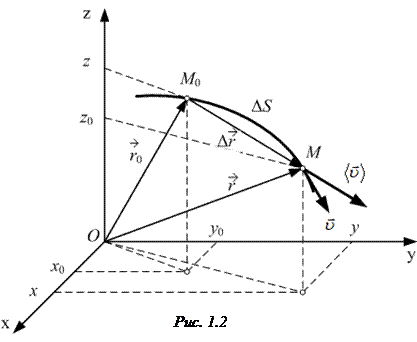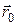где и 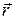– радиус-векторы начального и конечного положений точки соответственно.

· Путь 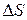– длина траектории (рис.1.2).

· Средняя скорость:

,

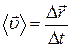где 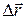– перемещение материальной точки за интервал времени .

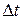· Средняя путевая скорость (средняя скорость вдоль траектории):

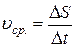
где 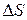– путь (длина траектории), пройденный точкой за интервал времени .

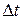· Мгновенная скорость:

;

,

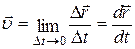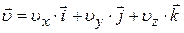где 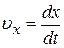, , 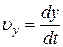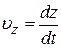– проекции скорости 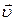на оси координат.

· Модуль скорости:

.

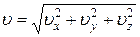· Закон сложения скоростей:

,

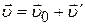где 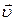– абсолютная, 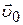– переносная, 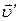– относительная скорости.

· Ускорение:

Среднее ускорение – изменение скорости за единицу времени:

,

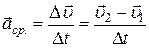где 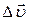– изменение скорости, произошедшее за промежуток времени .

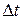Мгновенное ускорение – быстрота изменения скорости во времени; производная скорости по времени:

;

,

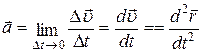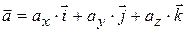где 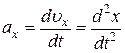, , 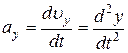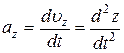– проекции ускорения 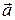на оси координат.

· Модуль ускорения: .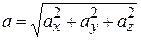

· При равномерном движени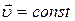и и .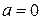

· Кинематическое уравнение равномерного движения материальной точки:

,

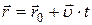или вдоль оси OX:

,

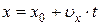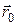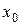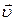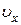где и – радиус-вектор и координата начального положения точки соответственно; и – скорость тела и её проекция на ось OX; t – время.

· При равнопеременном движении .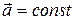

· Скорость точки при равнопеременном движении:

,

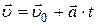или в проекции на ось OX:

.

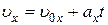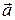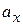где и – ускорение и его проекция на ось OX, 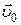и 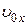– начальная скорость и её проекция на ось OX.

· Кинематическое уравнение равнопеременного движения:

,

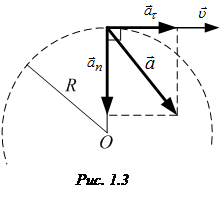
или вдоль оси OX:

.

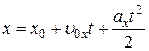· Ускорение при криволинейном движенииможно представить как сумму нормальной 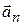и тангенциальной 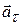составляющих (рис.1.3):

;

.

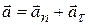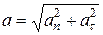· Нормальное ускорение

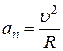
и направлено к центру кривизны траектории перпендикулярно ей. Здесь R – радиус кривизны траектории в данной точке. Нормальное ускорение показывает быстроту изменения скорости по направлению.

· Тангенциальное (касательное) ускорение

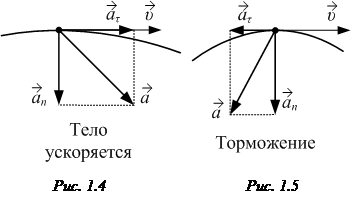
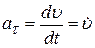
и направлено по касательной к траектории. Оно показывает быстроту изменения скорости по величине. Касательное ускорение направлено так же, как и скорость, если она возрастает по модулю (тело ускоряется, рис. 1.4); в случае торможения тела касательное ускорение направлено противоположно скорости (рис. 1.5).

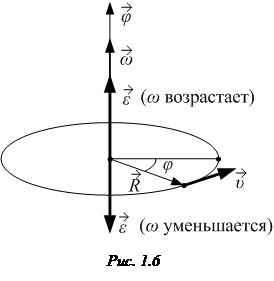
· Положение твердого тела (при заданной оси вращения) определяется углом поворота 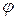(или угловым перемещением 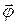, рис. 1.6).

· Кинематическое уравнение вращательного движения:

.

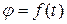· Средняя угловая скорость:

,

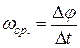где 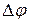– угол поворота за интервал времени .

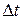· Мгновенная угловая скорость:

.

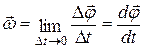· Угловое ускорение:

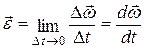; или .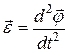

Угловая скорость и угловое ускорение являются аксиальными векторами, их направления совпадают с осью вращения (рис. 1.6).

· Связь между угловыми и линейными величинами

– угол поворота φ и путь S, пройденный точкой по дуге окружности радиусом R:

;

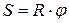– угловая скорость 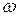и линейная скорость :

, ;

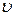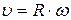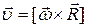– угловое ускорение 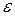и тангенциальное (касательное) ускорение :

, ;

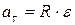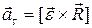– нормальное ускорение 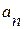, угловая скорость 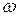и линейная скорость :

, .

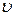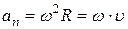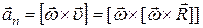· При равномерном вращении , .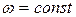

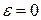· Кинематическое уравнение равномерного вращения:

,

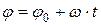где 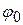– начальная угловая координата; t – время.

· Частота вращения:

,

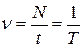где N – число оборотов, совершаемых телом за время t ( 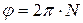); Т – период вращения (время одного полного оборота).

· Связь угловой скорости с периодом и частотой:

.

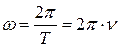· При равнопеременном вращательном движении .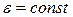

· Угловая скорость при равнопеременном вращении:

,

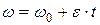где 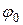– начальная угловая координата; 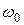– начальная угловая скорость, t – время, ε – угловое ускорение.

· Кинематическое уравнение равнопеременного вращения ( ):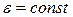

.

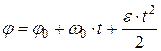Динамика материальной точки

· Второй закон Ньютона (уравнение движения материальной точки):

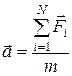, или ,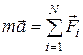

где 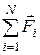– равнодействующая всех N сил, приложенных к телу (векторная сумма всех сил), m – его масса, 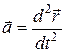– его ускорение.

· Второй закон Ньютона в импульсной форме:

,

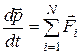где 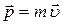– импульс тела (материальной точки), 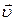– его скорость.

Если сила 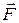, действующая на тело, постоянна, то

,

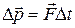где 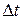– промежуток времени, в течение которого действовала сила 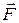; 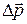– изменение импульса тела.

· Второй закон Ньютона в проекциях:

; ; ,

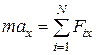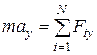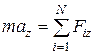или

; ; ,

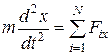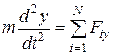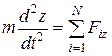где под знаком суммы стоят проекции силна соответствующие оси координат.

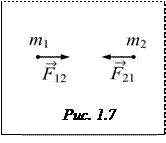
· Третий закон Ньютона (рис. 1.7):

.

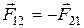· Закон всемирного тяготения (сила гравитационного притяжения):

,

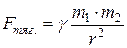где 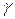– гравитационная постоянная; m₁ и m₂ – массы взаимодействующих тел, рассматриваемые как материальные точки; r – расстояние между ними.

· Сила тяжести

,

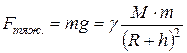где 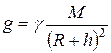– ускорение свободного падения, M – масса Земли, R – радиус Земли, h – высота тела массой m над Землёй.

· Вес тела – сила, приложенная к подставке или подвесу (рис. 1.8). Вес тела, движущегося с ускорением 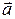, равен

,

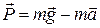где m – масса тела. Если ускорение тела направлено вертикально вверх, то вес 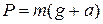; а если вертикально вниз, то .

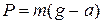· Сила трения скольжения(рис. 1.9):

,

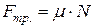где 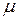– коэффициент трения, N – сила нормального давления.

· Сила трения покоя:

.

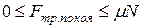· Сила упругости (закон Гука):

,

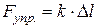где k – коэффициент упругости (жесткость пружины), 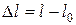– абсолютная деформация (рис. 1.10).

· Радиус-вектор 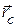и координаты центра масс системы материальных точек:

;

, , ,

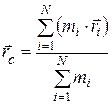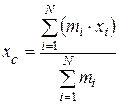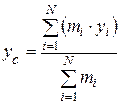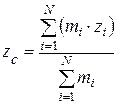где 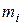– масса i-той материальной точки; 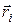, , 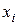, 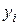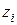– её радиус-вектор и координаты; 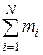– масса всей системы; N число точек.

· Плотность тела:

.

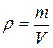· Уравнение движения центра масс:

,

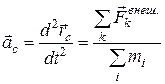где 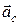– ускорение центра масс; 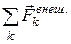– сумма всех внешних сил, приложенных к системе.

· Закон сохранения импульса: если сумма внешних сил равна нулю, то полный импульс системы сохраняется.

Если 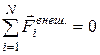, то ,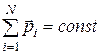

ил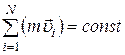и , или .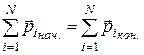

где N – число материальных точек (или тел), входящих в систему.

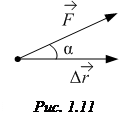
· Работа, совершаемая постоянной силой :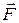

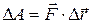, или ,

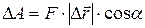где 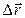– перемещение, 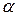– угол между направлениями векторов силы 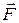и перемещения 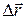(рис. 1.11):

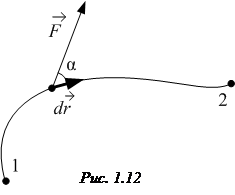
· Работа, совершаемая переменной силой :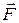

,

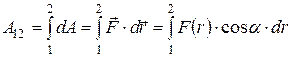где интегрирование производится вдоль траектории (рис. 1.12).

· Средняя мощность за интервал времени :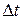

.

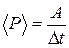· Мгновенная мощность:

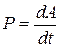, или ,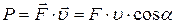

где 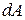– работа, совершаемая за промежуток времени 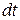, 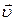– скорость тела, 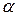– угол между скоростью и силой.

· Коэффициент полезного действия

.

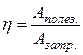· Закон изменения полной энергии для незамкнутой системы:

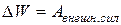, или W_полн.1=W_полн.2+А_{системы против внешних сил}

· Закон изменения механической энергии для незамкнутой системы:

W_мех.1=W_мех.2+А_{системы против внешних сил}+А_{системы против диссипативных сил}

· Кинетическая энергия материальной точки (или тела), движущейся поступательно:

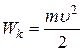, или .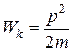

· Потенциальная 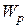энергия тела и консервативная сила, действующая на тело в данной точке поля, связаны соотношением:

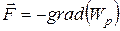, или .

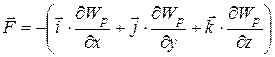В проекциях: , , .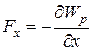

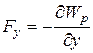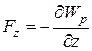Здесь 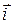, 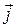и 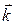– единичные векторы (орты). В частном случае, когда поле сил обладает сферической симметрией (как, например, гравитационное),

.

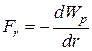· Закон сохранения полной энергии:

Если 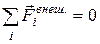, то .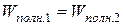

Здесь 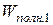и 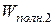– полная энергия системы; сумма всех видов энергии для начального и конечного состояния системы соответственно.

· Закон сохранения механической энергии (выполняется в замкнутой системе, в которой действуют только консервативные силы):

Если 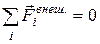и отсутствуют диссипативные силы, то W_мех.1=W_мех.2 .

Здесь 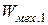и 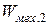– полная механическая энергия системы; сумма всех видов потенциальной и кинетической энергии для начального и конечного состояния системы соответственно ( ).

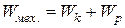· Потенциальная энергия упруго деформированного тела (сжатой или растянутой пружины)

,

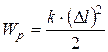где k – жёсткость пружины, 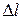– абсолютная деформация.

· Потенциальная энергия гравитационного взаимодействия

,

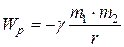где r – расстояние между двумя точечными массами m₁, и m₂, 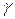– гравитационная постоянная.

· Потенциальная энергия тела в однородном поле силы тяжести:

,

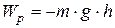где h – высота тела над уровнем, принятым за нулевой, g – ускорение свободного падения. Эта формула справедлива при условии 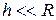, где R – радиус Земли.