Ен.01 элементы высшей математики.

ЕН.01 ЭЛЕМЕНТЫ ВЫСШЕЙ МАТЕМАТИКИ.

1.

Понятие предела функции в точке. Теоремы о пределах. Виды пределов

Ответ:

Предел функции в заданной точке — такая величина, к которой стремится значение рассматриваемой функции при стремлении её аргумента к данной точке.

теоремы:

Если значения функций в окрестности некоторой точки равны, то и их пределы в этой точке совпадают

Если функция имеет предел, то он единственный.

Предел константы равен этой константе

Непрерывность функции в точке и на промежутке. Точки разрыва функции

Ответ:

Функция называется непрерывной в точке, если она определена в этой точке и бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции.

Функция называется непрерывной на интервале, если она непрерывна в каждой точке этого интервала.

Все точки разрыва функции разделяются на точки разрыва первого и второго рода.
функция имеет точку разрыва первого рода при, если в это точке существуют левосторонний предел и правосторонний предел, эти односторонние пределы конечны.
Функция имеет точку разрыва второго рода при, если по крайней мере один из односторонних пределов не существует или равен бесконечности.

Раскрытие неопределенностей

Ответ:

Неопределенность типа 𝟎𝟎

Пусть заданы две функции f(x) и g(x) , такие, что

𝐥𝐢𝐦𝒙→𝒂𝐟(𝐱)=𝟎 и 𝐥𝐢𝐦𝒙→𝒂𝐠(𝐱)=𝟎

В этом случае говорят, что функция 𝒇(𝒙)𝒈(𝒙) имеет неопределённость 𝟎𝟎 в точке x=a. Чтобы найти предел при х=а, когда функция 𝒇(𝒙)𝒈(𝒙) содержит неопределённость 𝟎𝟎, нужно разложить на множители численность и/или знаменатель и затем сократить члены, стремящиеся к нулю. Примечание: В данном разделе при вычислении пределов не используется правило Лопиталя.

Неопределенность типа ∞∞

Пусть две функции f(x) и g(x) обладают свойством

𝐥𝐢𝐦𝒙→𝒂𝐟(𝐱)=±∞ и 𝐥𝐢𝐦𝒙→𝒂𝐠(𝐱)=±∞

Где a является действительным числом, либо стремится к + или -∞. В Этом случае функция имеет в точке а неопределённость типа ∞∞. Для вычисления предела в этой точке необходимо разделить числитель и знаменатель на x в наивысшей степени.

Неопределенности типа ∞−∞, 0*∞, ∞^0, 1^∞

Неопределённости этих типов сводятся к рассмотренным выше неопределённостям типа 𝟎𝟎 и ∞∞.

5.

6.Асимптоты графика функции

Ответ:

Асимптота – это прямая, к которой неограниченно близко приближается график функции при удалении его переменной точки в бесконечность.

1) Вертикальные асимптоты, которые задаются уравнением вида 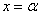, где «альфа» – действительное число. Популярная представительница 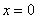определяет саму ось ординат, вспоминаем гиперболу .

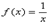Таким образом, чтобы установить наличие вертикальной асимптоты 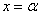в точке x=0 достаточно показать, что хотя бы один из односторонних пределов 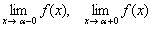бесконечен. Чаще всего это точка, где знаменатель функции равен нулю.

2)Наклонные асимптоты традиционно записываются уравнением прямой с угловым коэффициентом 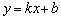. Иногда отдельной группой выделяют частный случай – горизонтальные асимптоты 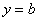. Например, та же гипербола с асимптотой 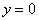.Наклонные (как частный случай – горизонтальные) асимптоты могут нарисоваться, если аргумент функции стремится к «плюс бесконечности» или к «минус бесконечности». Поэтому график функции не может иметь больше двух наклонных асимптот. 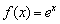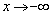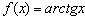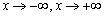Например, график экспоненциальной функции обладает единственной горизонтальной асимптотой при , а график арктангенса при – двумя такими асимптотами, причём различными. Когда график и там и там сближается с единственной наклонной асимптотой, то «бесконечности» принято объединять под единой записью 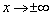. Например,: .

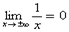Общее практическое правило:Если существуют два конечных предела 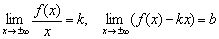, то прямая 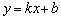является наклонной асимптотой графика функци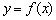и при 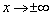. Если хотя бы один из перечисленных пределов бесконечен, то наклонная асимптота отсутствует.

3) Горизонтальные асимптоты

Если существует конечный предел 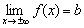, то прямая 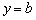является горизонтальной асимптотой графика функци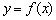и при .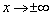

Нетрудно заметить, что числитель и знаменатель функции 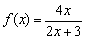одного порядка роста, а значит, искомый предел будет конечным:

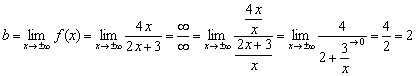
Поведение на бесконечности

Исследуем поведение функции на бесконечности, то есть при .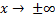

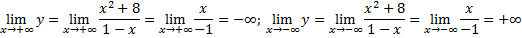
7.

8.

9.

10.

11.

12.

13.

14.Возрастание и убывание функций.

Ответ:

Определение возрастающей функции: Функция 𝑓(𝑥) называется возрастающей на некотором интервале, если для любых двух точек 𝑥1 и 𝑥2 этого интервала, таких что 𝑥1<𝑥2, справедливо 𝑓(𝑥1)<𝑓(𝑥2). Другими словами, большему значению аргумента соответствует большее значение функции.

Определение убывающей функции: Функция 𝑓(𝑥) называется убывающей на некотором интервале, если для любых двух точек 𝑥1 и 𝑥2 этого интервала, таких что 𝑥1<𝑥2, справедливо 𝑓(𝑥1)>𝑓(𝑥2). Другими словами, большему значению аргумента соответствует меньшее значение функции.

Исследование функции

Ответ:

Чтобы исследовать функцию y = f(x) и построить ее график необходимо:

1) найти область определения функции, то есть множество всех точек для которых существует значение функции;

2) найти (если они существуют) точки пересечения графика с координатными осями. Для этого нужно в уравнение 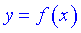подставить аргумент а также решить уравнение 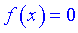для отыскания точек пересечения с осью ;

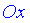3) исследовать функцию на периодичность, четность и нечетность. В некоторых случаях это можно сделать визуально по самому виду функции, если нет, то провести проверку:

1. 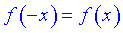– функция четная;

2. 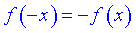– функция нечетная;

3. 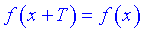– функция периодическая, 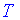– период функции.

Таким образом, если имеем парную функцию 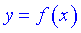то достаточно построить ее для положительных значений 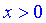, после чего отразить ее симметрично относительно оси абсцисс на другую часть. В случае нечетной функции график будет симметричен относительно начала координат. Например, если имеет нечетную функцию график которой принадлежит первой четверти вторую половину получим поворотом первой четверти на 180 градусов (третья четверть).

Периодическими являются преимущественно функции, составленные из простых тригонометрических и некоторые параметрически заданные функции.

4) найти точки разрыва и исследовать их (такими точками являются края интервалов определения функции);

5) найти интервалы монотонности, точки экстремумов и значения функции в этих точках;

6) найти интервалы выпуклости, вмятины и точки перегиба;

7) найти асимптоты кривой;

8) построить график функции.

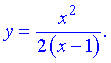
1) Функция определена по всюду кроме точки, в которой знаменатель превращается в ноль ( 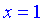). Область определения состоит из двух интервалов

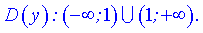
2) При подстановке значения получим

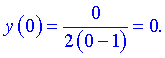
Такую же точку получим если приравняем функцию к нулю. Точка - единственная точка пересечения с осями координат.

3) Проверяем функцию на четность

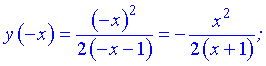
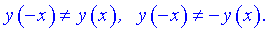
Итак функция ни четная, ни нечетная, непериодическая.

4) В данном случае имеем одну точку разрыва 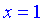. Вычислим границы слева и справа от этой точки

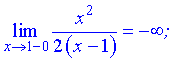
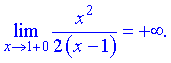
Итак 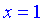– точка разрыва второго рода.

5) Для отыскания интервалов монотонности вычисляем первую производную функции

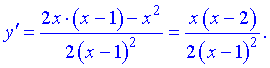
Приравнивая ее к нулю получим точки подозрительные на экстремум 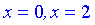. Они разбивают область определения на следующие интервалы монотонности

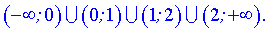
Исследуем поведение производной слева и справа от найденных точек разбиения

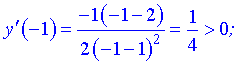
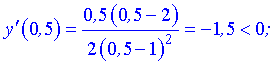
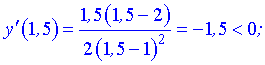
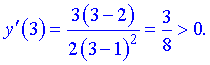
Графически интервалы монотонности будут иметь вид

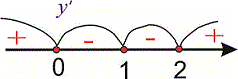
Исследуемая функция возрастает на интервалах 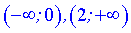и убывает .

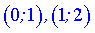Точка – точка локального максимума, 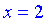– локального минимума. Найдем значение функции

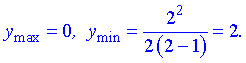
6) Для отыскания интервалов выпуклости найдем вторую производную

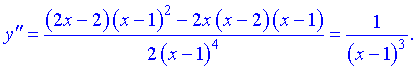
Таких интервалов нет, поскольку вторая производная не принимает нулевых значений в области определения.

7) Точка 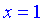– вертикальная асимптота функции. Уравнение наклонной асимптоты имеет вид

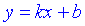
где 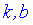- границы которые вычисляются по правилу

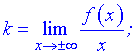
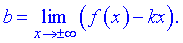
Находим нужные границы

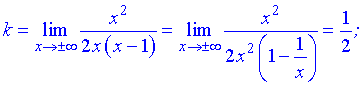
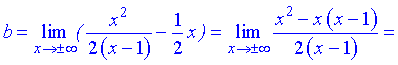
Конечный вид прямой следующий

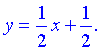
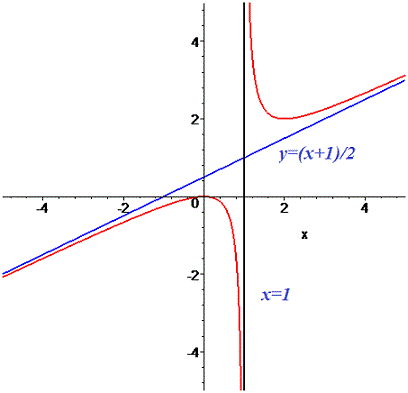
8) На основе проведенного анализа выполняем построение графика функции. Для этого сначала строим вертикальные и наклонные асимптоты, затем находим значение функции в нескольких точках и по них проводим построение.

18.

Метод подстановки

Ответ:

Сущность этого метода заключается в том, что путём введения новой переменной интегрирования удаётся свести заданный интеграл к новому интегралу, который сравнительно лёгко берётся непосредственно.

Пусть дан интеграл ∫f(x)dx, который не является табличным.

Записываем уравнение замены

y=y(x)

Находим дифференциал этой функции

.dy=y’(x)dx

Выражаем

dx=(dy)/(y’(x)).

Подставим в данный интеграл:

∫f(x)dx= ∫g(y)dy

Находим

. ∫g(y)dy=F(y)+C

Чтобы получить окончательный ответ, вместо переменной y подставляем y(x) выражение :

∫f(x)dx+F(y(x))+C

27.

28.

29.

32.

33.

34.

ЕН.01 ЭЛЕМЕНТЫ ВЫСШЕЙ МАТЕМАТИКИ.

1.