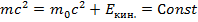Кинематика относительного движения. Сила инерции в общем случае.

Пусть дана неподвижная система S и S’ – подвижная система.Радиу-вектор точки 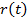в системе S обозначим 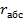, r₀-радиус вектор подвижной системы, r’-радиус—вектор точки m относительно системы S’. Тогда

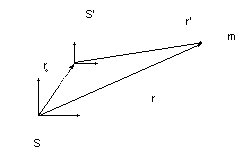
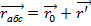
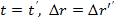
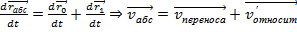
a) 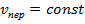Система совершает равномерное поступательное движение.

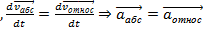Обе системы инерциальные и законы механики 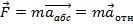- одинаковы.

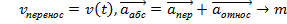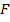b) система движется с ускорением, тогда a_отн= --ma_пер Таким образом, к действующей силе F в неинерциальной системе S’ добавляется некоторая сила 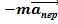,связанная только с ускоренным движением системы. Это по определению сила инерции. Итак,если

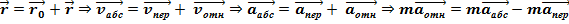,то

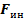= – m 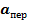Это сила инерции поступательного движения.

в) Пусть система S’ вращается вокруг неподвижной оси с угловой скоростью 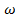,. Т.е она движется с нормальным ускорением. Тогда на неподвижное тело в этой системе также будет действовать сила инерции, которую можно найти по общему правилу: 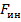= – =– 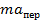m = –m 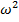r– это центробежная сила инерции.

г) . Пусть система движется поступательно со скоростью 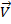и вращается с угловой скоростью 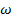вокруг неподвижной оси ( т.е движется произвольно). Тогда по принципу суперпозиции движения полная скорость системы: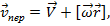 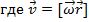-это составляющая вектора скорости, связанная с вращением. Пусть далее все параметры движения ( 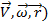есть функции времени. По правилу сложения векторов ускорений:

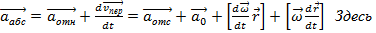
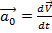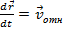, - скорость движения тела m, относительно системы S’: можно заменить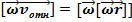

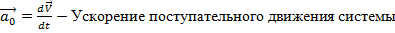. Порождает поступательную силу инерции 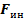= – m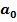

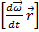ускорение, связанное с неравномерностью вращение системы. При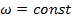

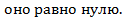Сила инерции 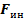= – m 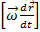-состоит из двух составляющих: центробежной силы инерции, связанной только с вращением тела (с изменением радиуса-вектора точки по направлению) и силы инерции Кориолиса, связанной с движением тела, относительно подвижной системы (с изменением радиуса-вектора точки по величине).

=

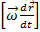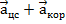
Теорема Кориолиса.

Абсолютное ускорение тела есть векторная сумма ускорений: относительного, переносного и кориолисова .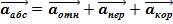

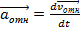
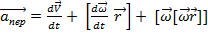Здесь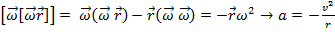

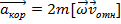
То есть .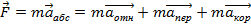

S’: 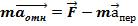- m 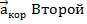закон динамики тела в S'.

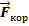= – 2m[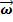 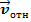],сила перпендикулярна к веторам скоростей.

Примеры:

1. Поступательная сила инерции. Пусть в системе S' находится математический маятник.

За ним наблюдают два наблюдателя: S- всегда неподвижен и S’- может двигаться. Механизм в покое 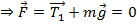.Сила натяжения и вес уравновешиваются. Оба наблюдателя по первому закону подтверждают это.

Теперь двинем систему с 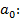Наблюдатель S: нить должна отклониться, чтобы результирующая сила F сообщила телу ускорение 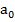.Для наблюдателя S’ маятник в покое, но отклонился так, что вес и натяжение не уравновешивают друг друга, он вынужден приписать ещё одну силу –ma₀ чтобы удовлетворить первому закону механики.

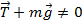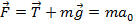, - с точки зрения S, а с точки зрения S’ существует сила инерции: 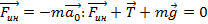– тогда маятник в покое.

2. Центробежная сила инерции Маятник вращается вокруг неподвижной оси. Для S- наблюдателя- при отклонении результирующая сила меняет направление вектора скорости. Для наблюдателя S’-вновь нужно ввести силу от оси вращения, чтобы сумма сил равнялась нулю и тогда выполниться первый закон.

Проявление сил инерции в движениях на Земле:

1) Меняется ускорение силы тяжести .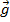

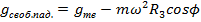
2) Форма земли – геоид. Составляющая ц.б. силы инерции сдвигает массу Земли к экватору.

3) Волга движется вверх также вследствие действия сил инерции.

4) 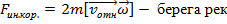, пассаты и муссоны.

Раздел 7. Элементы теории относительности. Примеры.

Как и многие научные теории - теория относительности (ТО) строится на постулатах.

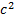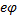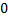1. Скорость света в вакууме не зависит от

скорости движения источника или приемника

т.е. скорость света С=const.

Эксперимент с электронами показал, что

максимальная скорость их движения не превышает «с», хотя энергия их растёт пропорционально работе источника: Объяснение кроется в зависимости массы от скорости.

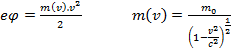
2. Все законы физики выполняются во всех инерциальных системах, то есть все наблюдатели S равноправны.

’

’

’

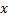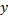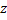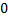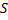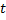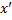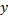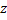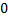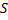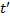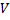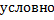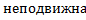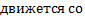В t = 0 S и S’ находятся в одной точке, потом происходит движение.

Разместим лампочку в 0. Фронт волны в S: 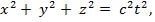Фронт сфера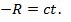

В S’ такой фронт волны – сфера: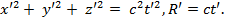

При переходе из S в S’: равноправие наблюдателей удовлетворяется, если и координаты и время подвергнуть преобразованиям: y’=y; z’=z;

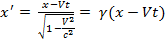(1), где 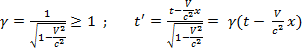(2)

При переходе из S’ в S: y=y’; z=z’;

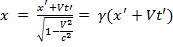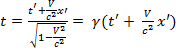(3) (4).

1) Если 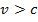, то x, t – мнимые, следовательно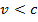

2) Если найти 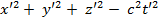с учётом (1) и (2), то получим 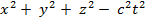. Таким образом удовлетворяем второму постулату.

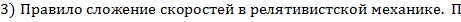родифференцируем (3) и(4):

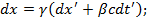dt= 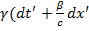). Здесь 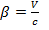Найдём скорость: = .

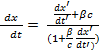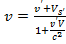4) Сокращение длины. Пусть в S есть линейка 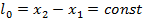, 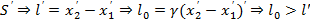- длина не сохраняется.– длина покоящейся больше движущейся. Лоренцево сокращение длины. Аналогично линейка в S’измеренная покоящимся наблюдателем = ( - )=

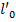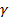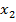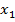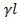
4).Замедление времени. В системе S.в одном месте X = const; событие длится от 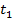до 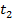.Интервал

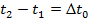.За этим событием наблюдает S’по своим часам 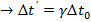, то есть 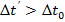и наоборот. X’ = const, S’: 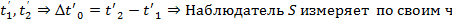асам

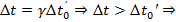интервал времени в системе движущейся, больше, чем в покое.

5).События, происходящие в одной точке в системе S в разные промежутки времени -в S' различны и во времени и в пространстве.

6) Закон сохранения массы. 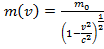разложим в ряд (бином Ньютона). Для первых двух членов ряда: 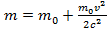= 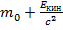; В замкнутой системе сохраняется полная масса тел,

Этот закон позволяет превращать частицу с меньшей массой покоя в частицу с большей массой.

7). Закон сохранения релятивистской энергии: