Закон всемирного тяготения. Гравитационное поле. Гравитационная энергия. Гравитационный радиус.
Считается, что законы Кеплера послужили экспериментальной основой ля вывода закона тяготения.
Законы Кеплера:
1) все планеты движутся по эллиптическим траекториям, в одном из фокусов которого Солнце.
2) за любые равные промежутки времени радиус-вектор планеты описывает одинаковую площадь,
то есть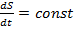 
3) отношение квадратов периода вращения планет к кубу длин больших полуосей одинаков для всех планет: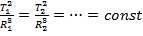 
.
Покажем, что законы Кеплера могут быть использованы для вывода закона всемирного тяготения.
Предположим, что все орбиты круговые и так как вектор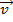 
направлен то касательной к траектории, то 
. 
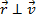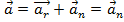, где 
, так как движение равномерное.
 |
 |
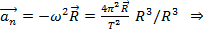
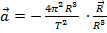, где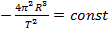 
согласно третьему закону Кеплера.
Таким образом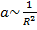 
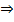
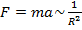
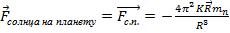. По третьему закону Ньютона: 
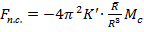. Следовательно 
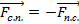. Таким образом, 
=> 
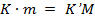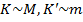
Ньютон предположил, что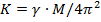 
, где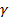 
- гравитационная постоянная.
Таким образом,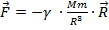 
– закон тяготения между планетами солнца. Ньютон также предположил, что все тела во вселенной испытывают притяжения друг к другу. Для точечных тел закон всемирного тяготенияимеет вид: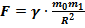 
Эта сила прямо пропорциональна произведению их масс точечных тел и обратно пропорциональна квадрату расстояний между ними.
Особенности: 1) Силы тяготения всегда силы притяжения;
2) не зависят от физической (химической) природы тела;
3)в силу малости гравитационной постоянной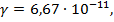 
гравитационные силы имеют значимое значение для больших масс. 
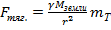=g 
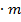. где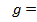 
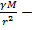ускорение силы тяжести. Таким образом, для небольших высот 
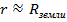, тогда 
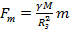, ускорение силы тяжести Земли одинаково для всех тел. (Закон справедлив и для тел сферической формы).
4) Сравним закон тяготения со вторым законом Ньютона: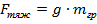 
, 
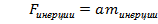
Одинакова ли масса гравитационная и инерционная? Было показано с точностью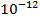 
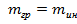
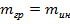
Принцип эквивалентности:
Если есть система, движущаяся с ускорением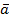 
и находящаяся в гравитационном поле, то исследователь, находящийся в этой системе, не может определить, какая часть сил обусловлена гравитационными силами , а какая – ускоренным движением системы.
Ньютон не стал давать объяснения физической природы гравитационных сил, назвав их силами дальнодествия. Соврененая теория- это теория полевого взаимодествия материальных тел.
Полевая теория
Любое тело создает вокруг себя поле – гравитационное поле.
Свойства гравитационного поля:
1) Оно непрерывно распределено в пространстве, проникает в другие поля и вещества.
2) Это поле действует с некоторой силой на все тела, помещенные в это поле.
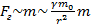
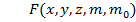– сила тяготения зависит не только от выбора точки поля (x,y,z) и массы тела, создающего поле ( 
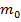,) , но и от массы «пробного» тела (m), что крайне не удобно для характеристики поля. Поэтому введем другую величину.
Напряженность гравитационного поля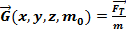 
- -численно равна силе, дейсвующей на единичную массу, помещённую в данную точку поля. Тогда закон примет вид:
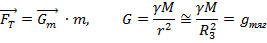
1) Поле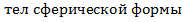 
имеет точно такую же структуру, что и точечное тело такой же массs M, помещенной в центре сферы. (для 
)
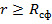2) Это поле цетральное (поле центробежных сил.)
То есть поле потенциально, то:
1) работа сил поля A зависит только от начальной и конечной точки, а не от траектории.
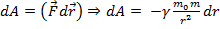Знак минус т.к. угол между силой и радиус-вектором 
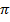Тогда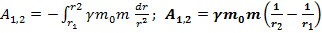 
2) Так как работа равна изменению энергии,то имеет смысл разность потенциальных энергий
тела в двух точках поля:
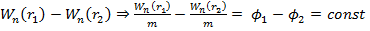Найдём эту энергию через работу
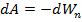
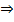
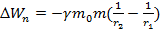. Тогда 
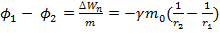-разность потенциалов двух точек гравитационного поля: численно равна работе сил поля по перемещению единичной массы из первой точки во вторую.
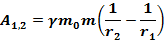
1. Если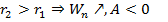 
Тело удаляется, работа совершается против сил поля (притяжения). Работа отрицательна, потенциальная энергия растет.
2. Если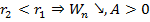 
. Тела сближаются силами поля, работа положительна, потенциальная энергия уменьшается.
3. Если принят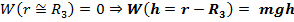ь: 
Здесь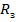 
-радиус Земли.
Так как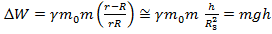 
.
4. 
= 
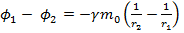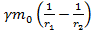
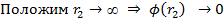Тогда потенциал произвольной точки поля :
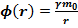–относительно бесконечности: численно равен работе, которую нужно совершить, чтобы единичную массу перенести из данной точки в бесконечность.
Определим энергии гравитационного поля 
.
Пусть имеем шар массы 
и радиусом-R. Энергию гравитационного поля шара можно определить как работу по переносу всей массы тела в бесконечность. Так как потенциал поверхности будет меняться с изменением размеров шара (и его массы), то следует переносить массу б.малыми порциями dm. Тогда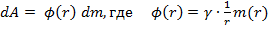 
-текущее значение потенциала поверхности шара. Выразим m(r):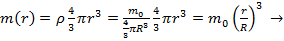 
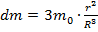dr и можно записать в явном виде: 
.
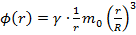Подставляя в выражение для работы: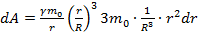 
=> 
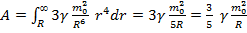Таким образом 
, 
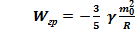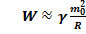
Примеры
1. Считая, что полная энергия электрона равна его гравитационной, получим: 
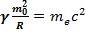
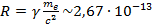см – совпадает с другими методами вычислений. 2..Применим последнюю формулу к произвольному гравитационному объекту:
= 
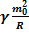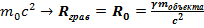Это гравитационный радиус объекта.
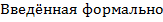величина 
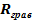оказалась чрезвычайно информативной и важной.
1) Можно оценить гравитационную энергию объекта.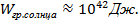 
(Посчитав плотность энергии, излучаемой Солнцем , учёные пришли к выводу о наличии еще каких- то источников энергии , в частности, энергию термоядерной реакции.
2) Если сравнить истинный радиус планеты и её гравитационный радиус, то при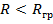 
, с планеты нельзя излучать никакие виды энергии ( в том числе и свет). То есть, мы эту планету не увидим. Следовательно, возникает ЧЁРНАЯ ДЫРА.
 |
 |
 |
 |
 |
 |
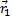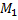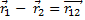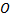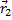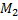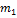и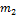 
. Одно движется в гравитационном поле другого от точки отсчета проведены радиус-векторы.
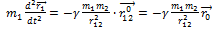, где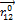 
- единичный вектор.
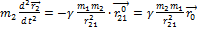
Начальные условия: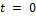 
, 
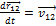, еще наложить условия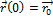 
Вычтем: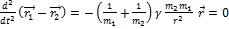 
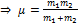– приведённая масса, тогда
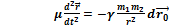- уравнение движения одного тела, относительно другого.
Решение этого уравнения достаточно сложное. Для качественных оценок можно использовать
законы сохранения:
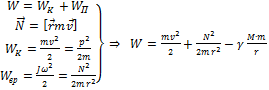Здесь два последних слагаемых есть функции координат (r) т.е потенциальная энергия- 
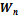,(Так как N = const по закону сохранения момента импульса
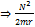функция от r)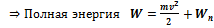 
Замечания Качественный анализ.
1) 
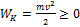кинетическая энергия тела может быть только положительной
: 
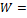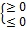но полное не может быть меньше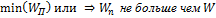 
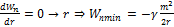
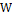
1. 
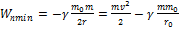- для частицы с массой m.
Единственное решение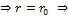 
движение строго по окружности с 
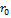. r
2. 
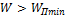, то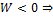 
существует два решения в некотором интервале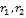 
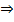движение по эллипсу.
3. 
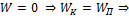движение по параболе (разомкнута относительно ).
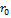4. 
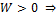движение по гиперболе (разомкнута вообще).