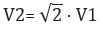Что такое потенциальная энергия? Что такое начало отсчета потенциальной энергии?

Потенциальная энергия— это энергия, которая определяется взаимным положением взаимодействующих тел или частей одного и того же тела.

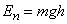
Начало отсчета потенциальной энергии- точка, в которой потенциальная энергия частицы считается равной нулю. Её можно выбирать произвольно.

По какой формуле вычисляется потенциальная энергия силы тяготения двух тел?

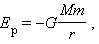где M – масса Земли, G – гравитационная постоянная

По какой формуле вычисляется потенциальная энергия силы тяжести МТ и системы МТ?

E_р =mgh

Потенциальную энергию системы (E_p) можно разделить на внешнюю: (E_p^vnesh) и внутреннюю потенциальные энергии E_p^vnesh . Тогда:

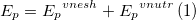
где E_p^vnesh получается как результат воздействия на систему со стороны тел, которые в рассматриваемую систему не входят. E_p^vnutr – вызвана взаимодействием разных частей составляющих систему.

E_p^vnutr является функцией координат всех материальных точек системы; E_p^vnesh помимо координат может в явном виде зависеть от времени.

По какой формуле вычисляется потенциальная энергия силы упругости?

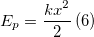
Где k – коэффициент упругости.

Что такое потенциальное поле?

Потенциальное поле — поле, в котором работа, совершаемая силами при перемещении тела из одного положения в другое, не зависит от того, по какой траектории это перемещение произошло, а зависит только от начального и конечного положений.

Что такое полная механическая энергия МТ?

Полной механической энергией тела называют сумму его кинетической и потенциальной энергий.

Что такое полная механическая энергия системы МТ?

Полная механическая энергия Е незамкнутой системы материальных точек – это сумма потенциальной энергии U системы и общей кинетической энергии T всех элементов системы в данный момент времени, то есть

E = U + T.

Как связано изменения полной механической энергии МТ с работой неконсервативных сил?

Как связано изменения полной механической энергии системы МТ с работой неконсервативных сил?

Сформулируйте закон сохранения полной механической энергии системы МТ.

Закон сохранения механической энергии состоит в том, что полная механическая энергия замкнутой системы остается неизменной, т.е. сумма потенциальной и кинетической энергии тела, остается постоянной, если действуют только силы упругости и тяготения и отсутствуют силы трения.

Для замкнутой системы физических тел, например, справедливо равенство
E_k1 + E_p1 = E_k2 + E_p2,
где E_k1, E_p1 — кинетическая и потенциальная энергии системы какого-либо взаимодействия, E_k2, E_p2 — соответствующие энергии после.

Закон сохранения энергии — это интегральный закон. Это значит, что он складывается из действия дифференциальных законов и является свойством их совокупного действия.

Приведите выражения для первой и второй космической скорости.

Первая космическая скорость

Это скорость физического объекта, с которой он может вращаться вокруг Земли, не падая на нее и не отрываясь в пространство. Первая космическая скорость обеспечивает равновесное положение тела, движущегося по круговой траектории вблизи поверхности Земли. При отсутствии тормозящих факторов такое движение может продолжаться бесконечно долго. При этом масса самого вращающегося объекта значения не имеет, а радиус окружности вращения должен немного превышать радиус Земли.

Центробежная сила вычисляется по формуле:

С = mvv/r

m – масса точки
v – линейная скорость точки
r – радиус траектории

Сила притяжения Земли вычисляется по формуле:

С = GМм/rr

G – гравитационная составляющая
М – масса Земли = 5,97•1024 кг
r – радиус Земли = 6371 км

Тогда равновесную скорость вращения объекта (первую космическую скорость) можно найти из уравнения:

mvv/r = GМм/rr

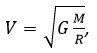где V – первая космическая скорость; G – гравитационная постоянная; M – масса объекта; R – радиус объекта

Вторая космическая скорость

Это минимальная скорость, при достижении которой объект, движущийся по вращательной орбите вокруг Земли, может преодолеть силу притяжения планеты и улететь в пространство. Её еще называют скоростью убегания. Для каждого небесного тела она своя, для планеты Земля равна 11,18 км/с над поверхностью Земли.

Можно рассчитать, используя следующую формулу:

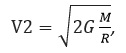где V – первая космическая скорость; G – гравитационная постоянная; M – масса объекта; R – радиус объекта;

Но если известна первая космическая скорость исследуемого объекта (V1), то задача облегчается в разы, и вторая космическая скорость (V2) быстро находится по формуле: