Общие теоремы динамики для материальной точки, системы и твердого тела
Общие теоремы динамики для материальной точки, системы и твердого тела
Количество движения
Количеством движения материальной точки 
называется вектор, равный произведению массы точки 
на ее скорость 
. 
Проекции количества движения точки на прямоугольные декартовы оси координат равны:
, 
, 
Количеством движения системы материальных точек 
называется векторная сумма количеств движений отдельных точек системы.
Единицей измерения количества движения в СИ является – 
Количество движения системы можно выразить через массу системы и скорость центра масс. 
В проекциях на оси координат:
, 
Элементарный и полный импульс силы
Действие силы 
на материальную точку в течении времени 
можно охарактеризовать элементарным импульсом силы 
.
Полный импульс силы за время 
, или импульс силы 
, - это вектор, который определяется по формуле 
. (Полный интеграл за время от элементарного импульса).
В частном случае, если сила постоянна и по величине , и по направлению ( 
), 
.
Проекции импульса силы на прямоугольные декартовы оси координат равны:
Единицей измерения импульса в СИ является – 
Теорема об изменении количества движения
Теорема об изменении количества движения точки
Теорема. Первая производная по времени от количества движения точки равна равнодействующей активных сил и реакций связей, действующих на материальную точку.
Запишем основной закон динамики 
в виде 
. Так как масса постоянна, то внесем ее под знак производной.
Тогда 
, или 
(*)
В проекциях на координатные оси уравнение (*) можно представить в виде:
Теорема импульсов (в дифференциальной форме). Дифференциал от количества движения точки равен элементарному импульсу силы, действующей на точку.
Умножим левую и правую части уравнения (*) на и получим
(**)
В проекциях на координатные оси получаем:
, 
, 
.
Теорема импульсов (в интегральной форме). Изменение количества движения точки за какой-либо промежуток времени равно импульсу силы за этот же промежуток времени.
Интегрируя обе части уравнения (**) по времени в пределах от нуля до получаем:
В проекциях на координатные оси получаем:
, 
, 
Законы сохранения количества движения
1. Если главный вектор всех внешних сил системы равен нулю (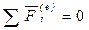 
), то количество движения системы постоянно по величине и направлению.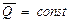 
2. Если проекция главного вектора всех внешних сил системы на какую-либо ось равна нулю (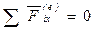 
), то проекция количества движения системы на эту ось является постоянной величиной.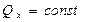 
Теорема об изменении момента количества движения системы относительно центра масс
Для осей движущихся поступательно вместе с центром масс системы, теорема об изменении момента количества движения системы относительно центра масс сохраняет тот же вид, что и относительно неподвижного центра.
Общие теоремы динамики для материальной точки, системы и твердого тела
Количество движения
Количеством движения материальной точки называется вектор, равный произведению массы точки на ее скорость .
Проекции количества движения точки на прямоугольные декартовы оси координат равны:
, ,
Количеством движения системы материальных точек называется векторная сумма количеств движений отдельных точек системы.
Единицей измерения количества движения в СИ является –
Количество движения системы можно выразить через массу системы и скорость центра масс.
В проекциях на оси координат:
,