Графическое изображение гармонических колебаний. Векторная диаграмма.

Решение многих вопросов в теории колебаний значительно упрощается, если использовать графический метод изображения гармонических колебаний в виде векторов на плоскости. Такое изображение называется векторной диаграммой колебаний (Рисунок 20.1).

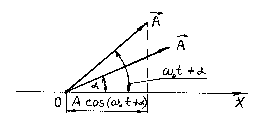
Рисунок 20.1 – Векторная диаграмма гармонического колебаний.

Последовательность построения векторной диаграммы колебания, заданного уравнением 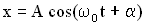, такова:

1. Выберем на плоскости ось Х, на ней возьмем точку О – начало координат.

2. Под углом α, равном начальной фазе колебаний, к оси Х, из точки О откладываем вектор, равный по длине амплитуде А колебаний.

3. Вектор А равномерно вращаем вокруг точки О против часовой стрелки с угловой скоростью, равной циклической частоте 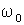колебаний.

Тогда в любой момент времени угол вектора А с осью Х равен 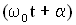. Соответственно проекция конца вектора А на ось Х будет совершать колебания по закону 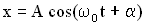, а сама проекция вектора Ав любой момент времени будет равна смещению х колеблющейся точки от положения равновесия. Если начальная фаза колебаний 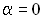, то в начальный момент времени вектор А откладываем из точки О вдоль направления оси Х.

Сложение сонаправленных колебаний с неравными, но близкими частотами.

Частоты складываемых колебаний не равны 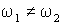, но разность частот 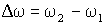много меньше и ω₁, и ω₂. Условие близости складываемых частот записывается соотношениями .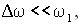

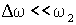Примером сложения сонаправленных колебаний с близкими частотами является движение горизонтального пружинного маятника, жесткость пружин которого немного различна k₁ и k₂.

Пусть амплитуды складываемых колебаний одинаковы 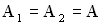, а начальные фазы равны нулю 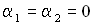. Тогда уравнения складываемых колебаний имеют вид:

, .

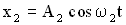Результирующее колебание описывается уравнением:

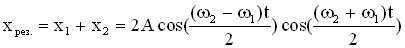. (20.4)

Получившееся уравнение колебаний зависит от произведения двух гармонических функций: одна – с частотой 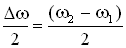, другая – с частотой 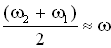, где ω близка к частотам складываемых колебаний (ω₁ или ω₂). Результирующее колебание можно рассматривать как гармоническое колебание с изменяющейся по гармоническому закону амплитудой. Такой колебательный процесс называется биениями.

Биениями называются периодические изменения амплитуды колебания, возникающие при сложении двух гармонических колебаний с близкими частотами.

Строго говоря, результирующее колебание в общем случае не является гармоническим колебанием.

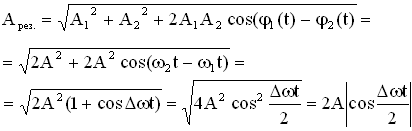
Абсолютное значение косинуса взято потому, что амплитуда – величина положительная или;

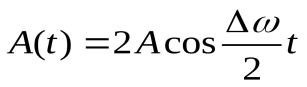(20.5)

Характер зависимости х_рез.при биениях показан на Рисунке 20.3.

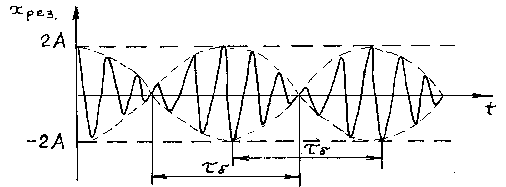
Рисунок 20.3 – Зависимость смещения от времени при биениях.

Амплитуда биений медленно меняется с частотой 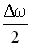. Абсолютное значение косинуса повторяется, если его аргумент изменяется на π, значит и значение результирующей амплитуды повторится через промежуток времени τ_б, называемый периодом биений. Величину периода биений можно определить из следующего соотношения:

.

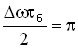Величина 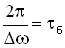- период биений.

Величина 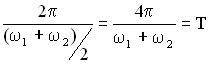есть период результирующего колебания (Рисунок 20.3).