Формула остроградского-гаусса

Если функции P, Q, R непрерывны вместе со своими частными производными первого порядка в замкнутой области V пространства, ограниченного замкнутой гладкой поверхностью S, то справедлива формула Остроградского-Гаусса:

,

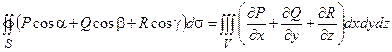или в векторной форме

.

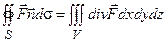Пример 3.3.Летательный аппарат, поверхность S которого задается уравнениями: 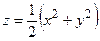, z = 2 (координаты даны в метрах); находится в потоке частиц, движущихся со скоростью 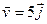(м/c). Вычислить массу частиц m, бомбардирующих боковую поверхность аппарата в единицу времени, если плотность вещества в потоке m= const (кг/м³).

Решение. Масса частиц, бомбардирующих боковую поверхность в единицу времени, определяется как произведение

m=m×П,

где П - поток векторного поля через боковую поверхность S, m - плотность частиц. Поток можно определить разными способами.

Способ 1. Вычислим поток П с помощью поверхностного интеграла (3.8):

.

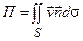Для этого надо найти скалярное произведени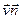е , где - вектор нормали к боковой поверхности, направленный внутрь (рис.3.5). Запишем уравнение боковой поверхности в виде 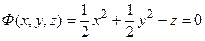, тогда вектор 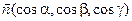найдем по формулам (3.9):

, , ,

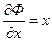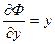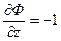Рис. 3.5

, , .

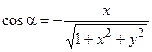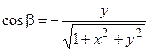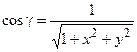Объясним выбор знаков. Вектор направлен внутрь поверхности и образует с осью Oz острый угол, следовательно, направляющий косинус должен быть положителен, cosg > 0. А так как производная 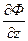отрицательна, то радикал в знаменателе берем со знаком «минус», и в других дробях тоже.

Скалярное произведение векторов скорости и нормали:

.

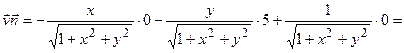
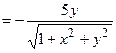При y > 0 скалярное произведение 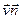отрицательно, т.е. в этой области частицы вылетают из аппарата. Это противоречит условию, так как частицы не проходят сквозь поверхность, а бомбардируют ее. Следовательно, ту часть поверхности, где 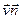< 0, необходимо исключить. Тогда интегрировать будем по той части поверхности S, где у < 0.

Так как 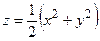, то

.

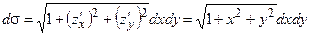Имеем

.

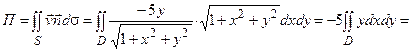
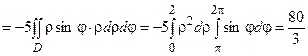Способ 2. Вычислим поток как поверхностный интеграл по координатам (3.7)

.

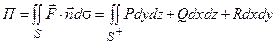Векторное поле имеет координаты P = 0, Q = 5, R = 0, тогда

.

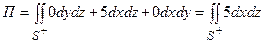Этот поверхностный интеграл приведем к двойному по проекции поверхности S на плоскость xOz по формуле (3.10):

.

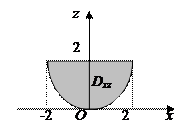
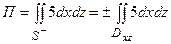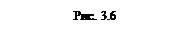Так как поле параллельно оси Oy, то частицы будут бомбардировать только ту часть поверхности, где у < 0. Вектор нормали, направленный внутрь поверхности, образует с осью Oy острый угол, поэтому мы возьмем интеграл с положительным знаком.

.

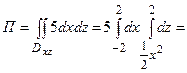
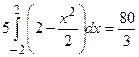Отметим, что не во всех случаях по заданию векторного поля можно увидеть бомбардируемую часть поверхности. Тогда вернее воспользоваться первым способом и определить область, где скалярное произведение 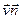положительно. В тех задачах, где поле проникает сквозь поверхность эта операция лишняя и оба метода пригодны.

Ответ: масса частиц .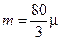

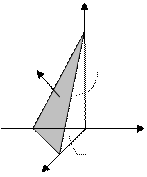z   Dxz   Dyz -2 O y 3 Dxy x

Пример 3.4.Вычислить 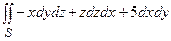по верхней стороне части плоскости 2x – 3y + z = 6, лежащей в четвертом октанте.

Решение. Нормаль , соответствующая указанной стороне поверхности, образует с осью Oy тупой угол, а с осями Ox и Oz – острые. Поэтому в формуле (3.10) берем знаки «плюс», «минус», «плюс» и получаем двойные интегралы по проекциям поверхности на координатные плоскости.

=

.

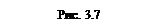
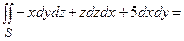
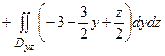
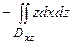
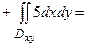
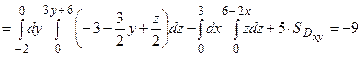Ответ: -9.

ЗАДАНИЕ К КУРСОВОЙ РАБОТЕ

1. Оболочка S летательного аппарата представляет собой полую тонкостенную конструкцию, выполненную из композиционного материала с поверхностной плотностью g(x, y, z) (координаты даны в метрах, поверхностная плотность - кг/м²). Вычислить:

а) массу оболочки m₀;

б) координаты центра тяжести C₀(x_c0, y_c0, z_c0);

в) моменты инерции оболочки относительно координатных осей I_x0, I_y0, I_z0.

2. Укомплектованный, готовый к запуску аппарат можно считать однородным с пространственной плотностью m₁ = const (кг/м³), т.е. массу оболочки не учитывать. Вычислить:

а) массу аппарата m₁;

б) координаты центра тяжести C₁(x_с1, y_с1, z_с1);

в) моменты инерции аппарата относительно координатных осей I_x1, I_y1, I_z1.

3. Летательный аппарат находится в потоке частиц, движущихся со скоростью (x, y, z) (м/c). Вычислить массу частиц m, бомбардирующих боковую поверхность аппарата в единицу времени, если плотность вещества в потоке m₂ = const (кг/м³).

4. Теплота сгорания топлива q =10² МДж/кг, КПД двигателей h= 60%. Рассматривая летательный аппарат как материальную точку, найти массу горючего M, необходимого для перемещения аппарата в силовом поле 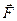(x, y) вдоль траектории L от точки A до точки B (сила 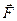дана в килоньютонах, координаты - в километрах).

Данные по вариантам приведены в приложении.

БИБЛИОГРАФИЧЕСКИЙ СПИСОК

1. Пискунов, Н. С. Дифференциальное и интегральное исчисления: в 2 т. / Н. С. Пискунов. – Т. 2. – М.: Наука, 1985.

2. Смирнов, В. И. Курс высшей математики: в 8 т. / В. И. Смирнов. – Т. 2. – М.: Наука, 1965.

3. Шестаков, А. А. Курс высшей математики / А. А. Шестаков. – М.: Высш. шк., 1981.

4. Слободецкий, Л. Н. Интегральное исчисление / Л. Н. Слободецкий. – М.: Высш. шк., 1974.

5. Бронштейн, И. Н. Справочник по математике для инженеров и учащихся втузов / И. Н. Бронштейн, К. А. Семендяев. – М.: Наука, 1980.

6. Данко, П. Е. Высшая математика в упражнениях и задачах: в 2 ч. / П. Е. Данко, А. Г. Попов, Т. Я. Кожевникова и др. – Ч. 2. – М.: Высш. шк., 1980.

7. Письменный, Д. Т. Конспект лекций по высшей математике: в 2 ч. / Д. Т. Письменный. – Ч. 2. – М.: Рольф, 2001.

Приложение

ВАРИАНТЫ ЗАДАНИЙ

№	Поверхность S	Поверх. плотность γ(x, y, z)	Поле скоростей (x, y, z)	Силовое поле (x, y)	Траектория L
	x2 + y2 = 1, z = 2, z = 0	x2	(-x; -y; z)	(x – y; 1)	x2 + y2 = 4, y > 0, A(-2;0), B(2;0)
	, z = 4	y2	(-x; -y; z)	(x –y; x +y)	, y > 0, A(-3;0), B(3;0)
	x2 + y2 + z2 = 4, z > 0	z + 1	(y; -x; 0)	(y2; x)	y = 4x, A(2;8), B(0;0)
	2z = 4 – (x2 + y2), z = 0	x2	(-x; -y; -2z)	(x2y; -y)	отрезок AB, A(-1;0), B(0;1)
	, z = 0	y2	(-x; -y; -z)		y = 2 , A(1;2), B(0;0)
	x2 + y2 = 2z, z = 1/2	x2	(x; y; 2z +10)	(xy - y2; x)	y = 2x2, A(1;2), B(0;0)
	x2 + y2 = z2, z > 0, z = 1	x2	(x - 5; y; z)	(y2 - y; 2xy)	x2 + y2 = 9, y > 0, A(-3;0), B(3;0)
	x2 + y2 + z2 = 9, z > 0	x2	(0; 0; z2 –16)	(xy; 2)	y = sin x, A(π;0), B(0;0)
	y2 + z2 = 10x, x = 10	y2 + z2	(2x +20; y; z)	(x2 + y2; y2)	отрезок AB, A(2;0), B(0;2)