Приложения тройного интеграла

1. Масса тела

Если μ(х, у, z) - плотность вещества, то масса тела, занимающего область Т, вычисляется по формуле

.

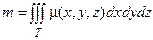2. Статические моменты

Статические моменты тела относительно координатных плоскостей xОy, yОz и xOz вычисляются по формулам:

, ,

.

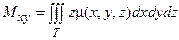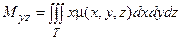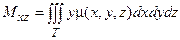3. Координаты центра тяжести

Координаты центра тяжести тела, имеющего плотность μ(х, у, z):

, ,

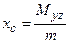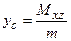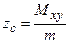
где m - масса тела, М_хy, М_yz, М_хz - ее статические моменты.

Если тело однородное, т.е. μ = const, то эти формулы принимают вид:

, ,

.

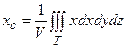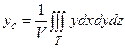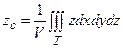4. Моменты инерции

Моменты инерции тела относительно осей Ох, Оу, Oz вычисляются по формулам:

,

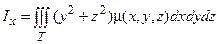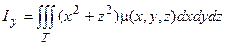, (1.8)

.

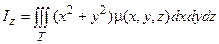Моменты инерции тела относительно координатных плоскостей xОy, yОz, xOz вычисляются по формулам:

, , .

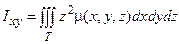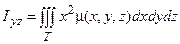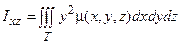5. Геометрические моменты инерции

Чтобы найти геометрические моменты инерции, используют те же формулы, что и для обычных моментов инерции, только плотность тела полагают равной единице, т.е. μ(х, у, z) = 1.

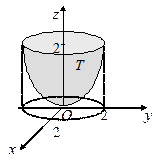Пример 1.3.Найти моменты инерции относительно координатных осей однородного тела (μ = const), ограниченного параболоидом x² + y² = 2z и плоскостью z = 2.

Решение. Для нахождения моментов инерции воспользуемся формулами (1.8).

Рис. 1.16

Так как проекцией области Т на плоскость xOy является круг, то вычисления удобнее проводить в цилиндрических координатах. Уравнение параболоида в новых координатах:

x² + y²=2z Þ ρ²cos²φ + ρ²sin²φ = 2z Þ .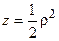

Область интегрирования Т можно задать следующими неравенствами: , , 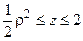. Вычислим тройные интегралы, используя формулу (1.6).

= .

= .

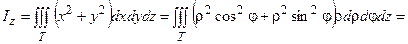
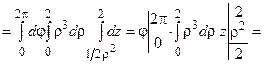
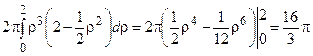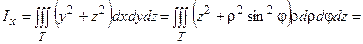
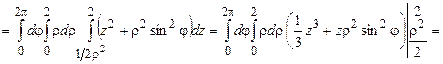
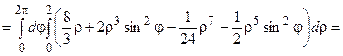
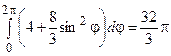Так как тело симметрично относительно оси Oz, то моменты инерции относительно осей Ох и Оу равны.

Ответ: моменты инерции тела: , .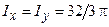

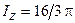Пример 1.4. Вычислить массу тела, ограниченного плоскостью z = 0 и полусферой 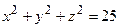( 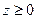), и имеющего пространственную плотность

.

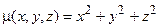Рис. 1.17

Решение. Массу тела будем вычислять с помощью тройного интеграла (1.5). Вычисления удобнее проводить в сферических координатах. Найдем уравнение плотности в новых координатах:

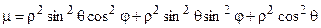Þ m = r².

В области интегрирования Т координаты r, j и q изменяются в пределах: , , 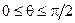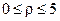. Следовательно, по формуле (1.7) масса равна

= .

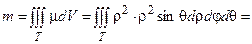
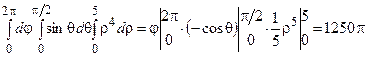Ответ: масса тела 1250p.

КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ

КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ

ПЕРВОГО РОДА

Рис. 2.1

Пусть в пространстве имеется некоторая гладкая кривая АВ, в каждой точке которой задана непрерывная функция f(x,y,z) (рис. 2.1). Пусть {l_i} - произвольное разбиение кривой АВ на n частей. Выберем в каждой дуге произвольным образом точку M_i и составим сумму

. (2.1)

Определение.Предел интегральных сумм (2.1) при стремлении максимального диаметра разбиения к нулю называется криволинейным интегралом первого рода от функции f по кривой АВ и обозначается

.

Таким образом, .

Криволинейный интеграл первого рода также называют криволинейным интегралом по длине дуги или от скалярной функции.

Необходимо отметить, что криволинейный интеграл первого рода не зависит от направления кривой АВ. Обычный определенный интеграл является частным случаем криволинейного, когда кривая интегрирования совпадает с осью Ox.