Биения. Сложение перпендикулярных колебаний. Затухающие механические колебания.
Биения - колебания с периодически меняющейся амплитудой, возникающие в результате наложения двух гармонических колебаний с несклько различными, но близкими частотами. Б. возникают вследствие того, что разность фаз между двумя колебаниями с различными частотами всё время изменяется так, что оба колебания оказываются в какой-то момент времени в фазе, через некоторое время - в противофазе, затем снова в фазе и т.д.
Пусть складывается два колебания с почти одинаковыми частотами, т.е.
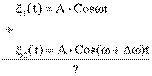 ,
, 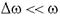 .
.
Из тригонометрии: 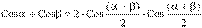 .
.
Применяя к нашему случаю, получим:
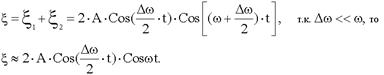
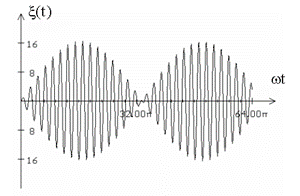
График результирующего колебания - график биений, т.е. почти гармонических колебаний частоты ω, амплитуда которых медленно меняется с частотойΔω .
Амплитуда 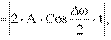 из-за наличия знака модуля (амплитуда всегда > 0) частота с которой изменяется амплитуда, равна не Δω / 2 , а в два раза выше - Δω.
из-за наличия знака модуля (амплитуда всегда > 0) частота с которой изменяется амплитуда, равна не Δω / 2 , а в два раза выше - Δω.
Сложение взаимно-перпендикулярных колебаний. Рассмотрим колебательную систему, состоящую из точечного груза массы 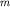 и четырех связанных с ним пружин.
и четырех связанных с ним пружин.
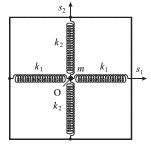
Мгновенное расположение точки m описывается двумя смещениями из положения равновесия - точки О: 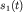 и
и 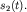 Такая система обладает двумя степенями свободы. Будем считать смещения малыми. При таких условиях колебания в двух взаимно перпендикулярных направлениях происходят независимо друг от друга:
Такая система обладает двумя степенями свободы. Будем считать смещения малыми. При таких условиях колебания в двух взаимно перпендикулярных направлениях происходят независимо друг от друга:

Здесь собственные частоты гармонических колебаний равны
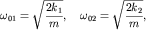
Рассмотрим вначале движение груза, если 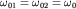 (жесткости всех пружин одинаковы).
(жесткости всех пружин одинаковы). 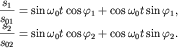
Умножим первое уравнение на 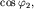 а второе - на
а второе - на 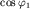 и вычтем второе уравнение из первого. В результате получим
и вычтем второе уравнение из первого. В результате получим
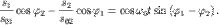
Теперь умножим первое уравнение на 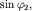 а второе - на
а второе - на 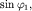 повторим вычитание и получим
повторим вычитание и получим
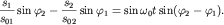
Наконец, возведем в квадрат каждое из равенств и сложим их. В результате время будет исключено, а уравнение траектории движущегося груза будет уравнением эллипса: 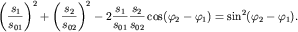
Направление движения вдоль траектории и ориентация эллипса относительно осей Os1 и Os2 зависят от начальной разности фаз 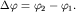 На рис. 1.8 изображены траектории движения груза при различных значениях
На рис. 1.8 изображены траектории движения груза при различных значениях 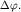
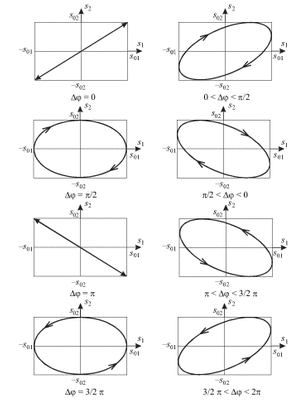
Если частоты двух взаимно-перпендикулярных колебаний не совпадают, но являются кратными: 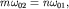 где
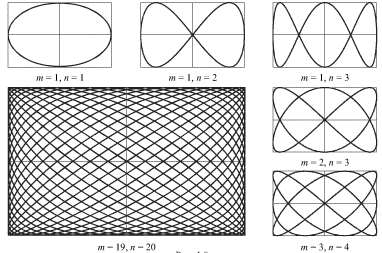
где 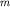 и
и  - целые числа, то траектории движения представляют собой замкнутые кривые, называемые фигурами Лиссажу (рис. 1.9). Отметим, что отношение частот колебаний равно отношению чисел точек касания фигуры Лиссажу к сторонам прямоугольника, в который она вписана.
- целые числа, то траектории движения представляют собой замкнутые кривые, называемые фигурами Лиссажу (рис. 1.9). Отметим, что отношение частот колебаний равно отношению чисел точек касания фигуры Лиссажу к сторонам прямоугольника, в который она вписана.
Если кратность между частотами отсутствует, то траектории не являются замкнутыми и постепенно заполняют весь прямоугольник, напоминая нить в клубке.
Затухающие механические колебания.Затухающие колебания – колебания, происходящие в присутствии внешних сил. Амплитуда уменьшается. Сила трения меняется по закону:
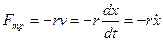
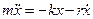
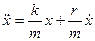
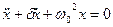 - дифференциальное уравнение затухающих колебаний
- дифференциальное уравнение затухающих колебаний
где, 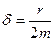 -коэфициент затухания.
-коэфициент затухания.
Амплитуда затухающих колебаний меняется по закону
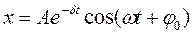
Частота не меняется.
